I. Объяснение нового материала.

О симметрии в пространстве учащиеся могут прочитать самостоятельно (п. 35).

Далее ввести понятие правильного многогранника. (Рассматривая куб, правильный тетраэдр, правильный октаэдр и т. д., учащиеся отвечают на вопрос: по каким признакам можно объединить данные многогранники?) Установить вместе с учащимися, сколько может быть видов правильных многогранников?

Пусть при одной вершине сходится n ребер, тогда плоских углов при этой вершине будет тоже n, причем они все равны между собой. Пусть один из этих плоских углов равен х, тогда сумма плоских углов при вершине nx, и по свойству плоских углов многогранного угла получим nx < 360°, откуда x < 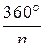(1).

Угол правильного n-угольника равен α = 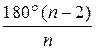(2).

I. Таблица значений						II. Таблица значений
	3	4	5	6	7		3	4	5	6
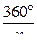
	120°	90°	72°	60°	≈ 51°		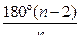60°	90°	108°	120°

Начиная с n = 7 плоский угол станет меньше 60°, а такого правильного многоугольника не существует, поэтому остальные случаи рассматривать не будем.

I. Грани правильного многогранника – правильные треугольники, тогда α = 60° (таблица II).

1) 60° ∙ 3 = 180° < 360°.

В этом случае правильный многогранник имеет 4 грани и называется правильным тетраэдром.

2) 60° ∙ 4 = 240° < 360°.

В этом случае правильный многогранник имеет 8 граней и называется правильным октаэдром.

3) 60° ∙ 5 = 300° < 360°.

В этом случае правильный многогранник имеет 20 граней и называется правильным икосаэдром.

4) 60° ∙ 6 = 360°, это противоречит теореме о сумме плоских углов многогранного угла. Следовательно, больше правильных многогранников, грани которых – правильные треугольники, не существует.

II. Грани правильного многогранника – правильные четырехугольники (квадраты),тогда α = 90° (таблица II).

1) 90° ∙ 3 = 270° < 360°.

В этом случае правильный многогранник имеет 6 граней и называется правильным гексаэдром (кубом).

2) 90° ∙ 4 = 360°, следовательно, больше правильных многогранников, грани которых – квадраты, не существует.

III. Грани правильного многогранника – правильные пятиугольники; α = 108°.

1) 108° ∙ 3 = 324° < 360°.

В этом случае правильный многогранник имеет 12 граней, и называется правильным додекаэдром.

2) 108° ∙ 4 > 360°, следовательно, больше правильных многогранников, грани которых – правильные пятиугольники, не существует.

IV. Начиная с правильного шестиугольника α ≥ 120° (таблица II).

Следовательно, nα > 360° (n ≥ 3), поэтому правильных многогранников, грани которых – многоугольники с числом сторон больше 5, не существует.

Во время беседы демонстрировать модели правильных многогранников, показывать рисунки (есть в параграфе).

Последний пункт объяснения нового материала – элементы симметрии правильных многогранников.

II. Решение задач: №№ 279, 280, 281, 282, 287.

Домашнее задание: теория (п. 35–37), №№ 283, 285, 286.

Урок 12
ПОДГОТОВКА К КОНТРОЛЬНОЙ РАБОТЕ

Ход урока

Вариант I

1. В основании прямого параллелепипеда ABCDA₁B₁C₁D₁ лежит ромб ABCD со стороной а, и углом BAD, равным 60°. Плоскость ВС₁D составляет с плоскостью основания угол 60°. Найдите площадь полной поверхности параллелепипеда.

2. В основании пирамиды DABC лежит прямоугольный треугольник АВС, С = 90°, А = 30°, ВС = 10. Боковые ребра пирамиды равно наклонены к плоскости основания. Высота пирамиды равна 5. Найдите площадь боковой поверхности пирамиды.

3*. В указанной выше пирамиде найдите угол между прямыми АС и BD.

Вариант II

1. Основанием прямого параллелепипеда служит параллелограмм со сторонами 3 см и 5 см. Острый угол параллелограмма равен 60°. Площадь большего диагонального сечения равна 63 см². Найдите площадь полной поверхности параллелепипеда.

2. Основанием пирамиды MABCD служит ромб ABCD, АС = 8; BD = 6. Высота пирамиды равна 1. Все двугранные углы при основании равны. Найдите площадь полной поверхности пирамиды.

3*. В указанной выше пирамиде найдите угол между гранями ВМС и DMC.

Вариант III

1. В основании прямого параллелепипеда ABCDA₁B₁C₁D₁ лежит параллелограмм ABCD, у которого BD АВ; AB = 3 см; BD = 4 см. Плоскость АВ₁С₁ составляет с плоскостью основания угол 45°. Найдите площадь полной поверхности параллелепипеда.

2. В основании пирамиды MABCD лежит квадрат ABCD со стороной, равной 12. Грани МВА и МВС перпендикулярны к плоскости основания. Высота пирамиды равна 5. Найдите площадь полной поверхности пирамиды.

3*. В указанной выше пирамиде найдите расстояние между прямыми ВС и MD.

Вариант IV

1. В прямом параллелепипеде ABCDA₁B₁C₁D₁ основанием служит параллелограмм ABCD, AD = 2, DC = 2 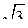, А = 30°. Большая диагональ составляет с плоскостью основания угол 45°. Найдите площадь боковой поверхности параллелепипеда.

2. Основанием пирамиды МАВС служит прямоугольный треугольник АВС, катеты которого АС = 8 см, ВС = 6 см. Высота пирамиды равна 3 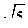см. Двугранные углы при основании пирамиды равны между собой. Найдите площадь полной поверхности пирамиды.

3*. В указанном выше параллелепипеде найдите угол между А₁С и плоскостью грани DD₁C₁C.

Домашняя контрольная работа

Вариант I

1. Сторона основания правильной четырехугольной призмы ABCDA₁B₁C₁D₁ равна 4 см, а боковое ребро – 5 см. Найдите площадь сечения, которое проходит через ребро АА₁ и вершину С.

2. В правильной треугольной призме сторона основания равна 3 см, а диагональ боковой грани составляет с плоскостью основания угол 60°. Площадь боковой поверхности призмы равна…

3. В наклонном параллелепипеде основанием служит квадрат. Две противоположные боковые грани перпендикулярны к плоскости основания. Все ребра параллелепипеда равны 4 см. Найдите площадь каждой из наклонных боковых граней.

4. В наклонной треугольной призме ABCA₁B₁C₁основанием служит правильный треугольник со стороной, равной а. Боковое ребро равно b, А₁АС = А₁АВ. Площадь грани СС₁В₁В равна…

5. В наклонной треугольной призме боковое ребро равно 10 см. Площади двух боковых граней равны 30 см² и 40 см², угол между ними прямой. Площадь боковой поверхности призмы равна…

6. В правильной четырехугольной пирамиде угол между диагональю основания и скрещивающимся с ней боковым ребром равен…

7. В правильной четырехугольной пирамиде угол между противоположными боковыми гранями равен 40°. Найдите угол наклона боковых граней к плоскости основания.

8. Основанием пирамиды служит треугольник со стороной, равной 8 см, и противолежащим углом 150°. Боковые ребра наклонены к основанию под углом 45°. Высота пирамиды равна…

9. Основанием пирамиды служит трапеция, основания которой равны 2 см и 8 см. Боковые грани пирамиды равно наклонены к плоскости основания. Высота одной из боковых граней равна 10 см. Найдите площадь боковой поверхности пирамиды.

10. В пирамиде MABCD основанием служит квадрат со стороной, равной а. Грань МАВ – правильный треугольник, плоскость которого перпендикулярна к плоскости основания. Площади граней MAD и МВС равны…

Вариант II

1. Сторона основания правильной четырехугольной призмы ABCDA₁B₁C₁D₁ равна 3 см, а боковое ребро – 4 см. Найдите площадь сечения, которое проходит через сторону основания АD и вершину С₁.

2. В правильной треугольной призме боковое ребро равно 4 см, а диагональ боковой грани составляет с плоскостью основания угол 45°. Площадь боковой поверхности призмы равна…

3. В наклонном параллелепипеде основанием служит квадрат. Две противоположные боковые грани перпендикулярны к плоскости основания. Все ребра параллелепипеда равны между собой. Площадь наклонной боковой грани равна 25 см². Длина ребра параллелепипеда равна…

4. Основанием наклонного параллелепипеда ABCDA₁B₁C₁D₁ служит квадрат со стороной, равной а. Боковое ребро равно b. Вершина А₁ равноудалена от всех вершин нижнего основания. Площадь диагонального сечения ВВ₁D₁D равна…

5. В наклонной треугольной призме боковое ребро равно 5 см. Площади двух боковых граней равны 20 см², угол между ними – 60°. Площадь боковой поверхности призмы равна…

6. В правильной треугольной пирамиде угол между скрещивающимися ребрами равен…

7. В правильной четырехугольной пирамиде боковые грани наклонены к основанию под углом 50°. Угол между противоположными боковыми гранями пирамиды равен…

8. В пирамиде основанием служит треугольник со стороной 6 см и противолежащим углом 30°. Боковые ребра наклонены к основанию под углом 60°. Длина бокового ребра равна…

9. Основанием пирамиды служит трапеция, боковые стороны которой равны 2 см и 4 см. Боковые грани пирамиды равно наклонены к плоскости основания. Высота одной из боковых граней равна 5 см. Найдите площадь боковой поверхности пирамиды.

10. В пирамиде MABCD основанием служит квадрат со стороной, равной 6 см. Ребро МВ перпендикулярно к плоскости основания. Равные боковые ребра равны 8 см. Площадь наклонных боковых граней равна…

Урок 13
КОНТРОЛЬНАЯ РАБОТА № 4

Вариант I

1. Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а. Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площадь боковой поверхности пирамиды.

2. Основанием прямого параллелепипеда ABCDA₁B₁C₁D₁ является ромб ABCD, сторона которого равна а и угол равен 60°. Плоскость AD₁C₁ составляет с плоскостью основания угол в 60°. Найдите:

а) высоту ромба;

б) высоту параллелепипеда;

в) площадь боковой поверхности параллелепипеда;

г) площадь поверхности параллелепипеда.

Вариант II

1. Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD = DM = a. Найдите площадь поверхности пирамиды.

2. Основанием прямого параллелепипеда ABCDA₁B₁C₁D₁ является параллелограмм ABCD, стороны которого равны а 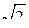и 2а, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:

а) меньшую высоту параллелограмма;

б) угол между плоскостью АВС₁ и плоскостью основания;

в) площадь боковой поверхности параллелепипеда;

г) площадь поверхности параллелепипеда.

Дата добавления: 2018-09-20; просмотров: 1033; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 10 11 12 13 14 15 16 171819 Следующая ⇒

Мы поможем в написании ваших работ!