III. Объяснение нового материала.
Выставить на стол как можно больше параллелепипедов (прямых, наклонных, прямоугольных, кубов) разных размеров и цветов.
Попросить одного ученика убрать со стола все наклонные параллелепипеды, оставить только прямые.
Далее из оставшихся прямых параллелепипедов убрать те, в основании которых не лежит прямоугольник.
Все оставшиеся – это прямоугольные параллелепипеды (в том числе и кубы).
Какой параллелепипед называется прямоугольным? (Прямой, в основании которого лежит прямоугольник.) Сформулировать определение, доказать свойства прямоугольного параллелепипеда, используя для их открытия аналогию с прямоугольником.
| В прямоугольнике все углы прямые. В прямоугольнике диагонали равны. В прямоугольнике квадрат диагонали равен сумме квадратов его сторон (d2 = a2 + b2) | В прямоугольном паралле- лепипеде все двугранные углы прямые. … … |
Рассмотреть куб как прямоугольный параллелепипед, у которого все три основания равны.
IV. Решение задач: №№ 187 (а), 188, 193, 195.
Домашнее задание: теория (п. 24), №№ 187 (б, в), 189, 191, 192, 217.
Урок 20
ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД
Цель : сформировать навык решения задач по изученной теме.
Ход урока
См. Крамор В. С. «Повторяем и систематизируем школьный курс геометрии». – М.: Просвещение, 1993.
А
1. Измерения прямоугольного параллелепипеда равны 6, 4 и 12 м. Найдите диагональ параллелепипеда. (Ответ: 14 м.)
2. Измерения комнаты равны 6, 8 и 3 м. Найдите площадь всех ее стен, пола и потолка. (Ответ: 180 м2.)
3. Площадь полной поверхности прямоугольного параллелепипеда равна 352 м2. Найдите его измерения, если они относятся как 1 : 2 : 3.
(Ответ: 4 м, 8 м и 12 м.)
4. В прямоугольном параллелепипеде стороны основания относятся как 7 : 24, а площадь диагонального сечения равна 50 м2. Найдите площадь боковой поверхности. (Ответ: 124 м2.)
В
1. Площадь диагонального сечения куба равна k. Найдите ребро куба, диагональ основания, диагональ куба, площадь его полной поверхности.
(Ответ: 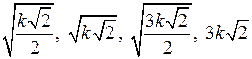 .)
.)
2. Диагональ прямоугольного параллелепипеда равна k и составляет с плоскостью основания угол α, а с большей боковой гранью угол β. Найдите площадь боковой поверхности параллелепипеда.
(Ответ: 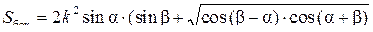 .)
.)
С
1. Диагональ прямоугольного параллелепипеда образует с меньшей боковой гранью угол β. Через большие стороны верхнего и нижнего оснований проведено сечение, образующее с плоскостью основания угол α. Зная, что периметр этого сечения равен Р, найдите измерения параллелепипеда. (Ответ: большая сторона 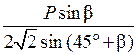 , меньшая сторона
, меньшая сторона 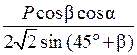 , H =
, H = 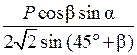 .)
.)
2. Диагональная плоскость прямоугольного параллелепипеда и лежащая в ней диагональ k образуют с одной и той же боковой гранью соответственно углы α и β. Найдите измерения параллелепипеда.
(Ответ: k sin β, k sin β ctg α, 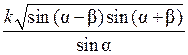 α, β – острые углы.)
α, β – острые углы.)
Урок 21
ПОДГОТОВКА К КОНТРОЛЬНОЙ РАБОТЕ
Ход урока
Вариант I
1. В треугольнике АВС АС = СВ = 10 см, 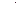 А = 30°, ВK – перпендикуляр к плоскости треугольника и равен 5
А = 30°, ВK – перпендикуляр к плоскости треугольника и равен 5 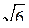 см. Найдите расстояние от точки K до АС.
см. Найдите расстояние от точки K до АС.
2. Точка М равноудалена от всех вершин равнобедренного прямоугольного треугольника АСВ ( 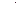 С = 90°), АС = ВС = 4 см. Расстояние от точки М до плоскости треугольника равно 2
С = 90°), АС = ВС = 4 см. Расстояние от точки М до плоскости треугольника равно 2 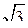 см.
см.
1) Докажите, что плоскость АМВ перпендикулярна плоскости АВС.
2) Какой угол плоскость ВМС составляет с плоскостью АВС?
3) Найдите угол между МС и плоскостью АВС.
3*. Найдите расстояние от точки Е – середины стороны АВ – до плоскости ВМС.
Вариант II
1. Через сторону АС треугольника АВС проведена плоскость α, удаленная от вершины В на расстояние, равное 4 см, АС = ВС = 8 см, 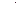 АВС =
АВС =
= 22°30′. Найдите угол между плоскостями АВС и α.
2. ABCD – квадрат со стороной, равной 4 см. Треугольник АМВ имеет общую сторону АВ с квадратом, АМ = ВМ = 2 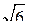 см. Плоскости треугольника и квадрата взаимно перпендикулярны.
см. Плоскости треугольника и квадрата взаимно перпендикулярны.
1) Докажите, что ВС 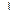 АМ.
АМ.
2) Найдите угол между МС и плоскостью квадрата.
3*. Найдите расстояние от точки А до плоскости DMC.
Вариант III
1. ABCD – ромб со стороной 4 см, 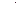 ADC = 150°, ВМ – перпендикуляр к плоскости ромба и равен 2
ADC = 150°, ВМ – перпендикуляр к плоскости ромба и равен 2 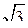 см. Найдите расстояние от точки М до AD.
см. Найдите расстояние от точки М до AD.
2. Точка М равноудалена от всех сторон правильного треугольника АВС, сторона которого равна 4 см. Расстояние от точки М до плоскости АВС равно 2 см.
1) Докажите, что плоскость АМО перпендикулярна плоскости ВМС (О – основание перпендикуляра, опущенного из точки М на плоскость АВС).
2) Найдите угол между плоскостью ВМС и плоскостью АВС.
3) Найдите угол между МС и плоскостью АВС.
3*. Точка Е принадлежит АС, причем АЕ : ЕС = 2 : 1. Найдите расстояние от точки Е до плоскости ВМС.
Вариант IV
1. Через сторону AD ромба ABCD проведена плоскость α, удаленная от ВС на расстояние, равное 3 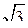 см. Сторона ромба – 12 см,
см. Сторона ромба – 12 см, 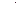 BCD = 30°. Найдите угол между плоскостью ромба и плоскостью α.
BCD = 30°. Найдите угол между плоскостью ромба и плоскостью α.
2. Треугольник АСВ – прямоугольный ( 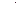 С = 90°), АС = СВ = 3 см. Треугольник АМС имеет общую сторону АС с треугольником АСВ; АМ = СМ =
С = 90°), АС = СВ = 3 см. Треугольник АМС имеет общую сторону АС с треугольником АСВ; АМ = СМ = 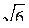 см. Плоскости треугольников взаимно перпендикулярны.
см. Плоскости треугольников взаимно перпендикулярны.
1) Докажите, что МС 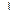 ВС.
ВС.
2) Найдите угол между МВ и плоскостью АВС.
3*. Найдите расстояние от середины АВ – точки Е – до плоскости ВМС.
Домашнее задание: карточки.
Вариант I
1. АВ  α; CD
α; CD  α; В
α; В  α, D
α, D  α; АВ = CD. Каково взаимное расположение прямой АС и плоскости α?
α; АВ = CD. Каково взаимное расположение прямой АС и плоскости α?
2. К плоскости проведены равные наклонные. Равны ли их проекции?
3. Точка М равноудалена от всех вершин прямоугольного треугольника, катеты которого 6 см и 8 см. Расстояние от точки М до плоскости треугольника равно 12 см. Найдите расстояние от точки М до вершин треугольника.
4. Основанием прямоугольного параллелепипеда является квадрат со стороной, равной а. Расстояние от бокового ребра до скрещивающейся с ним диагонали параллелепипеда равно…
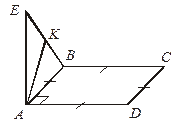 Рис. 1
Рис. 1
| 5. На рисунке 1 ABCD – квадрат. АЕ – перпендикуляр к плоскости квадрата. K  ЕВ. Чему равен угол между ВС и АK?
6. В треугольнике АВС АВ = 10; ЕВ. Чему равен угол между ВС и АK?
6. В треугольнике АВС АВ = 10;  А = 30°, BD А = 30°, BD 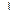 АВС, BD = 12. Расстояние от точки D до АС равно… АВС, BD = 12. Расстояние от точки D до АС равно…
|
7. Основанием прямоугольного параллелепипеда служит квадрат со стороной, равной 4. Диагональ параллелепипеда равна 8. Угол между диагональю и боковой гранью равен…
8. Точка М равноудалена от всех сторон квадрата ABCD, сторона которого равна 8 см. Расстояние от точки М до плоскости квадрата равно 4 см. Угол между плоскостью (MCD) и плоскостью квадрата равен…
9. Прямая а и плоскость α перпендикулярны плоскости β. Каково взаимное расположение прямой а и плоскости α?
10. Треугольник МАВ и квадрат ABCD имеют общую сторону АВ, и их плоскости взаимно перпендикулярны. Угол MAD равен…
Вариант II
1. АВ 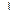 α, CD || АВ (B
α, CD || АВ (B  α, D
α, D  α), Е
α), Е  α,
α,  ECD = 40°. Тогда
ECD = 40°. Тогда  CED равен…
CED равен…
2. Две наклонные, проведенные к плоскости, имеют равные проекции. Равны ли сами наклонные?
3. Точка D равноудалена от всех вершин правильного треугольника и находится на расстоянии 3 см от его плоскости. Высота треугольника равна 6 см. Расстояние от точки D до вершин треугольника равно…
4. Основанием прямоугольного параллелепипеда служит квадрат со стороной, равной а. Расстояние между скрещивающимися диагоналями противоположных граней параллелепипеда равно…
 Рис. 2
Рис. 2
| 5. На рисунке 2 ABCD – квадрат. АЕ – перпендикуляр к плоскости квадрата, М  ЕС. Угол между BD и АМ равен…
6. В треугольнике АВС АВ = 16 см, ЕС. Угол между BD и АМ равен…
6. В треугольнике АВС АВ = 16 см,  А = = 30°, ВK – перпендикуляр к плоскости треугольника. Найдите ВK, если расстояние от точки K до АС равно 17 см. А = = 30°, ВK – перпендикуляр к плоскости треугольника. Найдите ВK, если расстояние от точки K до АС равно 17 см.
|
7. В прямоугольном параллелепипеде основанием служит квадрат. Диагональ параллелепипеда равна 10 см и составляет с плоскостью боковой грани угол 60°. Найдите стороны основания.
8. Точка D равноудалена от всех сторон правильного треугольника АВС. Расстояние от точки D до плоскости треугольника равно 2 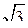 . Радиус описанной около треугольника окружности равен 4. Угол между плоскостью CDB и плоскостью треугольника равен…
. Радиус описанной около треугольника окружности равен 4. Угол между плоскостью CDB и плоскостью треугольника равен…
9. Две плоскости перпендикулярны к третьей. Линии пересечения этих плоскостей с третьей плоскостью параллельны. Каково взаимное положение этих плоскостей?
10. Прямоугольный треугольник АСВ (  С = 90°) и треугольник CMB имеют общую сторону ВС. Плоскости треугольников взаимно перпендикулярны. Угол АСМ равен…
С = 90°) и треугольник CMB имеют общую сторону ВС. Плоскости треугольников взаимно перпендикулярны. Угол АСМ равен…
Дата добавления: 2018-09-20; просмотров: 997; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
