II. Объяснение нового материала.
Как проверить перпендикулярность данной прямой к данной плоскости? Исходя из определения, необходимо проверить перпендикулярность данной прямой по отношению к любой прямой, лежащей в плоскости. Но таких прямых – бесконечно много. Сколько достаточно взять, чтобы ответить на данный вопрос?

| Начнем с наименьшего количества прямых. Возьмем одну прямую, лежащую в плоскости. (Учитель демонстрирует.) Видно, что одной прямой недостаточно. |
Возьмем две прямые. Две прямые на плоскости могут быть параллельными или пересекающимися.

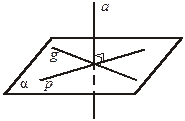
Что вы замечаете? Сформулируйте признак перпендикулярности прямой и плоскости.
Признак формулируется. Записываются условия и требования. Что надо доказать, чтобы утверждать, что прямая а перпендикулярна плоскостиα? (Что прямая а перпендикулярна любой прямой, лежащей в этой плоскости.)
Далее работа с учащимися строится по плану:
1) прочитать доказательство признака перпендикулярности прямой и плоскости (п. 17);
2) сделать чертеж;
3) оформить доказательство.
III. Решение задач.
№ 127.

| Дано: Δ АВС,  А + А +  В = 90°, BD В = 90°, BD  (АВС).
Доказать, что CD (АВС).
Доказать, что CD  АС.
Доказательство
1. АС.
Доказательство
1. 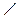 А + А +  В = 90° В = 90° 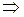  С = 90°. С = 90°.
|
2. 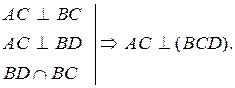
3. 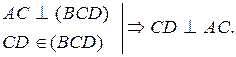
№ 128.
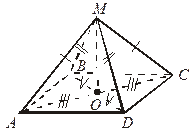
| Дано: ABCD – параллелограмм, АМ = МС, ВМ = МD.
Доказать, что МО  (АВС). (АВС).
|
Доказательство
1. 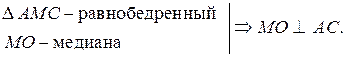
2. 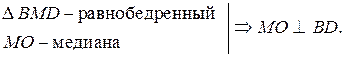
3. 
№ 130.
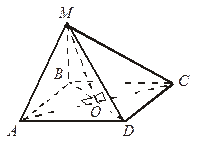
| Дано:  МВА = МВА = 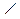 МВС = 90°, МВ = m, АВ = n.
Найдите: АМ, СМ, DM; расстояние от М до АС и BD. МВС = 90°, МВ = m, АВ = n.
Найдите: АМ, СМ, DM; расстояние от М до АС и BD.
|
Решение
1. 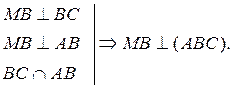
2. AM = CM = 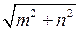 .
.
3. ρ (M, BD) = MB = m.
|
|
|
4. ρ (M, AC) – ?
а) 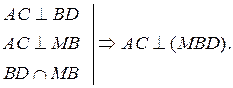
б) 
ρ (M, AC) = MO, MO = 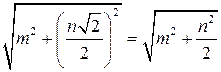 .
.
Домашнее задание: теория (п. 17), №№ 129, 131.
Урок 4
ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ
ПРЯМОЙ И ПЛОСКОСТИ
Цель : сформировать навык применения признака перпендикулярности прямой и плоскости к решению задач.
Ход урока
I. Проверка домашнего задания (теорема, №№ 129, 131).
II. Устная работа.
1. Можно ли утверждать, что прямая, проходящая через центр круга перпендикулярна:
а) диаметру;
б) двум радиусам;
в) двум диаметрам, перпендикулярна плоскости круга?
(а) нет; б) нет; в) да.)
2. Можно ли утверждать, что прямая перпендикулярна плоскости, если она перпендикулярна лежащим в этой плоскости:
а) двум сторонам треугольника;
б) двум сторонам квадрата;
в) диагоналям параллелограмма.
3. Дано ABCD – куб. Заполните пропуски о взаимном расположении прямых и плоскостей:
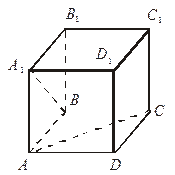
| а) СС1…(DCB); б) АА1…(DCB); в) D1C1…(DCB); г) В1С1…(DD1C1); д) В1С1…DC1; е) А1D1…DC1; ж) ВВ1…АС; з) А1В…ВС; и) А1В…DC1. |
4. Три луча ОМ, ON, ОК попарно перпендикулярны. Как расположен каждый из лучей по отношению к плоскости, определяемой двумя другими лучами?
Что моделирует в классной комнате описанную комбинацию?
III. Решение задач.

| 1. Дано: Е  (ABCD), ABCD – прямоугольник. ВЕ (ABCD), ABCD – прямоугольник. ВЕ  АВ, ВЕ АВ, ВЕ  ВС.
Доказать, что: а) ВЕ ВС.
Доказать, что: а) ВЕ  CD; б) CD CD; б) CD  (ВСЕ).
Найдите SECD, если CD = 6 см, CЕ = 8 см. (ВСЕ).
Найдите SECD, если CD = 6 см, CЕ = 8 см.
|

| 2. Дано: ABCD – тетраэдр, BD  ВС, DC ВС, DC  АС, АС,  АСВ = 90°.
Доказать, что АС ^ BD.
Найдите SABD, если AD = 25 см, АВ = 24 см. АСВ = 90°.
Доказать, что АС ^ BD.
Найдите SABD, если AD = 25 см, АВ = 24 см.
|

| 3. Дано: ABCD – тетраэдр. AD  АС, AD АС, AD  АВ, DC АВ, DC  СВ.
Доказать, что: а) AD СВ.
Доказать, что: а) AD  ВС; б) ВС ВС; б) ВС  (ADC).
Найдите SАВС, если ВС = 4 см, АС = 3 см. (ADC).
Найдите SАВС, если ВС = 4 см, АС = 3 см.
|
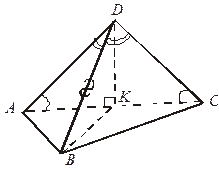
| 4. Дано: ABCD – тетраэдр.
 ADC = ADC =  BDC, BDC,
 ABD = ABD =  DAB.
Найдите DAB.
Найдите  (АВ, CD).
Решение
1. Δ ADB – равнобедренный (АВ, CD).
Решение
1. Δ ADB – равнобедренный   DK – высота и медиана. DK – высота и медиана.
|
2. Δ ADС = Δ ВDС (по двум сторонам и углу между ними)  АС = CB.
АС = CB.
|
|
|
3. 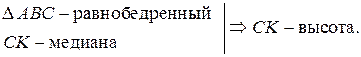
4. 
5. 
Урок 5
ТЕОРЕМА О ПЛОСКОСТИ, ПЕРПЕНДИКУЛЯРНОЙ ПРЯМОЙ.
ТЕОРЕМА О ПРЯМОЙ, ПЕРПЕНДИКУЛЯРНОЙ ПЛОСКОСТИ
Цель : доказать теоремы существования и единственности прямой (плоскости), перпендикулярной к данной плоскости (прямой).
Ход урока
Дата добавления: 2018-09-20; просмотров: 1093; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
