II. Объяснение нового материала.
Пункты учебника (п. 8, 9) можно прочитать вместе с учащимися. Проверить осознанность усвоения теоремы об углах с соноправленными сторонами, можно, попросив учащихся доказать теорему на видоизмененном чертеже, составить план доказательства.

III. Решение задач №№ 44, 45, 47.
Домашнее задание: теория (п. 8 – 9); №№ 46, 97.
Уроки 10–11
АКСИОМЫ СТЕРЕОМЕТРИИ.
ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ
Цель : повторить теорию, подготовить учащихся к контрольной работе.
Ход уроков
I. Устная работа.
1. Прямая пересекает две стороны треугольника. Лежит ли она в плоскости этого треугольника?
2. Прямая пересекает вершину треугольника. Лежит ли она в плоскости этого треугольника?
3. Три вершины параллелограмма лежат в плоскости. Принадлежит ли четвертая вершина параллелограмма этой плоскости?
4. Хорда окружности принадлежит плоскости. Верно ли утверждение, что и вся окружность лежит в этой плоскости?
5. Две пересекающиеся хорды окружности принадлежат плоскости. Верно ли утверждение, что любая точка окружности принадлежит этой плоскости?
6. Сколько плоскостей можно провести через: три различные точки; две различные точки; через прямую и не лежащую на ней точку; через две параллельные прямые?
7. Верно ли утверждение: любые три точки принадлежат плоскости; через любые три точки проходит единственная плоскость?
8. Известно, что прямая параллельна плоскости. Параллельна ли она любой прямой, лежащей в этой плоскости? Может ли данная прямая пересечь какую-либо прямую, лежащую в плоскости?
|
|
|
9. Средняя линия трапеции лежит в плоскости α. Пересекают ли основания трапеции эту плоскость?
10. Прямая а параллельна линии пересечения плоскостей α и β. Каково взаимное расположение а и α; а и β?
11. Прямая b непараллельна линии пересечения плоскостей α и β. Каково взаимное расположение b и α; b и β?
12. Сколько можно провести через данную точку: прямых, параллельных данной плоскости; плоскостей, параллельных данной прямой?
13. Стороны АВ и ВС параллелограмма ABCD пересекают некоторую плоскость. Докажите, что прямые AD и DC пересекают эту плоскость.
14. Плоскость αпараллельна одной из двух параллельных прямых. Каково взаимное расположение второй прямой и плоскости α?
15. Сторона АВ параллелограмма ABCD лежит в плоскости α.Докажите, что сторона CD параллельна этой плоскости.
16. Прямая пересекает плоскость. Можно ли в плоскости провести прямую, параллельную данной прямой?
17. Две прямые параллельны одной плоскости. Можно ли утверждать, что эти прямые параллельны?
18. Каким может быть взаимное расположение двух прямых, из которых одна параллельна некоторой плоскости, а другая пересекает эту плоскость?
|
|
|
19. Прямые а и b скрещиваются с прямой с. Могут ли прямые а и b быть параллельными? Пересекаться?
20. Может ли каждая из двух скрещивающихся прямых быть параллельна третьей прямой?
21. Прямая, не лежащая в плоскости параллелограмма, параллельна одной из его диагоналей. Каково взаимное расположение данной прямой и второй диагонали?
22. Как могут быть расположены прямая и плоскость, если данная прямая и некоторая прямая, лежащая в этой плоскости, скрещиваются?
II. Решение задач.
Варианты I и IV рассмотреть в классе. Варианты II и III дать домой для самостоятельного решения.
Вариант I
1. На рисунке точки А, С, М и Р лежат в плоскости α, а точка В 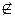 α.
Постройте точку пересечения прямой MP с плоскостью АВС.
Поясните. α.
Постройте точку пересечения прямой MP с плоскостью АВС.
Поясните.
| 
|
2. Треугольники АВС и ADC лежат в разных плоскостях и имеют общую сторону АС. Точка Е лежит на стороне АВ, F – на стороне ВС, причем EF параллельна плоскости ADC. Р – середина AD, а K – середина DC.
1) Докажите, что EF || PK.
2) Каково взаимное положение прямых РK и АВ? Чему равен угол между этими прямыми, если  АВС = 40° и
АВС = 40° и  ВСА = 80°?
ВСА = 80°?
3. Плоскости α и β пересекаются по прямой m. Прямая а лежит в плоскости α. Каково возможное взаимное положение прямой а и плоскости β? Сделайте рисунок и поясните.
|
|
|
4*. Используя рисунок, постройте линию пересечения плоскости EFM с плоскостью α. Поясните.
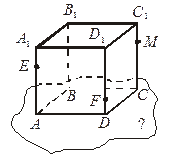
Вариант IV
1. На рисунке точки Е и F лежат в плоскости β, а М – в плоскости α. Постройте линии пересечения плоскости EFM с плоскостями α и β. Поясните.
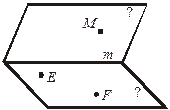
2. Основание AD трапеции ABCD лежит в плоскости α. Через точки В и С проведены параллельные прямые, пересекающие плоскость α в точках Е и F соответственно.
1) Докажите, что BCFE – параллелограмм.
2) Каково взаимное положение прямых EF и АВ? Чему равен угол между ними, если  АВС = 150°? Поясните.
АВС = 150°? Поясните.
3. Отрезок АВ параллелен плоскости α, а отрезок CD лежит в этой плоскости, причем AB = CD. Можно ли утверждать, что четырехугольник ABDC – параллелограмм? Поясните.
| 4*. Плоскости α и β пересекаются по прямой m. Прямая АВ лежит в плоскости α, а CD – в плоскости β. Что нужно изменить в условии, чтобы прямые АС и BD могли пересекаться? В каком случае это возможно? | 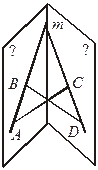
|
Вариант II
| 1. На рисунке точки А и В лежат в плоскости α, а С – в плоскости β. Постройте линии пересечения плоскости АВС с плоскостями α и β. Поясните. | 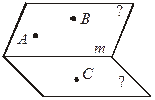
|
2. Треугольники ABC и DCE лежат в разных плоскостях и имеют общую вершину С, АВ || DE.
|
|
|
1) Постройте линию пересечения плоскостей АВС и DCE. Поясните.
2) Каково взаимное положение прямых АВ и DF, где F лежит на стороне CE? Чему равен угол между этими прямыми, если  FED = 60° и
FED = 60° и  DFE = 100°? Поясните.
DFE = 100°? Поясните.
3. Прямая а параллельна плоскости α, точка М и прямая с лежат в плоскости α (М  с). Через точку М проведена прямая b, параллельная а. Каково взаимное положение прямых b и с? Поясните.
с). Через точку М проведена прямая b, параллельная а. Каково взаимное положение прямых b и с? Поясните.
| 4*. Плоскости α и β пересекаются по прямой m. Прямая АВ лежит в плоскости α, а CD – в плоскости β. Что нужно изменить в условии, чтобы прямые EF и MK могли быть параллельными? Поясните. | 
|
Вариант III
1. На рисунке точки А, С, E и F лежат в плоскости α, а точка В  α.
Постройте точку пересечения прямой EF с плоскостью АВС.
Поясните. α.
Постройте точку пересечения прямой EF с плоскостью АВС.
Поясните.
| 
|
2. Трапеция ABCD (AD и ВС – основания) и треугольник AED имеют общую сторону AD и лежат в разных плоскостях. Точка М лежит на стороне АЕ, а Р – на стороне DE, причем МР параллельна плоскости трапеции.
1) Докажите, что МР || ВС.
2) Каково взаимное положение прямых МР и АВ? Чему равен угол между этими прямыми, если  АВС = 110°? Поясните.
АВС = 110°? Поясните.
3. Плоскости α и β пересекаются по прямой m. Прямая а лежит в плоскости α, а b – в плоскости β. Какие возможны взаимные положения прямых а и b? Сделайте рисунок и поясните.
| 4*. Используя рисунок, постройте линию пересечения плоскости МРK с плоскостью α. Поясните. | 
|
Урок 12
КОНТРОЛЬНАЯ РАБОТА № 1
Ход урока
Вариант I
1. В каком случае три точки в пространстве не определяют положение плоскости, проходящей через эти точки?
2. Могут ли две различные плоскости иметь только одну общую точку?
3. Точка М не лежит на прямой а. Через точку М проводятся прямые, пересекающие прямую а. Лежат ли эти прямые в одной плоскости?
4. Каково взаимное положение прямых: 1) AD1 и MN; 2) AD1 и ВС1; 3) MN и DC? (Рис. 1.)
5. Прямые а и b скрещиваются с прямой с. Могут ли прямые а и b пересекаться?
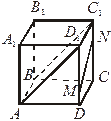


Рис. 1 Рис. 2 Рис. 3
6. Прямая а параллельна плоскости α. Существуют ли на плоскости α прямые, не параллельные а? Если да, то каково их взаимное положение?
7. На рисунке 2 прямые m и n пересекаются в точке М, А  m; В
m; В  n; b лежит в плоскости α, а || b. Каково взаимное положение прямых b и c?
n; b лежит в плоскости α, а || b. Каково взаимное положение прямых b и c?
8. Даны треугольник АВС и плоскость α, АВ || α; АС || α. Каково взаимное положение прямой ВС и плоскости α?
9. На рисунке 3 плоскости α и β параллельны. Пересекающиеся в точке М прямые а и b пересекают плоскость α в точках А и С, а плоскость β – в точках В и D,  . Найдите отношение
. Найдите отношение  .
.
10. Плоскость α пересекает только боковые ребра параллелепипеда. Определите вид сечения.
Вариант II
1. Что можно сказать о взаимном положении двух плоскостей, имеющих три общие точки, не лежащие на одной прямой?
2. Могут ли две различные плоскости иметь только две общие точки?
3. Прямые а и b пересекаются в точке М. Прямая с, не проходящая через точку М, пересекает прямые а и b. Лежат ли все эти три прямые в одной плоскости?
4. Каково взаимное положение прямых: 1) A1D и MN; 2) A1D и В1С; 3) MN и А1В1? (Рис. 1.)
5. Прямые а и b скрещиваются с прямой с. Могут ли прямые а и b быть параллельными?


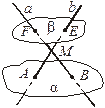
Рис. 1 Рис. 2 Рис. 3
6. Две прямые параллельны одной и той же плоскости. Можно ли утверждать, что эти прямые параллельны между собой? Если нет, то каково их взаимное положение?
7. На рисунке 2 прямые m и n параллельны. Точки А и В соответственно принадлежат прямым m и n; b лежит в плоскости α, а || b. Каково взаимное положение прямых b и с?
8. Даны четырехугольник АВСD и плоскость α. Его диагонали АС и BD параллельны плоскости α. Каково взаимное положение АВ и плоскости α?
9. На рисунке 3 плоскости α и β параллельны. Пересекающиеся в точке М прямые а и b пересекают плоскость α соответственно в точках В и А, а плоскость β – в точках Е и F. 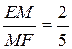 . Найдите отношение
. Найдите отношение  .
.
10. Плоскость α проходит через диагональ основания параллелепипеда и середину одной из сторон верхнего основания. Определите вид сечения.
Урок 13
ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ.
ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ДВУХ ПЛОСКОСТЕЙ
Цели : ввести понятие параллельных плоскостей; доказать признак параллельности двух плоскостей.
Ход урока
I. Объяснение нового материала построить в соответствии с пунктом 11 учебника.

| Дано: а  b = М, а b = М, а  α, b α, b  α,
а || а1, b || b1, а1 α,
а || а1, b || b1, а1  β, b1 β, b1  β.
Доказать, что α || β. β.
Доказать, что α || β.
|
Доказательство
1.  2.
2. 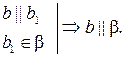
3. Пусть α  β, тогда α
β, тогда α  β = c.
β = c.
4.  5.
5. 
6. а || с, b || c, но а  b = М по условию.
b = М по условию.
Полученное противоречие доказывает, что наше предположение неверно. Следовательно, α || β.
II. Решение задач.
№ 48 (устно).
№ 49.

| Дано: m  α = В.
Существует ли β: m α = В.
Существует ли β: m  β, α || β?
1. m β, α || β?
1. m  α = В α = В  В В  α.
2. m α.
2. m  β β  В В  β. β.
|
3. 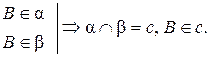
№ 50.

| Дано: α || β, m  α.
Доказать, что m || β.
Доказательство
1. Пусть m || β, m α.
Доказать, что m || β.
Доказательство
1. Пусть m || β, m  β = K. β = K.
|
2. 
Получили противоречие условию, которое опровергает наше предположение. Следовательно, m || β.
№ 54.

| Дано: В  (ADC), АМ = МВ,
CN = NB, BP = PD.
Доказать, что (MNP) || (АВС).
Найти SMNP, если SADC = 48 см2. (ADC), АМ = МВ,
CN = NB, BP = PD.
Доказать, что (MNP) || (АВС).
Найти SMNP, если SADC = 48 см2.
|
Решение
1. MN – средняя линия Δ АВС 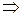 MN || AC.
MN || AC.
2. NP – средняя линия Δ CBD  NP || CD.
NP || CD.
3.  по признаку.
по признаку.
4. Δ MNP 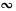 Δ ADC, K =
Δ ADC, K = 
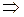 SMNP =
SMNP =  ∙ 48 = 12 (см2).
∙ 48 = 12 (см2).
Домашнее задание: теория (п. 10), №№ 51, 52, 53.
Урок 14
СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЕЙ
Цели : доказать теорему существования и единственности плоскости, параллельной данной и проходящей через данную точку пространства; рассмотреть свойства параллельных плоскостей.
Ход урока
I. Проверка домашнего задания (у доски).
II. Устная работа.
1. Верно ли, что если две пересекающиеся прямые, лежащие в одной плоскости, параллельны другой плоскости, то эти плоскости параллельны. (Верно.)
2. Верно ли, что если две прямые, лежащие в одной плоскости, параллельны двум прямым другой плоскости, то эти плоскости параллельны. (Нет. Привести контрпример – пересекающиеся плоскости, проведенные через параллельные прямые.)

| 3. Дано:  DAB + DAB +  AEP = 180°, AEP = 180°,
 DBC + DBC +  ТРВ = 180°.
Доказать, что (АВС) || (ЕРТ). ТРВ = 180°.
Доказать, что (АВС) || (ЕРТ).
|
4. Каким может быть взаимное расположение прямой а и плоскости β, если прямая а лежит в плоскости α, параллельной плоскости β?
5. Как могут быть расположены плоскости α и β, если плоскость α проходит через некоторую прямую а, параллельную плоскости β?
6. Как могут быть расположены плоскости α и β, если любая прямая, лежащая в плоскости α, параллельна плоскости β?
III. Объяснение нового материала построить как процесс решения задач в соответствии с пунктом 11 учебника.
IV. Решение задач: №№ 55, 56, 58, 59, 60.
№ 55.
Дано: а  α, β || α.
α, β || α.
Доказать, что а  β.
β.

| Доказательство
1. Проведем b: В  b, В b, В  β, b || а.
2. β, b || а.
2.  по лемме. по лемме.
|
№ 56. 
| Дано: α || β, А  α, А α, А  а, а || β.
Доказать, что а а, а || β.
Доказать, что а  α.
Доказательство
1. Пусть а α.
Доказательство
1. Пусть а 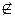 α, тогда а α, тогда а 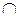 α = А. α = А.
|
2. 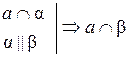 (задача № 55).
(задача № 55).
Получили противоречие условию. Следовательно, наше предположение неверно и а  α.
α.
№ 60.

| Дано: α || χ, β || χ.
Доказать, что α || β.
Доказательство
1. Проведем в плоскости α пересекающиеся прямые а и b.
2. Отметим С  χ. χ.
|
Проведем (а, С) = Q1, Q1  χ = а1. (b, С) = Q2, Q2
χ = а1. (b, С) = Q2, Q2  χ = b1.
χ = b1.
Причем а || а1 и b || b1, а1  b1 = c.
b1 = c.
3. Аналогично проведем рассуждения для плоскостей β и χ. Получим в плоскости β прямые а2 и b2. Причем а1 || а2, b1 || b2.
4.  по признаку.
по признаку.
Домашнее задание: теория (п. 11), №№ 57, 61, 104.
Урок 15
ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ.
СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЕЙ
Цель : сформировать навык применения изученных свойств параллельных плоскостей при решении задач.
Ход урока
I. Проверка домашнего задания (у доски).
II. Устная работа.
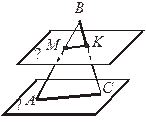
| 1. Дано: Δ АВС, АС  α, АМ = МВ, М α, АМ = МВ, М  β, β || α,β β, β || α,β  ВС = K.
Доказать, что МK – средняя линия Δ АВС. ВС = K.
Доказать, что МK – средняя линия Δ АВС.
|

| 2. Одна из сторон треугольника принадлежит плоскости α. Плоскость β параллельна плоскости α и пересекает две другие стороны треугольника. Доказать, что β отсекает от треугольника треугольник, подобный данному. |

| 3. Дано: (MNK) || (АВС).
Доказать, что  MNK = MNK =  АВС. АВС.
|

| 4. Дано: α || β, АА1 || ВВ1, АВ = 10 см. Найти А1В1. |

| 5. Дано: α || β, а  b = О, АО = ОС,DO = ОВ.
Определить вид четырехугольника ABCD. b = О, АО = ОС,DO = ОВ.
Определить вид четырехугольника ABCD.
|
III. Решение задач. №№ 63, 64, 65 (устно), 107.
Домашняя контрольная работа
Вариант I
1. Параллелограммы ABCD и ADFE лежат в разных плоскостях и имеют общую сторону AD. Прямая m, параллельная BC, пересекает плоскости АВЕ и DCF соответственно в точках Н и Р. Докажите, что HPFE – параллелограмм.
2. На рисунке 1 плоскости α и β параллельны, а || а1. Прямая а пересекает плоскости α и β соответственно в точках А и В, а прямая а1 пересекает плоскость α в точке А1. Постройте точку пересечения а1 с плоскостью β. Поясните.


Рис. 1 Рис. 2
3. В тетраэдре DABC  DBA =
DBA =  DBC = 90°, DB = 6, АВ = ВС = 8, АС = 12. Постройте сечение тетраэдра плоскостью, проходящей через середину DB и параллельной плоскости ADC. Найдите площадь сечения.
DBC = 90°, DB = 6, АВ = ВС = 8, АС = 12. Постройте сечение тетраэдра плоскостью, проходящей через середину DB и параллельной плоскости ADC. Найдите площадь сечения.
4*. Постройте сечение параллелепипеда плоскостью, проходящей через точки Е и F и параллельной прямой а (рис. 2).
Вариант II
1. Вне плоскости αрасположен треугольник АВС, у которого медианы АА1 и ВВ1 параллельны плоскости α. Через вершины В и С треугольника проведены параллельные прямые, которые пересекают плоскость α соответственно в точках Е и F. Докажите, что ECBF – параллелограмм.
2. На рисунке 1 плоскости α и β параллельны. Прямая а пересекает плоскости α и β соответственно в точках А и В, а прямая b – в точках С и D. Найдите взаимное положение прямых а и b. Поясните.


Рис. 1 Рис. 2
3. Все грани параллелепипеда ABCDA1B1C1D1 – квадраты со стороной а. Через середину AD параллельно плоскости DA1B1 проведена плоскость. Найдите периметр сечения.
4*. Постройте сечение тетраэдра плоскостью, проходящей через точки С и К и параллельной прямой а (рис. 2).
Вариант III
1. Прямоугольники ABCD и EBCF лежат в разных плоскостях и имеют общую сторону ВС. Прямая а параллельна AD и пересекает плоскости АВЕ и DCF соответственно в точках Р и Н. Докажите, что РВСН – параллелограмм.
2. На рисунке 1 плоскости α и β параллельны. Прямые а и b пересекаются в точке М. Прямая а пересекает плоскости α и β соответственно в точках А и В, а прямая b пересекает плоскость β в точке D. Постройте точку пересечения прямой b с плоскостью α.

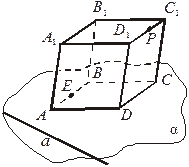
Рис. 1 Рис. 2
3. В тетраэдре DABC точка М – середина АС, DB = 6, MD = 10,
Ð DBM = 90°. Постройте сечение тетраэдра плоскостью, проходящей через середину ребра DC и параллельной плоскости DMB, и найдите площадь сечения.
4*. Постройте сечение параллелепипеда плоскостью, проходящей через точки Е и Р и параллельной прямой а (рис. 2).
Вариант IV
1. Трапеция ABCD (AD и ВС – основания) расположена вне плоскости α. Диагонали трапеции параллельны плоскости α. Через вершины А и В проведены параллельные прямые, которые пересекают плоскость α в точках Е и F соответственно. Докажите, что EABF – параллелограмм.
2. На рисунке 1 плоскости α и β параллельны. Прямая а пересекает плоскости α и β соответственно в точках А и В, а прямая b – в точках С и D. Каково взаимное положение прямых а и b? Поясните.


Рис. 1 Рис. 2
3. Дан параллелепипед ABCDA1B1C1D1, все грани которого – прямоугольники, AD = 4, DC = 8, СС1 = 6. Постройте сечение параллелепипеда плоскостью, проходящей через середину ребра DC и параллельной плоскости AB1C1, и найдите периметр сечения.
4*. Постройте сечение тетраэдра плоскостью, проходящей через точки С и М и параллельной прямой а (рис. 2).
Урок 16
ТЕТРАЭДР
Цель : ввести понятие тетраэдра, проиллюстрировать изученные понятия, связанные со взаимным расположением прямых и плоскостей на примере треугольной пирамиды.
Ход урока
I. Объяснение нового материала построить в соответствии с пунктом 12.
II. Решение задач: №№ 66, 67, 68 (на готовом чертеже), 69, 70, 74.
№ 69.

| Дано: SABC – тетраэдр.
МА = МВ, BN = NC, М  α, N α, N 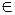 α, BS || α, α α, BS || α, α  (ABS) = PM, α (ABS) = PM, α  (BCS) = = KN.
Доказать, что РМ || KN. (BCS) = = KN.
Доказать, что РМ || KN.
|
Доказательство
1. 
2. 
3. 
№ 70.

| Дано: ABCD – тетраэдр, АМ = МВ, AN = ND, AK = KC. Доказать, что (MNK) || (BCD). |
Доказательство
1. MK || ВС (по свойству средней линии).
2. MN || BD (по свойству средней линии).
3. 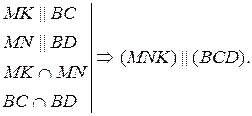 .
.
№ 74.

| Дано: ABCD – тетраэдр, О – точка пересечения медиан Δ BCD, О  α, α || (АВС), α α, α || (АВС), α  AD = М, α AD = М, α  ВD = K, α ВD = K, α  DС = N.
Доказать, что Δ MNK DС = N.
Доказать, что Δ MNK 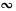 Δ АВС.
Найдите Δ АВС.
Найдите  . .
|
Решение
1. 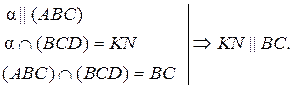
2. Аналогично MK || AB, MN || AC.
3. Δ BCD  Δ KND (по двум углам)
Δ KND (по двум углам)  KN =
KN =  BC, DK =
BC, DK =  BD,
BD,
DN =  DC.
DC.
4. 
5. Δ MDK  Δ ADB (по двум углам)
Δ ADB (по двум углам)  MK =
MK =  AB.
AB.
6. Аналогично, MN =  AC.
AC.
7. Δ MNK  Δ ABC (по трем сторонам).
Δ ABC (по трем сторонам).
8.  .
.
Домашнее задание: теория (п. 12), №№ 71, 102, 103.
Урок 17
ПАРАЛЛЕЛЕПИПЕД
Цель : ввести понятие параллелепипеда, рассмотреть свойства ребер, граней, диагоналей параллелепипеда.
Ход урока
I. Объяснение нового материала построить в соответствии с пунктом 13 учебника.
II. Решение задач: №№ 76 (устно), 77, 78 (устно по готовому чертежу), 79, 80.
III. Домашнее задание: теория (п. 13), №№ 81, 109, 110. Подготовить ответы на вопросы к главе I.
Урок 18
ЗАДАЧИ НА ПОСТРОЕНИЕ СЕЧЕНИЙ
Цель : сформировать навык решения простейших задач на построение сечений тетраэдра и параллелепипеда.
Ход урока
I. Устная работа – вопросы к главе I.
II. Решение задач: №№ 72, 73, 75, 82.
III. Домашнее задание: теория (п. 14), №№ 83, 84, 85, 86.
Дополнительно:
1. ABCD – тетраэдр, М – середина АС, DB = 6, MD = 10,  DBM = 90°.
DBM = 90°.

| Постройте сечение тетраэдра плоскостью, проходящей через середину DC параллельно плоскости (DMB), и найдите Sсеч.
1) MB = 8 см.
2) Δ DBM  Δ KNF, K = Δ KNF, K =  . .
|
SDBM = 24 см2  SKNF = 6 см2.
SKNF = 6 см2.
2. Все грани параллелепипеда – прямоугольники.

| AD = 4, DC = 8, СС1 = 6, М – середина DC. Постройте сечение параллелепипеда плоскостью, проходящей через М и параллельной (АВ1С1). Найти Рсеч. |
Урок 19
КОНТРОЛЬНАЯ РАБОТА № 2
Домашняя контрольная работа
1. Через точку K, не лежащую между параллельными плоскостями α и β, проведены прямые а и b. Прямая а пересекает плоскости α и β в точках А1 и А2соответственно, b – в точках В1 и В2.
| Найти В1В2, если А2В2 : А1В1 = = 9 : 4, КВ1 = 8 см. | Найти KВ2, если А1В1 : А2В2 = = 3 : 4, КВ1 = 14 см. |
| 2. Параллелограммы ABCD и ADFE лежат в разных плоскостях. Прямая m, параллельная ВС, пересекает плоскости (АВЕ) и (DCF) соответственно в точках Н и Р. Доказать, что HPFE – параллелограмм. | 2. Вне плоскости α расположен Δ АВС, у которого медианы АА1 и ВВ1 параллельны плоскости α. Через вершины В и С проведены параллельные прямые, пересекающие α соответственно в точках E и F. Доказать, что ECBF – параллелограмм. |
3. DABC – тетраэдр,  DBA = = DBA = =  DBC = 90°, DB = 6, АВ = ВС = = 8, АС = 12.
Постройте сечение тетраэдра плоскостью, проходящей через середину DB и параллельной плоскости ADC.
Найти Sсеч. DBC = 90°, DB = 6, АВ = ВС = = 8, АС = 12.
Постройте сечение тетраэдра плоскостью, проходящей через середину DB и параллельной плоскости ADC.
Найти Sсеч.
| 3. Все грани параллелепипеда ABCDA1B1C1D1 – квадраты со стороной а. Через середину AD параллельно плоскости DA1B1 проведена плоскость. Найти Рсеч. |
Дата добавления: 2018-09-20; просмотров: 1463; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
