I. Объяснение нового материала.
Каково может быть взаимное расположение двух прямых на плоскости (совпадают, пересекаются, являются параллельными)? Дайте определение параллельных прямых на плоскости.

Определение параллельных прямых в пространстве – то же.
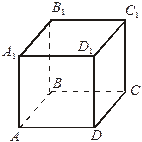
| Дан куб. Все грани – квадраты. Являются ли параллельными прямые АА1 и DD1, АА1 и СС1? Ответ обоснуйте. А прямые АА1 и DC параллельны? Они пересекаются? |
Значит, в пространстве есть прямые, которые не пересекаются, но не являются параллельными, так как не лежат в одной плоскости. Такие прямые называются скрещивающимися (а ¸ b).
Две прямые называются скрещивающимися, если они не лежат в одной плоскости.
По рисунку назовите пары скрещивающихся ребер; пары параллельных ребер.

Итак, алгоритм распознавания взаимного расположения двух прямых в пространстве.

II. Решение задач.
1. Всегда ли две непересекающиеся прямые в пространстве параллельны? (Устно.)
2. Какие две прямые называются параллельными? (Устно.)
3. Дано а || b. Докажите, что все прямые, пересекающие данные, лежат в одной плоскости.
4. Сколько можно провести в пространстве прямых, проходящих через данную точку, параллельных данной прямой? (п. 4).
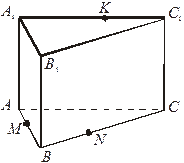
Домашнее задание: теория (п. 4), №№ 16, 89. Постройте сечение многогранника плоскостью (MNK).


Урок 2
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ В ПРОСТРАНСТВЕ.
ПАРАЛЛЕЛЬНОСТЬ ТРЕХ ПРЯМЫХ
Цели : доказать лемму о пересечении плоскости параллельными прямыми, теорему о трех параллельных прямых; показать их применение при решении задач.
Ход урока
I. Проверка домашнего задания (у доски).
II. Устная работа.
1. АВСDА1В1С1D1 – куб. Все грани – квадраты. Установите взаимное расположение прямых.

| AD… А1D1 AD…B1C1 AB1…B1C1 AB1…DC1 B1C1…DC1 BB1…DC |
2. Какие прямые называются параллельными? Скрещивающимися?
III. Объяснение нового материала построить в соответствии с п. 5 учебника.
IV. Решение задач.

| № 17. Дано: DM = MB, DN = NC, AQ = QC, AP = PB, AD = 12, BC = 14. Найдите PMNQP. |
Решение
1. 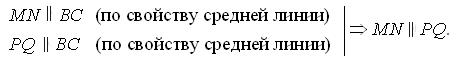
2. 
3. По определению MNQP – параллелограмм.
4. PQ = 7, PM = 6  PMNQP = 2 (7 + 6) = 26.
PMNQP = 2 (7 + 6) = 26.
(Докажите устно, несколькими способами, что MNQP – параллелограмм. Используя признаки параллелограмма.)

| № 19.
Дано: АBCD – параллелограмм,
АВ 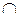 α = K, ВС α = K, ВС 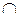 α = F.
Доказать, что AD α = F.
Доказать, что AD 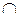 α, DC α, DC 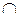 α.
Доказательство
1. α.
Доказательство
1. 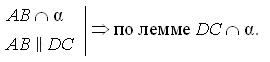 2. Аналогично, AD
2. Аналогично, AD 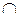 α. α.
|

| № 20.
Дано: ABCD – трапеция, MN – средняя линия, MN 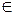 α.
Доказать: пересекают ли ВС и АD плоскость α?
Доказательство
Пусть ВС α.
Доказать: пересекают ли ВС и АD плоскость α?
Доказательство
Пусть ВС 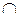 α, тогда α, тогда
|
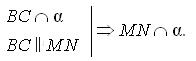
Получили противоречие, так как MN 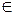 α. Следовательно, ВС
α. Следовательно, ВС 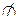 α.
α.
Аналогично АD 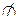 α.
α.

| № 18 (а).
Дано: А 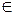 α, СС1 || ВВ1, АС = СВ, ВВ1 = 7.
Найдите СС1. α, СС1 || ВВ1, АС = СВ, ВВ1 = 7.
Найдите СС1.
|
Решение
I. Необходимо доказать, что точки А, С1 и В1 лежат на одной прямой.
1. (А, ВВ1) ≡ β.
2. β 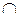 α = АВ1. Докажем, что С1
α = АВ1. Докажем, что С1 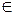 АВ1.
АВ1.
3. Пусть С1 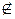 АВ1, тогда СС1
АВ1, тогда СС1 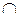 β = С.
β = С.
 Противоречие условию, ВВ1
Противоречие условию, ВВ1 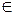 β.
β.
Следовательно, С1 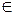 АВ1. (Проведите различные доказательства, проводя плоскость βчерез А и СС1, через СС1и ВВ1).
АВ1. (Проведите различные доказательства, проводя плоскость βчерез А и СС1, через СС1и ВВ1).
II. СС1 – средняя линия DАВВ1 Þ СС1 = 3,5.
Домашнее задание: теория (п. 4 – 5), №№ 18 (б), 21, 88. Построить сечение многогранника плоскостью (MNK).
Урок 3
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ В ПРОСТРАНСТВЕ.
ПАРАЛЛЕЛЬНОСТЬ ТРЕХ ПРЯМЫХ
Цель : закрепить навык применения теорем о параллельных прямых при решении задач.
Ход урока
Дата добавления: 2018-09-20; просмотров: 1208; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
