I. Проверка домашнего задания.

ВВЕДЕНИЕ. Аксиомы стереометрии и их следствие. 5 часов

Урок 1
ПРЕДМЕТ СТЕРЕОМЕТРИИ. АКСИОМЫ СТЕРЕОМЕТРИИ

Цель : рассмотреть основные свойства плоскости.

Ход урока

I. Вступительная беседа.

В планиметрии все фигуры, которые рассматривались при доказательстве каждой теоремы или при решении задач, располагались на плоскости (на листе бумаги или на доске и т. д.). Таким образом, мы имели дело только с одной плоскостью, и все точки, линии, углы, вообще геометрические фигуры лежали только на ней.

В курсе стереометрии нам предстоит рассматривать такие случаи, когда не все точки, линии и углы данной или данных фигур будут располагаться на одной плоскости. Будем считать, например, поверхность стола моделью плоскости Р; возьмем куб и поставим его одной гранью на стол. Легко видеть, что в данном кубе:

1) имеются точки, ребра, углы, лежащие на данной плоскости Р (на столе);

2) имеются точки, которые находятся вне плоскости Р;

3) имеются ребра, пересекающие плоскость Р;

4) имеются углы, находящиеся вне плоскости Р;

5) имеются шесть граней, являющиеся моделями шести различных плоскостей.

Вывод . Плоскости могут вступать во взаимодействие с другими элементами фигур и друг с другом.

Отсюда вытекает необходимость изучать различные случаи комбинаций плоскостей между собой, комбинации плоскостей с линиями и другими геометрическими объектами. Это изучение является одной из задач курса стереометрии. В первую очередь надо выяснить основные свойства плоскостей по отношению друг к другу, к точкам и прямым.

Введем обозначения:

точки – А, В, С и т. д.

прямые – a, b, с и т. д. или (АВ, СD и т. д.)

плоскости – α, β, γ и т. д.

II. Основные свойства плоскости.

Всем знакома ситуация: если ножки стула не одинаковые по длине, то стул стоит на трех ножках, то есть опирается на три «точки», а конец четвертой ножки (четвертая «точка») не лежит в плоскости пола, а висит в воздухе.

Этот пример служит наглядным подтверждением того факта, что через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

Так как три точки, не лежащие на одной прямой, однозначно определяют плоскость, то можно обозначать плоскость как (АВС), (BCD) и т. д.

Можно ли провести плоскость через три точки, лежащие на одной прямой? Сколько существует таких плоскостей?

Верно ли, что:

а) любые три точки лежат в одной плоскости;

б) любые четыре точки лежат в одной плоскости;

в) любые четыре точки не лежат в одной плоскости;

г) через любые три точки проходит плоскость, и притом только одна?

Ответы: а) да; б) нет; в) нет; г) нет.

Рассмотрим следующую ситуацию: для проверки «ровности» при укладке тротуарной плитки используют брусок, который прикладывают к поверхности дорожки. Если на дорожке есть ложбинки или бугорок, то в каких-то местах между бруском и плоскостью дорожки образуется просвет. Если поверхность дорожки ровная, то между бруском и дорожкой никакого просвета нет, то есть брусок всеми своими точками прилегает к ее поверхности.

Можно встретить и обратную ситуацию, когда проверяют «ровность» линейки при помощи проверенной модели плоскости.

Эти примеры служат наглядным подтверждением того факта, что если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

Верно ли, что прямая лежит в плоскости данного треугольника, если она:

а) пересекает две стороны треугольника;

б) проходит через одну из вершин треугольника?

Ответ обоснуйте.

Обратимся к модели куба.

Учащимся прелагается на модели куба указать:

1) точку, принадлежащую одновременно двум данным пересекающимся граням;

2) точку, принадлежащую трем данным пересекающимся граням;

3) грани, которым принадлежит точка, взятая на каком-нибудь ребре куба;

4) грани, которым принадлежит данная вершина куба.

Вывод . Точка, лежащая на линии пересечения двух плоскостей, лежит на каждой из этих плоскостей, и обратно: точка, лежащая одновременно на двух каких-нибудь плоскостях, лежит на линии пересечения этих плоскостей.

На вопрос, что является линией пересечения двух плоскостей (в теоретико-множественном смысле: если прямые имеют хотя бы одну общую точку), отвечает третья аксиома: если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через данную точку.

Наглядной иллюстрацией третьей аксиомы является пересечение двух смежных сторон классной комнаты, пересечение двух листов книги и т. д.

Могут ли две пересекающиеся плоскости иметь общую точку, не принадлежащую линии пересечения этих плоскостей?

Прямые а и b пересекаются в точке С. Через прямую а проходит плоскость α, а через прямую b – плоскость β, отличная от α. Как проходит линия пересечения этих плоскостей?

Следует обязательно отметить, что в пространстве существует бесконечно много плоскостей, и в каждой плоскости справедливы все аксиомы и теоремы планиметрии.

III. Решение задач.

№ 9 (перечертите чертеж и ответы запишите с помощью символики).

Постройте изображение куба АВСDА₁В₁С₁D₁:

а) назовите плоскости, в которых лежат точка М, точка N;

б) найдите точку F – точку пересечения прямых MN и ВС. Каким свойством обладает точка F? (Принадлежит и прямой MN, и плоскости (АВС));

в) найдите точку пересечения прямой KN и плоскости (АВС).

Домашнее задание: теория(п. 1 – 2),№ 1 (перечертите чертеж и ответы запишите с помощью символики), №№ 3, 10, 12, 13.

Урок 2
НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ АКСИОМ

Цель : доказать некоторые следствия из аксиом.

Ход урока

I. Проверка домашнего задания (фронтальная).

II. Устная работа.

Найдите ошибку. Обоснуйте ответ.

MN BD = O AB₁ A₁D = Q

По чертежу назовите: а) линию пересечения плоскостей (АВС) и (АА₁В₁); б) плоскости, которым принадлежат точка М, точка В; в) плоскость, в которой лежит прямая MN; прямая KN.

Постройте:

а) точку пересечения прямой MN и плоскости (АВС);

б) точку пересечения прямой MN и плоскости (А₁В₁С₁);

в) линию пересечения плоскостей (АВС) и (MNK);

г) точку пересечения прямой КN c плоскостью (АВС);

д) линию пересечения плоскостей (АА₁В₁) и (MNK).

Каждый раз при построении аксиомы проговариваются, результат построения записывается с помощью символики.

III. Объяснение нового материала строится согласно п. 3 учебника.

IV. Решение задач.

№№ 4, 5, 7, 9, 11.

Образец оформления.

№ 11.

Дано: а, А а. Доказать, что все прямые, проходящие через точку А и пересекающие прямую, лежат в одной плоскости.

Доказательство

1. Проведем плоскость α = (а, А).

2. Проведем b: А b, b а = В.

3.	Аналогично, любая другая прямая, удовлетворяющая условию задачи, принадлежит плоскости α.

Домашнее задание: теория (п. 3), №№ 6, 8, 14, 15.

Урок 3
РЕШЕНИЕ ЗАДАЧ НА ПРИМЕНЕНИЕ
АКСИОМ СТЕРЕОМЕТРИИ И ИХ СЛЕДСТВИЙ

Цель : сформировать навык применения аксиом стереометрии и их следствий при решении задач.

Ход урока

I. Проверка домашнего задания.

II. Устная работа.

1. Заполните пропуски, чтобы получилось верное утверждение:

а) если A a, a α, то A...α.

б) если A α, B α, то AB...α.

в) если A α, B α, C AB, то C...α.

г) если M α, M β, α β = a, то M...a.

2. По рисунку ответьте на вопросы:

а) каким плоскостям принадлежат точки А, М, K, D, Р? б) каким плоскостям не принадлежат точки М, K, А, Р, D? в) каким плоскостям принадлежат прямые DB, DK, АВ, РС, АС? г) в какой точке пересекаются прямая AD и плоскость (АВС); BD и (ADC); DK и (АВС); АВ и (PDC)?

д) по какой прямой пересекаются плоскости (ABD) и (BDC); (АВС) и (ADC); (АВС) и (ABD); (ABD) и (ADC); (PDC) и (ABC)?

3. Ответьте на вопросы:

а) могут ли прямая и плоскость иметь только одну общую точку? (Да.) Только две общие точки? (Нет.)

б) можно ли провести плоскость через четыре произвольные точки пространства? (Нет.)

в) можно ли через точку пересечения двух прямых провести третью прямую, не лежащую с ними в одной плоскости? (Да.)

III. Решение задач.

1. Начертите изображение тетраэдра АВСD, выберите произвольно точки М АВ, N AD. Постройте линии пересечения плоскостей (ABD) и (CMN); (CMN) и (АВС); (CMN) и (ADC).

2. Начертите изображение куба ABCDA₁B₁C₁D₁, выберите точки M и N грани ABCD. Постройте линии пересечения плоскостей (АВС) и (А₁MN); (В₁MN) и (ВСС₁); (С₁MN) и (СС₁D).

3. Дано: ABCDA₁B₁C₁D₁ – параллелепипед. М А₁В₁. N АА₁. K ВС. Постройте сечение параллелепипеда плоскостью (MNK).

Замечание. В курсе основной школы вы получили представление о многограннике как о геометрическом теле, поверхность которого состоит из многоугольников.

Рассмотрим пересечение некоторого многогранника, например куба, и плоскости α; оно может быть пустым множеством, точкой, отрезком, многоугольником. Если пересечение многогранника и плоскости есть многоугольник, то этот многоугольник называется сечением многогранника данной плоскостью.

Домашнее задание:

1. Дано: ABCA₁B₁C₁ – треугольная призма. М АВ.

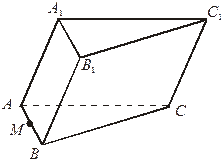
	Постройте: а) точку пересечения прямой А₁М и плоскости (ВВ₁С₁); б) линию пересечения плоскостей (А₁МС₁) и (ВВ₁С₁); в) линию пересечения плоскостей (А₁МС₁) и (АВС); г) сечение призмы плоскостью (А₁МС₁).
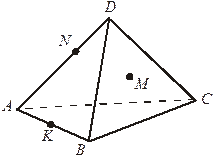
	2. Дано: ABCD – пирамида. М (BDC), N AD, K АВ. Постройте сечение пирамиды плоскостью (MNK).

Урок 4
РЕШЕНИЕ ЗАДАЧ НА ПРИМЕНЕНИЕ
АКСИОМ СТЕРЕОМЕТРИИ И ИХ СЛЕДСТВИЙ

Цель : сформировать навык применения аксиом стереометрии и их следствий.

Ход урока

Дата добавления: 2018-09-20; просмотров: 1483; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!