Проверочный расчет прочности и устойчивости.
2.3.2.1. При оценке прочности переборки контролируются следующие напряжения:
- напряжения в меридиональных и конических сечениях переборки вдали от опорного контура
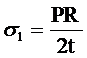 ; (2.31)
; (2.31)
- напряжения в конических сечениях в районе опорного контура
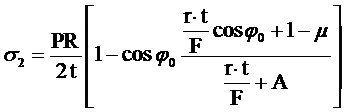 ; (2.32)
; (2.32)
- напряжения в меридиональных сечениях в районе опорного контура
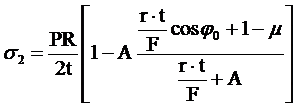 . (2.33)
. (2.33)
В этих выражениях j0 , половина центрального угла сегмента сферической оболочки (см. рис.2.3) и параметр А определяется по формулам
 , (2.34)
, (2.34)
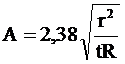 . (2.35)
. (2.35)
Заметим, что сопоставляя напряжения в меридиональных и конических сечениях у опорного контура, можно судить об оптимальности площади распорного кольца (в оптимальном варианте абсолютные величины напряжения s2 и s3 близки).
2.3.2.2. Проверка устойчивости полотнища переборки производится по формуле
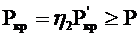 , (2.36)
, (2.36)
где
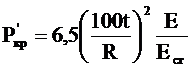 . (2.37)
. (2.37)
Коэффициент  может быть вычислен по выражению (……) в зависимости от s¢кр
может быть вычислен по выражению (……) в зависимости от s¢кр
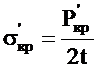 . (2.38)
. (2.38)
Прочная рубка.
Основные положения.
Рубки ГА нагружены внешним гидростатическим давлением, которое изменяется с изменением глубины погружения и должны быть равнопрочные с прочным корпусом. Поэтому в качестве расчетной нагрузки для рубок принимается расчетное давление, принятое при расчете основных элементов ПК.
Размеры рубки должны быть достаточными для размещения в ней необходимых механизмов, устройств и приборов. Форма рубки должна обеспечивать хорошую обтекаемость ограждения рубки, в связи с чем её ширина должна быть минимальной. Наиболее распространены рубки в виде кругового овального (эллиптического) цилиндра. Крыша рубки имеет обычно сферическую форму. Стенки рубки, как правило, подкрепляются ребрами жесткости, предназначенными для восприятия больших изгибающих моментов и повышения устойчивости обшивки.
Круговая рубка.
Круговые рубки являются наиболее часто встречающимся типом рубок, так как имеют простую и экономичную конструкцию.
Конструктивная схема круговой цилиндрической рубки показана на рис 2.4. Круговая рубка представляет собой замкнутую круговую цилиндрическую оболочку, подкрепленную кольцевыми ребрами жесткости. Роль рёбер состоит в обеспечении устойчивости обшивки и восприятии изгибающих моментов, вызванных начальными отклонениями от правильной круговой формы. Сверху рубка жестко соединена с крышей рубки, представляющей собой либо сферическую оболочку, либо сочетание сферической и торовой оболочек. В нижней части рубка прочно соединена с прочным корпусом ГА.
Вследствие симметрии нагрузки и конструкции относительно оси рубки, она по всей своей высоте, за исключением небольшого участка в месте присоединения к прочному корпусу, находится в состоянии осе симметричной деформации. Поэтому определение толщины обшивки, шпации, размеров ребер жесткости рекомендуется производить такие как это делалось для прочного корпуса. Полученные расчетом размеры элементов рубки должны быть откорректированы исходя из конструктивных и других соображений.
Крыша рубки может быть расписана по схеме, приведенной для сферических оболочек.
Эллиптические рубки.
Эллиптическая форма рубки в габаритном отношении более удобна, чем круглая, но она менее выгодна с точки зрения сопротивляемости её давлению воды. Однако эта её сопротивляемость сильно повышается при уменьшении отношения высоты рубки к её поперечным размерам за счет увеличения жесткости стенки благодаря участию жестких торцевых конструкций (крыша рубки и прочный корпус) в восприятии действующей на рубку нагрузки. В этом случае касательные усилия, развивающиеся по линиям примыкания стенок рубки к её торцевым конструкциям, будут увеличивать действующие в её сечениях цепные усилия, предотвращая большой изгиб стенки и создавая оболочке рубки практически безмоментное состояние. Это даст возможность рассчитывать прочность и устойчивость короткой эллиптической оболочки без учета изгиба, т.е. исходя из безмоментности её напряженного состояния. В этом случае можно, делая ошибку в заведомо безопасную сторону, вести указанные расчеты как для цилиндрической оболочки, принимая радиус этой оболочки равным наибольшему радиусу кривизны R эллиптического сечения рубки, определяемому выражением
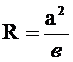 , (2.39)
, (2.39)
где 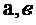 - полудлина и полуширина рубки (большая и малая полуоси эллипса соответственно). Будем считать, что габаритные размеры рубки: длина – 2a, ширина -
- полудлина и полуширина рубки (большая и малая полуоси эллипса соответственно). Будем считать, что габаритные размеры рубки: длина – 2a, ширина - 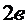 , высота L известны (определены по конструктивным, эксплуатационным, мореходным или другим соображениям).
, высота L известны (определены по конструктивным, эксплуатационным, мореходным или другим соображениям).
Тогда, принимая, что наибольшее сжимаемое напряжение в продольных сечениях не должно превосходить 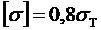 , значение толщины стенки получим по формуле
, значение толщины стенки получим по формуле
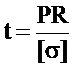 . (2.40)
. (2.40)
Предельную высоту рубки по соображениям устойчивости можно определять из выражения
(2.41)
где коэффициенты 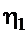 и
и 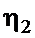 определяются также как для цилиндрической оболочки. Если
определяются также как для цилиндрической оболочки. Если 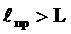 , то стенка рубки должна быть подкреплена шпангоутами.
, то стенка рубки должна быть подкреплена шпангоутами.
Геометрические характеристики поперечного сечения эллиптического шпангоута могут быть подобраны исходя из следующих соотношений:
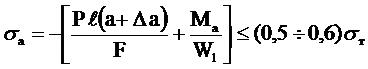 , (2.42)
, (2.42)
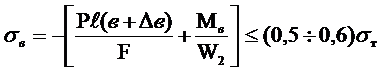 , (2.43)
, (2.43)
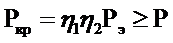 , (2.44)
, (2.44)
где 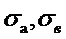 - наибольшее напряжение на концах большой и малой осей эллипса,
- наибольшее напряжение на концах большой и малой осей эллипса,
F - площадь поперечного сечения;
W1, W2 - моменты. сопротивления шпангоута для внутренних и внешних волокон соответственно, определяемые с учетом присоединенного пояска обшивки шириною 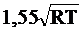 , но не более шпации.
, но не более шпации.
Остальные величины, входящие в зависимости (2.42) - (2,44) находятся по формулам:
- изгибающие моменты на конусах большой и малой осей эллипса
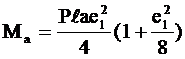 , (2.45)
, (2.45)
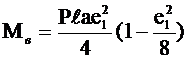 ;
;
- эйлерова нагрузка для шпангоута, рассматриваемого как изолированное кольцо
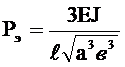 ; (2.46)
; (2.46)
- приращение длин полуосей эллипса
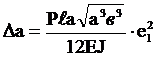 , (2.47)
, (2.47)
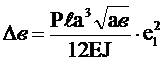 ;
;
- эксцентриситет эллипса с учетом его деформации
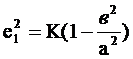 , (2.48)
, (2.48)
где 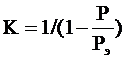 . (2.49)
. (2.49)
Заметим, что при расчете шпангоутных колец, эксцентриситет которых 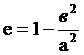 достаточно велик изгибающие момента в кольце оказываются настолько большими, что для их восприятия приходится весьма сильно развивать поперечные сечения шпангоута, вследствие чего величина Pэоказывается настолько большого по сравнению с Р, что можно принимать К=1.
достаточно велик изгибающие момента в кольце оказываются настолько большими, что для их восприятия приходится весьма сильно развивать поперечные сечения шпангоута, вследствие чего величина Pэоказывается настолько большого по сравнению с Р, что можно принимать К=1.
При выполнении проверочного расчета прочности рубки определяются:
- наибольшее нормальное напряжение в поперечных сечениях
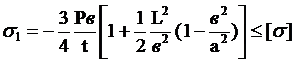 ; (2.50)
; (2.50)
- наибольшее нормальное напряжение в предельных сечениях
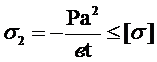 ; (2.51)
; (2.51)
- наибольшее касательные напряжения в стенках рубки
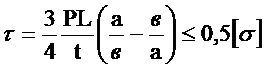 . (2.52)
. (2.52)
Проверка устойчивости обшивки производится по формулам для круговой цилиндрической оболочки, причем для вычисления верхнего критического давления рекомендуется использовать выражение
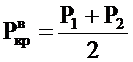 (2.53)
(2.53)
где P1 - верхнее критическое давление, определенное по формуле для цилиндрической оболочке имеющей радиус r=R
P2 - то же для цилиндрической оболочки с радиусом r=a.
Дата добавления: 2018-02-15; просмотров: 38011; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
