I. Объяснение нового материала.

⇐ ПредыдущаяСтр 10 из 19Следующая ⇒

Доказать теорему существования и единственности плоскости, проходящей через любую точку пространства перпендикулярно к данной прямой (п. 17, № 133). Составить обратную теорему, доказать (п. 18).

II. Решение задач.

№№ 123, 132, 135, 137.

III. Домашнее задание: теория (п. 17 – 18), № 134.

Урок 6
ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ

Цель : проверить знание учащимися основных теоретических положений изученной темы.

Ход урока

I. Диктант.

Закончите предложения. Сделайте рисунок.

1. Две прямые называются перпендикулярными, если…

2. Прямая называется перпендикулярной к плоскости, если…

3. Прямая перпендикулярна плоскости, если она…

4. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то…

5. Через данную точку пространства можно провести прямую, ей перпендикулярную, и притом…

6. Все прямые, проходящие через данную точку прямой и перпендикулярные к этой прямой, лежат в…

7. Если одна из двух параллельных прямых перпендикулярна плоскости, то…

8. Две прямые, перпендикулярные одной и той же плоскости,…

9. Если плоскость перпендикулярна одной из двух параллельных прямых, то…

10. Если две плоскости перпендикулярны прямой, то они…

II. Решение задач.

	1. Дано: Е (ABCD). ABCD – прямоугольник. ВЕ АВ, ЕА АD. Доказать, что AD BE. Найти S_EBD, если BD = 7 см, ED = 25 см.
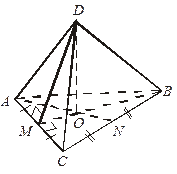
	2. Дано: ABCD – тетраэдр, Δ АВС – правильный, DO (АВС). Доказать, что АВ DC. Доказательство 1. АВ ^ (DMC), так как АВ MD, АВ МС.

	3. Дано: ABCD – тетраэдр, DAC = DAB, АВ = АС. Найдите (AD, ВС).
	4. Дано: ABCDA₁B₁C₁D₁ – параллелепипед. Все грани – равные ромбы. С₁СВ = С₁СD. Найдите (С₁С, ВD), (А₁С, ВD).

Домашнее задание:

1. Через катеты BD и BC прямоугольных треугольников ABD и ABC проведена плоскость α, не содержащая их общий катет. Будет ли АВ α?

2. Отрезок MH пересекает некоторую плоскость в точке K. Через концы отрезка проведены прямые НР и МЕ, перпендикулярные плоскости и пересекающие ее в точках Р и Е. Найдите РЕ, если НР = 4 см, НK = 5 см, МЕ = 12 см.

3. ABCD – квадрат. Отрезок MD перпендикулярен к плоскости АВС. Докажите, что MB АС.

4. ABCD – прямоугольник. Отрезок АЕ перпендикулярен к плоскости АВС. ЕВ = 15, ЕС = 24, ED = 20. Докажите, что треугольник EDC прямоугольный, и найдите АЕ.

5. Точка А принадлежит окружности, АK – перпендикуляр к ее плоскости, АK = 1 см, АВ – диаметр, ВС – хорда окружности, составляющая с АВ угол 45°. Радиус окружности равен 2 см. Докажите, что треугольник KСВ прямоугольный, и найдите KС.

Урок 7
РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ

Цели : ввести понятие расстояния от точки до плоскости; перпендикуляра к плоскости из точки; наклонной, проведенной из точки к плоскости; основания наклонной; проекции наклонной; рассмотреть связь между наклонной, её проекцией и перпендикуляром.

Ход урока

I. Устная работа.

1. Верно ли утверждение: «Прямая перпендикулярна плоскости, если она перпендикулярна двум прямым, лежащим в этой плоскости»?

2. Верно ли утверждение: «Прямая называется перпендикулярной плоскости, если она перпендикулярна некоторой прямой, лежащей в этой плоскости»?

3. Как расположены по отношению друг к другу ребра, выходящие из одной вершины куба?

4. Как расположены плоскости верхней и нижней граней по отношению к боковым ребрам?

5. Что можно сказать о двух (трех, четырех) прямых, перпендикулярных к одной плоскости?

6. Верно ли утверждение: «Две прямые, перпендикулярные третьей прямой, параллельны»?

Дата добавления: 2018-09-20; просмотров: 735; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 5 6 7 8 91011 12 13 14 Следующая ⇒

Мы поможем в написании ваших работ!