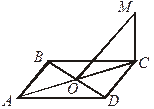
II. Объяснение нового материала.

Как определяется расстояние от точки до прямой на плоскости? (Как кратчайшее расстояние от точки до прямой, как длина перпендикуляра, проведенного из точки к данной прямой.) Вспомнить, как называются отрезки АМ, МН. Определить расстояние от точки до плоскости (п. 19).

III. Решение задач: №№ 138 (а), 139, 140, 143.

№ 143.

Дано: Δ АВС – правильный, АВ = 6 см, М

(АВС), АМ = ВМ = СМ = 4 см. Найдите расстояние от М до (АВС). Решение Опустим перпендикуляр МО к плоскости (АВС). 1. МО

(АВС).

2.Δ АОМ = Δ ВОМ = Δ СОМ (как прямоугольные по гипотенузе и катету) АО = ВО = СО, то есть О – центр описанной около Δ АВС окружности.

3. R = , R = см.

4. Δ МОС – прямоугольный, МО = 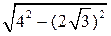= 2 см.

Если точка равноудалена от всех вершин многоугольника, то во что она проецируется на его плоскости?

Составьте обратное утверждение для № 143.

Докажите, что любая точка прямой, перпендикулярной плоскости треугольника и проходящей через центр описанной около него окружности, равноудалена от всех его вершин. (Для доказательства можно использовать тот же рисунок.)

Верно ли утверждение: «Любая точка прямой, проходящей через центр описанной около многоугольника окружности перпендикулярно к плоскости этого многоугольника, равноудалена от всех его вершин» (№ 200).

Далее определяется расстояние между двумя параллельными плоскостями, между плоскостью и параллельной ей прямой (№ 144), между скрещивающимися прямыми (п. 19). Делаются соответствующие рисунки.

Домашнее задание: теория (п. 19), №№ 138 (б), 141, 142.

Урок 8
ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ

Цель : доказать теорему о трех перпендикулярах.

Ход урока

I. Актуализация знаний.

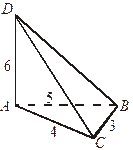
1. Дано: AD

(АВС), АВ = 5, АС = 4, СВ = 3, AD = 6. Определите вид Δ АСВ. Найдите DC и DB. AD – перпендикуляр к плоскости, DC – наклонная, AC – проекция этой наклонной на плоскость (АВС).

По условию задачи проекция АС перпендикулярна прямой СВ, проходящей через основание наклонной – точку С.

Вы доказали, что и наклонная DС перпендикулярна прямой СВ.

Сможем ли мы доказать это утверждение без метрических данных?

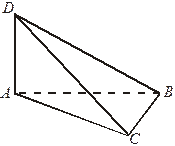
2. Дано: AD (АВС),

АСВ = 90°. Доказать, что: а) AD

CB; б) СВ

(ADC); в) СВ

CD. Какое утверждение вы доказали? Это утверждение получило название теоремы о трех перпендикулярах.

Учитель формулирует теорему о трех перпендикулярах. Доказывает её вместе с учащимися.

Сформулируйте обратную теорему, докажите ее (№ 153).

II. Решение задач: №№ 145, 146, 147.

III. Домашнее задание: теория (п. 20), №№ 148, 149, 150.

№ 150.

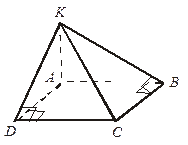
Дано: ABCD – прямоугольник, АK

(АВС), KD = 6 см, KВ = 7 см, KС = 9 см. Найдите ρ(K, (АВС)), ρ (АK, CD).

Решение

1. ρ (K, (АВС)) = АK.

3. Δ KВС – прямоугольный. CB = см.

4. Δ AKD – прямоугольный. AK = 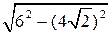= 2 см.

5. ρ(А K, CD) = А D; AD = 4 см.

Урок 9
ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ

Цель : сформировать навык применения теоремы о трех перпендикулярах к решению задач.

Ход урока

I. Проверка домашнего задания (теорема, №№ 149, 150).

II. Устная работа.

	1. Верно ли утверждение: «Если прямая, принадлежащая плоскости, перпендикулярна проекции наклонной на эту плоскость, то она перпендикулярна и самой наклонной»? (Верно.) Обоснуйте ответ.
		2. Верно ли утверждение: «Если прямая перпендикулярна проекции наклонной, то эта прямая перпендикулярна наклонной»? (Неверно.) Какое условие теоремы о трех перпендикулярах здесь не выполняется? (Прямая не принадлежит плоскости.)

3. Установите по рисункам положение прямых а и b.

ABCD – прямоугольник, ABCD – прямоугольник,

BF (АВС) BF (АВС)

ABCD – ромб, ABCD – ромб,

BF (АВС) BF (АВС)

III. Решение задач (по готовым чертежам).

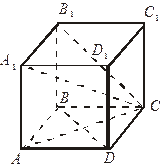
	1. В кубе ABCDA₁B₁C₁D₁: 1) ребро А₁В₁перпендикулярно диагонали В₁С грани ВСС₁В₁; 2) диагональ А₁С перпендикулярна диагонали BD основания ABCD. Докажите.
	2. 1) Дано: А = 30°; АВС = 60°, DB АВС. Докажите, что СD АС.
	2) Дано: ВАС = 40°, АСВ = 50°, AD АВС. Докажите, что СВ BD.
	3. 1) Дано: МА (АВС), АВ = АС, CD = BD. Докажите, что MD ВС 2) Дано: МА (АВС), BD = CD, MD ВС. Докажите, что АВ = АС.
	4. Дано: АЕ и CF – высоты, ВK АВС. Докажите, что KD АС.
	5. Дано: Δ АВС, BD (АВС), АМ = MD, М – центр описанной около Δ АDС окружности. Найдите ACD + ACB.

IV. Решение задач: №№ 154, 156.

Домашнее задание: №№ 155, 159.

Урок 10
ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ

Цель : сформировать навык применения теоремы о трех перпендикулярах к решению задач.

Ход урока

I. Проверка домашнего задания (теорема, №№ 155, 159).

II. Устная работа.

	1. АМ (АВС), АВ = АС, CD = DB. Докажите, что MD ВС.
		2. ABCD – параллелограмм, BM (АВС), МС DC. Определите вид параллелограмма ABCD.
		3. ABCD – параллелограмм, CM (АВС), МO BD. Определите вид параллелограмма ABCD.
		4. Δ АВС, С = 90°, О – центр описанной окружности, АМ = МС, OD (АВС), АВ = 5, АС = 3. Найдите DM.
		5. Δ АВС, АВ = ВС = АС, CD (АВС),АМ = МВ, DM = 15, CD = 12. Найдите S_ADB.
		6. Δ АВС, С = 90°, BD (АВС), AD = 2 BD. Найдите 1 + 2.
		7. ABCD – квадрат, ВЕ (АВС), ЕАВ = 45°, S_ABCD = 4. Найдите S_Δ_AЕС.

III. Решение задач.

1. Если точка равноудалена от всех сторон многоугольника, то она проецируется на его плоскость в центр вписанной окружности.

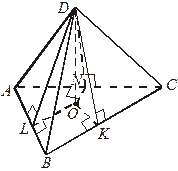
Дано: ML

АВ, MN

АС, МK ВС, МО

(АВС). Доказать, что О – центр вписанной в Δ АВС окружности.

Доказательство

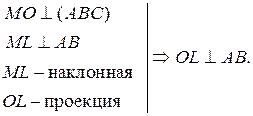
2) Аналогично ОK ВС, ON АС.

3) OL = OK = ON (как проекции равных наклонных).

4) Точка О равноудалена от всех сторон треугольника, следовательно, является центром вписанной в него окружности.

2. Докажите обратное утверждение: «Если через центр вписанной в n-угольник окружности проведена прямая, перпендикулярная плоскости этого n-угольника, то каждая точка этой прямой равноудалена от сторон этого n-угольника». (Для доказательства можно использовать тот же рисунок). №№ 157, 158.

Домашнее задание: №№ 160, 205.

Урок 11
ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ

Цель : сформировать навык решения задач по изученной теме.

Ход урока

I. Проверка домашнего задания (№№ 160, 205).

II. Решение задач (по готовым чертежам).

	1. Δ АВС, D 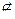(АВC), AD = BD = СD, АОВ = 60°. Найдите АСВ.
	2. Δ АВС, АВ = ВС = АС, О – центр Δ АВС, DO (АВС), DC = 10, DO = 8. Найдите S_АВС, расстояние от точки D до сторон Δ АВС.
	3. Δ АВС, АВ = ВС = АС, О – центр Δ АВС, DO (АВС), DМ = 5, DO = 4. Найдите Р_Δ_АВС, AD, BD, DC.
	4. Δ АВС, АСВ = 90°, АО = ОВ, DO (АВС), DC = 5, DO = 3. Найдите R описанной около Δ АВС окружности, АВ, AD, DB.
	5. Δ АВС, АС = СВ = 10, АВ = 12, DM АВ, DN АС, DK ВС, DM = DN = DK, DO (АВС), DO = 1. Найдите DC.

III. Решение задач: №№ 199, 202, 203, 207.

Домашнее задание: №№ 204, 206.

Урок 12
УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ

Цели : ввести понятие прямоугольной проекции фигуры; дать определение угла между прямой и плоскостью.

Ход урока

I. Объяснение нового материала построить в соответствии с п. 21.

II. Решение задач: №№ 151, 163, 208, 209.

III. Решение задач (по готовым чертежам).

	1. ABCD – квадрат, S_ABCD= 4, CM α, CM = 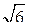. Найдите угол между прямой АС и плоскостью α.
	2. ABCDA₁B₁C₁D₁– куб. Найдите угол между прямой DB₁ и плоскостью (DD₁C₁).
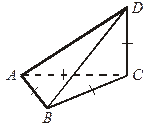
	3. Δ АВС, АВ = ВС = АС, CD (АВС),DC = АС. Найдите синус угла между прямой BD и плоскостью ADC.

Домашнее задание: теория (п. 21), №№ 164, 165.

Урок 13
ЛАБОРАТОРНО-ПРАКТИЧЕСКАЯ РАБОТА

Цели : сформировать конструктивный навык нахождения угла между прямой и плоскостью; расстояния от точки до прямой; научить обосновывать или опровергать выдвигаемые предположения.

Ход урока

Учащимся выдаются готовые бланки, на которых они выполняют задания. Лабораторно-практическая работа построена на основе варьирования условий. «Одинаковые» картинки и разные к ним условия должны заставить учащихся думать, обосновывать или опровергать свои гипотезы, научить применять изученные теоретические положения.

Учитель должен требовать от учащихся проговаривания всех определений и теорем.

Дата добавления: 2018-09-20; просмотров: 1584; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 6 7 8 9 101112 13 14 15 Следующая ⇒

Мы поможем в написании ваших работ!