III. Объяснение нового материала.

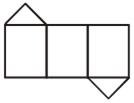
Виды призм

Устно № 218.

Далее ввести понятие боковой поверхности, полной поверхности прямой призмы (п. 30). Можно использовать развертки призм.

IV. Решение задач: №№ 221, 222, 225, 230.

Домашнее задание: теория (п. 30), №№ 224, 229, 231.

Урок 3
ПРИЗМА. НАКЛОННАЯ ПРИЗМА

Цель : вывести формулу для вычисления боковой поверхности наклонной призмы, сформировать навык ее использования при решении задач.

Ход урока

I. Проверка домашнего задания.

II. Устная работа.

Продолжите предложения.

1) Призма называется наклонной, если…

2) Призма является прямой, если…

3) Призма называется правильной, если…

4) Боковой поверхностью призмы называется…

5) Площадью полной поверхности призмы называется сумма…

6) Площадь боковой поверхности прямой призмы равна произведению…

7) Все двугранные углы при боковых гранях прямой призмы…

8) Правильная четырехугольная призма, высота которой равна стороне основания, является…

Ответьте на вопросы.

1) В какой призме боковые ребра параллельны ее высоте?

2) Если все ребра призмы равны, то будет ли она правильной? Ответ поясните.

3) Существует ли призма, у которой только одна боковая грань перпендикулярна основанию? Ответ поясните.

4) Может ли диагональ прямоугольного параллелепипеда быть меньше:

а) бокового ребра?

б) стороны основания?

в) диагонали боковой грани?

5) Дан наклонный параллелепипед. Известно, что угол основания равен 150°. Какое из диагональных сечений параллелепипеда больше?

6) Будет ли сечение, перпендикулярное боковому ребру призмы, перпендикулярно к ее боковой грани? Ответ обоснуйте.

Выберите верный ответ из числа предложенных.

1) Чему равна площадь боковой поверхности куба с ребром 10 см?

а) 40 см²; б) 400 см²; в) 100 см²; г) 400 см.

2) Чему равна площадь полной поверхности куба с ребром 6 см?

а) 36 см²; б) 144 см²; в) 216 см²; г) 144 см.

3) Чему равна площадь боковой поверхности правильной четырехугольной призмы, если её высота h, сторона основания а?

а) ha; б) 4ah; в) 4²h; г) 4(a + h).

4) Чему равна площадь полной поверхности куба, если его диагональ равна d ?

а) 2d ²; б) 6d ²; в) 3d ²; г) 4d ²^..

5) Прямоугольный параллелепипед имеет три измерения, равные а = 5 см; b = 8 см; h = 10 см. Какова площадь его полной поверхности?

а) 400 см²; б) 160 см²; в) 280 см²; г) 340 см².

6) По стороне основания а и боковому ребру b найдите полную поверхность правильной треугольной призмы.

а) ; б) + 3ab; в) a² + 3ab; г) 3a ( + 2).

III. Решение задач: №№ 227, 228, 236, 237.

Домашнее задание: теория (п. 30), №№ 238, 295, 297.

Дополнительно (см.: Зив Б. Г., Мейлер В. М., Баханский А. Г. Задачи по геометрии. – М.: Просвещение, 1997.).

1) В наклонной треугольной призме ABCA₁B₁C₁ основанием служит прямоугольный треугольник АВС ( С = 90°). Плоскость боковой грани АА₁С₁С перпендикулярна плоскости основания. Докажите, что СС₁В₁В – прямоугольник.

2) В наклонной треугольной призме угол между двумя боковыми гранями прямой. Площади этих граней равны 50 и 120 см². Длина бокового ребра 10 см. Найдите площадь боковой поверхности призмы.

1) Основанием наклонного параллелепипеда ABCDA₁B₁C₁D₁ служит прямоугольник ABCD. Плоскости граней AA₁D₁D и ВВ₁С₁С перпендикулярны плоскости основания. Докажите, что остальные боковые грани – прямоугольники.

2) В наклонной треугольной призме АВСА₁В₁С₁ угол между гранями АА₁С₁С и СС₁В₁В прямой. Найдите площадь боковой поверхности призмы, если боковое ребро равно 5 см, а площади граней АА₁В₁В и СС₁В₁В равны соответственно 130 и 50 см².

1) Основанием наклонной треугольной призмы ABCA₁B₁C₁ служит равнобедренный треугольник АВС, АВ = АС, А₁АС = А₁АВ < 90°. Докажите, что СС₁В₁В – прямоугольник.

2) В наклонной треугольной призме площади двух боковых граней равны 40 и 80 см². Угол между ними равен 120°. Найдите площадь боковой поверхности призмы, если длина бокового ребра равна 10 см.

1) Основанием наклонной треугольной призмы ABCA₁B₁C₁ служит правильный треугольник АВС. Вершина А₁ равноудалена от всех вершин нижнего основания. Докажите, что СС₁В₁В – прямоугольник.

2) В наклонной треугольной призме площади двух боковых граней равны 6 и 3 см². Угол между ними равен 135°. Найдите площадь боковой поверхности призмы, если длина бокового ребра равна 3 см.

Урок 4
ПРИЗМА

Цель : сформировать навык решения задач по изученной теме.

Ход урока

Решение задач: №№ 232, 233, 234, 235.

Домашнее задание: №№ 290, 296, 298.

Урок 5
ПИРАМИДА

Цель : ввести понятие пирамиды, площади полной поверхности пирамиды.

Ход урока

I. Объяснение нового материала построить в соответствии с пунктом 28.

Контрольные вопросы.

1. Среди изображенных тел выберите номера тех, которые являются пирамидами.

1 2 3 4 5

6 7 8 9

2. Назовите:

а) основание пирамиды; б) высоту; в) апофему; г) диагональное сечение; д) сколько их проведено, сколько можно еще провести; е) какая это пирамида?

3. Продолжите предложения.

1) Высотой пирамиды называется…

2) Апофемой пирамиды называется…

3) Площадью полной поверхности пирамиды называется…

4) Площадью боковой поверхности пирамиды называется…

5) Диагональное сечение пирамиды – сечение пирамиды плоскостью, проходящей через два несоседних…

II. Решение задач: №№ 240, 241, 242, 245.

Домашнее задание: теория (п. 32), №№ 239, 243, 244.

Урок 6
ПИРАМИДА. ПРАВИЛЬНАЯ ПИРАМИДА

Цель : ввести понятие правильной пирамиды.

Ход урока

I. Проверка домашнего задания (№№ 243, 244).

II. Устная работа.

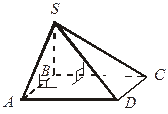
1. Дано: SBA

ABCD, SBC

ABCD. ABCD – прямоугольник. Доказать: 1) SB

ABCD; 2)

SAB – линейный угол SADC.

2. Основание пирамиды – прямоугольник, одно боковое ребро перпендикулярно основанию пирамиды. Определить вид боковых граней.

	3. Дано: SABCD – пирамида, ABCD – квадрат, АВ = 2, SAB = 60°. Найдите S_бок.
	4. Дано: SABCD – пирамида, ABCD – ромб, АВ = BD, Р_ABCD = 16, SO (АВС), SO = 1. Найдите S_бок.
	5. Дано: SABCD – пирамида, ABCD – ромб, АС = 6, BD = 8, SO (АВС), SO = 1. Найдите S_бок.

III. Объяснение нового материала (п. 29)

IV. Решение задач: №№ 254, 255, 257.

Домашнее задание: теория (п. 33), №№ 256, 258, 259.

Контрольные вопросы

Продолжите предложения.

1. У правильной пирамиды:

а) боковые ребра…

б) боковые грани…

в) апофемы…

г) двугранные углы при основании…

д) двугранные углы при боковых ребрах…

2. Каждая точка высоты правильной пирамиды равноудалена от всех _________________ основания.

3. Каждая точка высоты правильной пирамиды равноудалена от всех _________________ граней.

4. Боковыми гранями правильной пирамиды являются…

5. Площадь боковой поверхности правильной пирамиды равна произведению полупериметра основания на…

Урок 7
ПИРАМИДА. ПРАВИЛЬНАЯ ПИРАМИДА

Цель : сформировать навык решения задач по изученной теме.

Ход урока

Дата добавления: 2018-09-20; просмотров: 2449; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 10 11 12 13 141516 17 18 19 Следующая ⇒

Мы поможем в написании ваших работ!