I. Проверка домашнего задания.
II. Устная работа.
1. Как в правильной пирамиде найти точку, равноудаленную от всех вершин?
2. Как в правильной пирамиде найти точку, равноудаленную от всех ее граней?

| 3. Дано: SABC – правильная пирамида, SO – высота, АО  ВС, АН ВС, АН  SK, АН SK, АН  SK = Н.
Доказать: AS SK = Н.
Доказать: AS  ВС; АН ВС; АН  CSB. CSB.
|

| 4. Дано: SABC – правильная пирамида, SO – высота, KD  AS.
Доказать: CBD AS.
Доказать: CBD  AS. AS.
|

| 5. Дано: SABC – правильная пирамида, KL || AC, LM || BS.
Доказать: KL  LM. LM.
|

| 6. Дано: SABCD – правильная пирамида, KN || BA, KL || BS. Доказать: KLMN|| ASB, KLMN – трапеция. |

| 7. Дано: SABC – правильная пирамида, KN || BC, NM || AS. Доказать: сечение KLMN – прямоугольник. |
III. Решение задач: №№ 261, 262, 264, 266.
Домашнее задание: теория (п. 29), №№ 260, 263, 265.
Контрольные вопросы
Выберите верный ответ из числа предложенных.
1. Чему равна высота правильной треугольной пирамиды со стороной основания а и боковым ребром b?
а) h =  ; б) h =
; б) h =  ; в) h =
; в) h =  .
.
2. Чему равна сторона основания правильной шестиугольной пирамиды, если её высота h и боковое ребро b?
а) a =  ; б) a =
; б) a =  ; в) a =
; в) a =  .
.
3. Чему равна высота правильной шестиугольной пирамиды со стороной основания а и боковым ребром b?
а) h =  ; б) h =
; б) h = 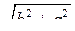 ; в) h =
; в) h =  .
.
4. Чему равна апофема правильной четырехугольной пирамиды со стороной основания а и высотой h?
а) l = 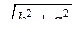 ; б) l =
; б) l =  ; в) l =
; в) l =  .
.
5. Чему равна апофема правильной треугольной пирамиды со стороной а и боковым ребром b?
а) l =  ; б) l =
; б) l =  ; в) l =
; в) l =  .
.
6. Чему равна апофема правильной шестиугольной пирамиды со стороной а и высотой h?
|
|
|
а) l =  ; б) l =
; б) l = 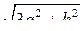 ; в) l =
; в) l = 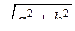 .
.
7. Чему равна площадь полной поверхности правильной пирамиды?
а) S = Ph + Sосн; б) S =  + Sосн; в) S = Pl + Sосн, где h – высота пирамиды, l – апофема, P – периметр основания.
+ Sосн; в) S = Pl + Sосн, где h – высота пирамиды, l – апофема, P – периметр основания.
8. Имеет ли правильная четырехугольная пирамида ось симметрии?
а) да; б) нет.
9. Сколько плоскостей симметрии имеет:
– правильная четырехугольная пирамида?
а) 2; б) 3; в) 4.
– правильный тетраэдр?
а) 1; б) 3; в) не имеет.
10. Дана правильная треугольная пирамида. Верно ли, что ее апофемы равны?
а) да; б) нет.
Урок 8
ПИРАМИДА. КЛЮЧЕВЫЕ ЗАДАЧИ
Цель : рассмотреть свойства пирамид, имеющих равные боковые ребра; равные апофемы.
Ход урока
I. Объяснение нового материала.
1. Вершина пирамиды проецируется в центр описанной около основания окружности, если:
а) боковые ребра пирамиды равны;
б) боковые ребра составляют с плоскостью основания равные углы;
в) боковые ребра составляют с высотой пирамиды равные углы.
Доказать. Составить обратные задачи. Доказать.
2. Вершина пирамиды проецируется в центр вписанной в основание окружности, если:
а) апофемы равны;
б) двугранные углы при ребрах основания равны;
в) апофемы составляют с высотой пирамиды равные углы.
Доказать. Составить обратные задачи. Доказать.
|
|
|
II. Решение задач: №№ 246, 248, 250, 251.
Домашнее задание: теория (знать ключевые задачи), №№ 247, 249, 252.
Контрольные вопросы
1. Боковые ребра пирамиды равны между собой. Может ли основание пирамиды быть: 1) ромбом; 2) прямоугольником; 3) правильным шестиугольником?
2. Боковые ребра пирамиды равны между собой. Как расположена проекция вершины пирамиды на основании, если основание: 1) прямоугольник; 2) прямоугольный треугольник?
3. Двугранные углы при основании пирамиды равны между собой. Может ли в основании пирамиды быть: 1) равнобедренный треугольник; 2) ромб; 3) прямоугольник?
4. Вершина пирамиды проектируется в точку пересечения диагоналей основания. Что можно сказать о двугранных углах при основании пирамиды, если основание: 1) параллелограмм; 2) ромб; 3) равнобедренная трапеция?
Урок 9
УСЕЧЕННАЯ ПИРАМИДА
Цель : ввести понятие усеченной пирамиды.
Ход урока
I. Проверка домашнего задания (№ 252).
II. Устная работа.
| | 1. Дано: SABCD – пирамида, ABCD – параллелограмм, SA = SB = SC = SD.
Найдите  DAB. DAB.
| |||||
| | 2. Дано: ABCD – пирамида, AD = Найдите | |||||

| 3. Дано: SABCD – пирамида, ABCD – трапеция, SO Найдите PABCD. | |||||
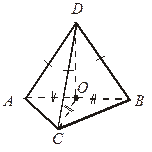
| 4. Дано: ABCD – пирамида,
Определите вид Δ АВС. | |||||
| | 5. Дано: ABCD – пирамида, Найдите DO. | |||||
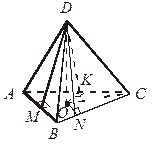
| 6. Дано: ABCD – пирамида, Найдите DO. | |||||
III. Объяснение нового материала построить в соответствии с пунктом 34 учебника.
Обязательно решить в классе задачу № 267. Дополнительно доказать, что сечение – многоугольник, подобный основанию, и площади сечения и основания относятся как квадраты их расстояний от вершины.
№ 267.
Если пирамида пересечена плоскостью, параллельной основанию, то:
1) боковые ребра и высота пирамиды делятся этой плоскостью на пропорциональные части;
2) сечение – многоугольник, подобный основанию;
Дата добавления: 2018-09-20; просмотров: 2847; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!


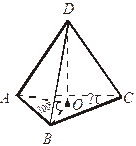
 АВ, АО = ОВ,
АВ, АО = ОВ,