Площади сечения и основания относятся как квадраты их расстояний от вершины.
| Дано: в пирамиде SABCDЕ SO  ABCDE.
A1B1С1D1E1 || ABCDE.
Доказать: 1)  ;
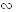2) A1B1С1D1E1  ABCDE;
3)  .
|
Доказательство
1) A1B1С1D1E1 || ABCDE, поэтому A1B1 || АВ, B1С1 || BC, С1D1 || СD, ..., А1О1 || АО (§ 34, теорема 2).
Следовательно, 
; 
; …; 
.
В каждой из этих пропорций имеются попарно одинаковые отношения, и потому .
2) Δ А1SB1 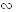Δ ASB, Δ B1SC1 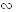Δ BSC, следовательно, 
, 
, откуда .
Аналогично получим:
и 
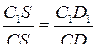, откуда 
и т. д.
Продолжая брать пары подобных треугольников, получим:
...,
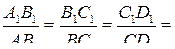то есть стороны сечения пропорциональны сторонам основания. Кроме того, стороны одноименных углов взаимно параллельны, и потому эти углы соответственно равны; следовательно, по определению подобных многоугольников A1B1С1D1E1 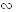ABCDE.
3) A1B1С1D1E1 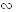ABCDE, следовательно, 
.
Но Δ А1SО1 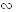Δ ASО и Δ А1SВ1 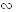Δ АSВ, поэтому 
и 
, откуда 
.
Из (1) и (2) следует, что 
.
Следствие. Площадь сечения, параллельного основанию пирамиды, – квадратная функция расстояния его плоскости от вершины (или основания) пирамиды.
Пусть SO = h, SO1 = х, тогда 
и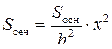 
;
Sосн и h для данной пирамиды величины постоянные, обозначим 
, тогда Sсеч = kx2, то есть площадь сечения – квадратная функция от х, где х – расстояние плоскости сечения от вершины пирамиды.
Задача . В пирамиде сечение, параллельное основанию, делит высоту в отношении 2 : 3 (от вершины к основанию). Найти площадь сечения, зная, что оно меньше площади основания на 84 см2.
| Дано: А1В1С1 || АВС, 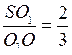 , Sосн – Sсеч = 84 см2.
Найти Sсеч.
Решение
1) (№ 267);
|
2) Sсеч = х; Sосн = х + 84, тогда из 1) 
; 
; 
; 25x = 4 (x + 84); 21x = 4 ∙ 84; x = 4 ∙ 4 = 16.
|
|
|
Ответ: Sсеч = 16 см2.
IV. Решение задач: № 268.
Домашнее задание: теория (п. 34), №№ 269, 270.
Урок 10
УСЕЧЕННАЯ ПИРАМИДА
Цель : сформировать навык решения задач на усеченную пирамиду.
Ход урока
I. Проверка домашнего задания (№№ 269, 270).
II. Устная работа.
1. Сравните изображения многогранников. Выделите признаки, характерные для усеченной пирамиды. Какой из этих многогранников не является усеченной пирамидой?
Как проверить, изображена ли усеченная пирамида?
Какие из следующих многогранников являются усеченными пирамидами?
призматоида
2. Как построить усеченную пирамиду?
3. В пирамиде проведено сечение параллельно основанию через середину высоты. Площадь основания равна Q. Найдите площадь сечения.
4. В тетраэдре через середины трех ребер проведено сечение плоскостью. Что можно сказать о расстоянии вершин тетраэдра до плоскости сечения?
5. Продолжите предложения:
а) основания усеченной пирамиды – …;
б) перпендикуляр, проведенный из любой точки одного основания усеченной пирамиды на плоскость другого, называется…;
в) в усеченной пирамиде боковые грани – …;
г) боковые грани правильной усеченной пирамиды…;
|
|
|
д) высота боковой грани усеченной пирамиды называется…
III. Решение задач.
1. В пирамиде сечение, параллельное основанию, делит высоту в отношении 3 : 4 (от вершины к основанию), а площадь сечения меньше площади основания на 200 см2. Найти площадь основания.
2. На каком расстоянии от вершины пирамиды с высотой h надо провести сечение параллельно основанию, чтобы площадь сечения равнялась: 1) половине площади основания; 2) 
; 3) 
площади основания.
3. Высота правильной четырехугольной усеченной пирамиды равна 7 см, стороны оснований 10 см и 2 см. Найти боковое ребро пирамиды и диагональ.
4. Стороны оснований правильной треугольной усеченной пирамиды 4 дм и 1 дм, боковое ребро 2 дм. Найти высоту и апофему пирамиды.
5. Найти высоту правильных усеченных пирамид: 1) треугольной; 2) четырехугольной; 3) шестиугольной. Даны стороны а и b нижнего и верхнего оснований и угол α наклона бокового ребра к большему основанию.
6. 1) В правильной усеченной четырехугольной пирамиде стороны оснований равны а и b (а > b), двугранный угол при большем основании α. Найти высоту пирамиды. 2) То же, если пирамида треугольная.
7. 1) Высота правильной четырехугольной усеченной пирамиды равна 4 см, стороны оснований 2 см и 8 см. Найти площадь диагонального сечения. 2) Высота правильной четырехугольной усеченной пирамиды равна 4 см, диагональ 5 см. Найти площадь диагонального сечения.
|
|
|
8. В правильной усеченной треугольной пирамиде сторона большего основания а, сторона меньшего b, боковое ребро образует с основанием острый угол α.1) Провести сечение через боковое ребро и центр нижнего основания; 2) найти его площадь.
9. В правильной четырехугольной усеченной пирамиде стороны основания равны 3 см и 5 см, высота 3 см. Провести сечение через противолежащие стороны оснований. Найти: 1) площадь сечения; 2) двугранный угол между сечением и нижним основанием.
Домашнее задание: теория (п. 34), №№ 313, 314.
Урок 11
СИММЕТРИЯ В ПРОСТРАНСТВЕ. ПОНЯТИЕ
ПРАВИЛЬНОГО МНОГОГРАННИКА. ЭЛЕМЕНТЫ
СИММЕТРИИ ПРАВИЛЬНЫХ МНОГОГРАННИКОВ
Цель : ввести понятие правильного многогранника.
Ход урока
Дата добавления: 2018-09-20; просмотров: 1595; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!