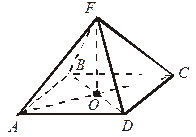
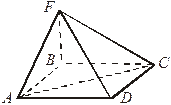
I. Расстояние от точки до прямой
1. AF  (АВС)
(АВС)
Найти расстояние от F до CВ.

| 
| 
|
Δ АВС прямоугольный (  С = 90°) С = 90°)
| Δ АВС равнобедренный | Δ АВС тупоугольный (  С > 90°) С > 90°)
|
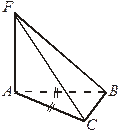
2. Найти расстояние от F до АС.

FB  (АВС) FB
(АВС) FB  (АВС)
(АВС)
ABCD – прямоугольник ABCD – ромб
II. Угол между прямой и плоскостью
1. Найдите угол между B1D и (АВС); между B1D и (DD1C1).
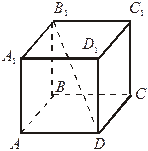

ABCD – прямоугольник ABCD – параллелограмм
АА1  (АВС) АА1
(АВС) АА1  (АВС)
(АВС)
2. ВВ1  (АВС). Найдите угол между ВС1 и (АА1В1).
(АВС). Найдите угол между ВС1 и (АА1В1).
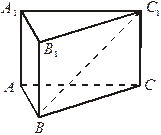

Δ АВС – равносторонний Δ АВС – прямоугольный
(  В = 90°)
В = 90°)
Δ АВС – тупоугольный (  В > 90°)
В > 90°)
| 3. АА1  (АВС).
Найдите угол:
между В1F и (АВС);
между В1F и KK1F1;
между В1F и (АА1В1). (АВС).
Найдите угол:
между В1F и (АВС);
между В1F и KK1F1;
между В1F и (АА1В1).
|
4. BD  (АВС).
(АВС).
Найти угол между CD и плоскостью (АВD).
| 
| 
|
Δ АВС прямоугольный (  С = 90°) С = 90°)
| Δ АВС равносторонний | Δ АВС прямоугольный (  А = 90°) А = 90°)
|
Урок 14
ДВУГРАННЫЙ УГОЛ
Цель : ввести определение двугранного угла.
Ход урока
I. Объяснение нового материала.
Пункт 22 можно прочитать вместе с учащимися.
Один из механизмов построения линейного угла двугранного угла приведен в задаче № 166.
Покажите использование данного механизма.
ABCD – квадрат, FO  (АВС).
(АВС).
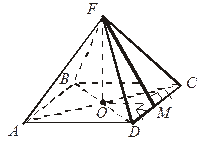
| Постройте линейный угол двугранного угла ADCF.
1. (ADC)  (DFC) = DC.
2. Из точки F к плоскости (ADC) перпендикуляр уже построен. Проведем из точки F перпендикуляр к прямой DC в плоскости (DCF). (DFC) = DC.
2. Из точки F к плоскости (ADC) перпендикуляр уже построен. Проведем из точки F перпендикуляр к прямой DC в плоскости (DCF).
|
Δ DFC – равнобедренный  FM – медиана и высота.
FM – медиана и высота.
|
|
|
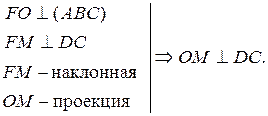
3. 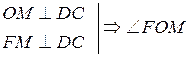 – линейный угол угла ADCF.
– линейный угол угла ADCF.
II. Провести аналогичные рассуждения и выполнить построения.
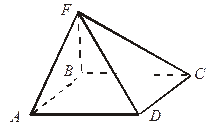
| 1. ABCD – прямоугольник, BF  (АВС).
Найдите (АВС).
Найдите  ((АВС), (FDC)). ((АВС), (FDC)).
|
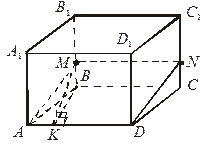
| 2. ABCD – параллелограмм, АА1  (АВС).
Найдите (АВС).
Найдите  CDAM. CDAM.
|
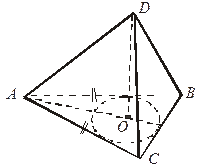
| 3. Δ АВС, АС = АВ, О – центр вписанной окружности.
Найдите  ((АВС), (BCD)), ((АВС), (BCD)),  ((АВС), (ACD)). ((АВС), (ACD)).
|
III. Решение задач: №№ 170, 171.
Домашнее задание: теория (п. 22), №№ 167, 168, 169, 172.
Урок 15
ДВУГРАННЫЙ УГОЛ
Цели : сформировать конструктивный навык нахождения угла между плоскостями; отработать определение двугранного угла.
Ход урока
1. FO  (АВС) FO
(АВС) FO  (АВС)
(АВС)
ABCD – квадрат ABCD – ромб
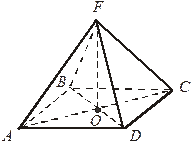

Найдите угол между (АВС) и (FDC);
Найдите угол между (FDC) и (FBC).
2. FB  (АВС) FB
(АВС) FB  (АВС)
(АВС)
ABCD – прямоугольник ABCD – ромб


Найдите угол между (АВС) и (FDC);
Найдите угол между (AFB) и (FBC);
Найдите угол между (AFD) и (FBC).
|
|
|
3. AF 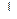 (АВС)
(АВС)

| 
| 
|
Δ АВС прямоугольный ( 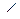 С = 90°) С = 90°)
| Δ АВС равнобедренный | Δ АВС тупоугольный ( 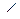 С > 90°) С > 90°)
|
Найти угол между (АВС) и (FCВ).
4. ABCDEF – правильный шестиугольник SB 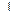 (АВС).
(АВС).
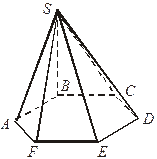
| Найдите угол между: (ABS) и (СBS); (SFE) и (ABC); (ASF) и (ABC); (FSE) и (DSE); (FSE) и (BCS). |
Урок 16
ДВУГРАННЫЙ УГОЛ
Цель : сформировать навык решения задач по данной теме.
Ход урока
Решение задач: №№ 173, 176, 212, 213 (решите эту задачу, используя результат задачи № 212: SАВС = Sпр ∙ cos α), 214 (решите двумя способами).
Домашнее задание: №№ 174, 175, 216.
Урок 17
СВОЙСТВО ДВУГРАННОГО УГЛА
Цель : доказать одно из свойств двугранного угла, часто применяющееся при решении задач.
Ход урока
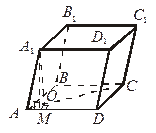
Если два плоских угла трехгранного угла равны, то их общее ребро проецируется на биссектрису третьего плоского угла.
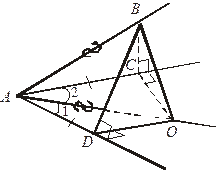
| Дано:  АВС = АВС =  АВD, ВО АВD, ВО 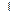 (АDС).
Доказать, что АО – биссектриса (АDС).
Доказать, что АО – биссектриса 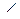 САD.
Доказательство
1. Δ ABD = Δ АВС (как прямоугольные по гипотенузе и острому углу) САD.
Доказательство
1. Δ ABD = Δ АВС (как прямоугольные по гипотенузе и острому углу)   AD = АС. AD = АС.
|
2. Δ ADO = Δ АСО (как прямоугольные по гипотенузе и катету) 

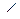 1 =
1 = 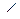 2
2  АО – биссектриса.
АО – биссектриса.
I. Решение задач.
№ 1. Все грани параллелепипеда – равные ромбы, со стороной а и острым углом α. Найдите высоту параллелепипеда.
|
|
|
Решение
| 1. 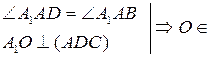 биссектрисе биссектрисе 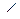 А.
2. А.
2. 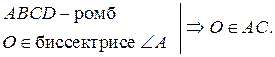
|
3. Проведем ОМ 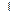 AD.
AD.
По теореме о трех перпендикулярах А1М 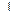 AD.
AD.
4. Δ АА1М – прямоугольный. AM = a ∙ cos α.
5. Δ АОМ – прямоугольный. АО = 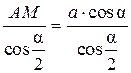 .
.
6. Δ А1АО – прямоугольный.
H = А1О = 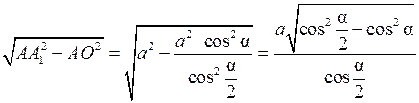 .
.
№ 2. Основанием параллелепипеда является прямоугольник со сторонами а и b. Боковое ребро длины с образует со смежными сторонами основания углы, равные φ. Найдите высоту параллелепипеда.
Решение
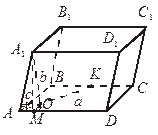
| 1.  биссектрисе биссектрисе 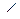 А.
2. А.
2. 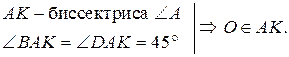
|
3. Проведем ОМ 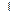 AD. По теореме о трех перпендикулярах А1М
AD. По теореме о трех перпендикулярах А1М 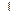 AD.
AD.
4. Δ А1АМ – прямоугольный. AM = c ∙ cos φ.
5. Δ АОМ – прямоугольный. АО = 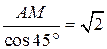 ∙ c ∙ cos φ.
∙ c ∙ cos φ.
6. Δ А1АО – прямоугольный.
H = А1О = 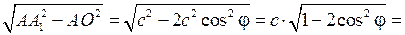
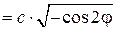 .
.
№ 3. Все грани тетраэдра АBCD – равные равнобедренные треугольники с боковыми сторонами, равными а, и углом между ними – 2α.
Найдите высоту тетраэдра.
Решение
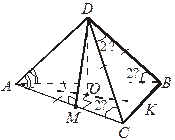
| 1.  биссектрисе биссектрисе 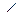 А.
2. А.
2.  AK – медиана и высота. О AK – медиана и высота. О  АK. АK.
|
3. Δ MDC – прямоугольный. DM = a ∙ sin 2α. MC = a ∙ cos 2α.
4. AM = AC – MC = a – a ∙ cos 2α = a (1 – cos 2α) = 2a sin2α.
5. Δ AOM – прямоугольный. OM = AM ∙ tg α = 2a sin2α ∙ tg α.
6. H = DO = 
=  .
.
Домашняя контрольная работа
Вариант I
1. Чему равен угол между ребром двугранного угла и любой прямой, лежащей в плоскости его линейного угла?
|
|
|
2. Треугольник АВС – прямоугольный ( 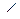 С = 90°),
С = 90°), 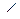 А = 30°, АС = а, DC
А = 30°, АС = а, DC 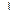 АВС. DC =
АВС. DC = 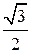 a. Чему равен угол между плоскостями ADB и ACB?
a. Чему равен угол между плоскостями ADB и ACB?
3. Через вершину прямого угла С равнобедренного прямоугольного треугольника АВС проведена плоскость α, параллельная гипотенузе и составляющая с катетом угол 30°. Найдите угол между плоскостью АВС и плоскостью α.
Вариант II
1. Плоскость α пересекает грани двугранного угла по прямым АВ и АС. Две пересекающиеся прямые, лежащие в плоскости α, перпендикулярны к ребру этого угла. Докажите, что  ВАС – линейный угол этого двугранного угла.
ВАС – линейный угол этого двугранного угла.
2. ABCD – ромб.  А = 60°, АВ = m, BЕ
А = 60°, АВ = m, BЕ  АВС, BЕ =
АВС, BЕ = 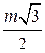 . Найдите угол между плоскостями AED и АВС.
. Найдите угол между плоскостями AED и АВС.
3. Через сторону ромба ABCD проведена плоскость α. Сторона АВ составляет с этой плоскостью угол 30°. Найдите угол между плоскостью ромба и плоскостью α, если острый угол ромба равен 45°.
Урок 18
ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ
Цель : ввести определение перпендикулярных плоскостей, доказать признак перпендикулярности плоскостей.
Ход урока
I. Объяснение нового материала построить в соответствии с пунктом 23.
Перед доказательством теоремы рассмотрите модели многогранников.
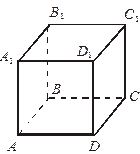
| 1. Плоскости (АВС) и (DD1C1) перпендикулярны. Докажите это. Каким свойством обладает прямая DD1 относительно указанных плоскостей? | |
|
| 2. ABCD – квадрат. FO  (АВС).
Докажите, что (AFC) (АВС).
Докажите, что (AFC)  (АВС).
Каким свойством обладает прямая FO относительно указанных плоскостей? (FO (АВС).
Каким свойством обладает прямая FO относительно указанных плоскостей? (FO  (AFC), FO (AFC), FO  (АВС).) (АВС).)
| |
Когда можно утверждать, что плоскости перпендикулярны? Выскажите предположение.
Сформулировать признак. Доказать.
II. Решение задач: №№ 177, 179, 181, 183, 184.
Домашнее задание: теория (п. 23), №№ 178, 180, 182, 185.
Урок 19
ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД
Цели : ввести понятие прямоугольного параллелепипеда; доказать свойство диагоналей прямоугольного параллелепипеда.
Ход урока
I. Проверка домашнего задания (признак).
II. Устная работа.
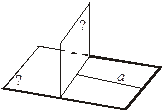
| 1. а  α, а α, а  β.
Докажите, что β β.
Докажите, что β 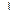 a. a.
|

| 2. β 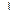 α, γ α, γ 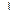 α, β α, β 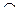 γ = АВ, d γ = АВ, d  α.
Докажите, что АВ α.
Докажите, что АВ 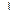 d. d.
|

| 3. 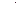 АВС = АВС = 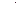 BCD, АВ BCD, АВ 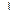 α.
Докажите, что:
1) CD α.
Докажите, что:
1) CD 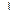 (АВС); 2) α (АВС); 2) α 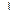 (АВС). (АВС).
|
4. Плоскость линейного угла двугранного угла перпендикулярна каждой его грани. Доказать.
Дата добавления: 2018-09-20; просмотров: 3837; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!