II. Проверка домашнего задания.
III. Устная работа.
1. Какие прямые называются скрещивающимися?
2. Сформулируйте признак скрещивающихся прямых.
3. Выясните взаимное расположение прямых:

| АD и В1С1; ВС и СС1; СС1 и АВ; СС1 и АА1; А1В1 и СD; MN и АВ; MN и А1В1; MN и АD; MN и В1С1. |
4. Верно ли утверждение: если две прямые не имеют общих точек, то они параллельны?
5. Две прямые параллельны некоторой плоскости. Могут ли эти прямые: а) пересекаться? б) быть скрещивающимися?
6. Могут ли скрещивающиеся прямые а и b быть параллельными прямой с? Ответ обоснуйте.
7. Даны две скрещивающиеся прямые а и b. Точки А и А1 лежат на прямой а, точки В и В1 – на прямой b. Как будут расположены прямые АВ и А1В1?
8. Прямая а скрещивается с прямой b, а прямая b скрещивается с прямой с. Следует ли из этого, что прямые а и с скрещиваются?
9. Каково должно быть взаимное расположение трех прямых, чтобы можно было провести плоскость, содержащую все прямые?
10. Можно ли провести прямую, пересекающую каждую из трех скрещивающихся прямых?
11. Даны две пересекающиеся плоскости α иβ. В плоскости α лежит прямая а, а в плоскости β – прямая b. Лежат ли прямые а и b в одной плоскости, если известно, что они пересекают линию пересечения плоскостей α иβ: а) в одной точке; б) в разных точках?
12. Даны две параллельные плоскости α иβ.В плоскости α лежит прямая а, а в плоскости β – прямая b. Каковы возможные случаи взаимного расположения прямых а и b?
|
|
|
13. В плоскости двух параллельных (пересекающихся) прямых а и b дана точка С, не лежащая на этих прямых. Прямая с проходит через точку С. Как может быть расположена прямая с относительно прямых а и b?
IV. Решение задач.
№ 39.

| Дано: АВ ¸ СD. Доказать, что AD ¸ BC. Доказательство 1. (A, C, D) = α. |
2. 
3. 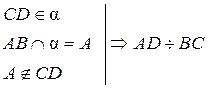 (по признаку).
(по признаку).
№ 41.
Дано: а ¸ b.
Может ли а || с и b || c.
Пусть а || с и b || c, тогда а || b. Противоречие условию.
№ 42.

| Дано: ABCD – параллелограмм, ABEK – трапеция, ЕK 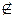 (ABC).
а) Выясните взаимное расположение прямых CD и ЕK.
б) Найдите РABEK, если АВ = 22,5 см, ЕK = 27,5 см, в трапецию можно вписать окружность. (ABC).
а) Выясните взаимное расположение прямых CD и ЕK.
б) Найдите РABEK, если АВ = 22,5 см, ЕK = 27,5 см, в трапецию можно вписать окружность.
|
1. 
2. Так как в трапецию можно вписать окружность, то АВ + ЕK =
= АK + ВЕ. РABEK = 2 ∙ (22,5 + 27,5) = 2 ∙ 50 = 100 см.
№ 43.

| Дано: ABCD – пространственный четырехугольник. М, N, Р, K – середины АС, АD, ВD, ВС соответственно.
Доказать, что MNPK – параллелограмм.
1. МK – средняя линия Δ АВС  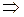 МK || АВ, МK = МK || АВ, МK =  АВ. АВ.
|
2. NP – средняя линия Δ АDB 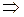 NP || АВ, NP =
NP || АВ, NP =  АВ.
АВ.
3.  – параллелограмм.
– параллелограмм.
№ 101.
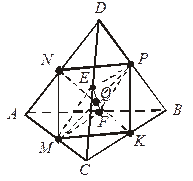
| Дано: ABCD – тетраэдр.
АМ = МС, AF = FB, AN = ND,
ВР = Р D, С K = K В, DE = Е C.
Доказать, что MP  NK NK  EF = Q.
Доказательство
1. MNPK – параллелограмм (см. № 43) EF = Q.
Доказательство
1. MNPK – параллелограмм (см. № 43)   MP MP  NK = Q, MQ = QP. NK = Q, MQ = QP.
|
2. MNPK – параллелограмм (аналогично)  МР
МР  EF = Q1, MQ1=
EF = Q1, MQ1=
= Q1Р.
3. 
4. MP  NK
NK  EF = Q.
EF = Q.
|
|
|
Домашнее задание: теория (п. 7), №№ 38, 93, 94, 100.
Урок 9
УГЛЫ С СОНАПРАВЛЕННЫМИ СТОРОНАМИ.
УГОЛ МЕЖДУ ПРЯМЫМИ
Цель : доказать теорему об углах с сонаправленными сторонами.
Ход урока
I. Повторение пройденного.
Продолжите предложение.
1. Если две прямые в пространстве не имеют общих точек, то они…
2. Если две прямые не принадлежат одной плоскости, то они…
3. Если ABCD – пирамида, то прямые АВ и СD…
4. ABCDA1B1C1D1 – куб. Прямые АВ и СС1…
5. Геометрическое место прямых, пересекающих одну из скрещивающихся прямых и параллельных другой, есть…
Дата добавления: 2018-09-20; просмотров: 935; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
