I. Проверка домашнего задания.
II. Устная работа.
1. Перечислите несколько способов задания плоскости.
2. Сколько плоскостей можно провести через выделенные элементы куба?
Заштрихуйте соответствующие плоскостям грани куба.
а) 
| б) 
| в) 
|
г) 
| д) 
| е) 
|
3. Сколько граней проходит через а) одну, б) две, в) три, г) четыре точки, выделенные на рисунке куба?
Сколько плоскостей можно провести через те же точки? Определится ли при этом положение плоскости однозначно? Ответ обоснуйте.
а) 
| б) 
| в) 
|
г) 
| д) 
| е) 
|
4. Если прямая пересекает две стороны квадрата (смежные, противоположные), то она лежит в плоскости этого квадрата?
5. Если две точки окружности лежат в одной плоскости, то и вся окружность лежит в этой плоскости?
6. Если два диаметра окружности принадлежат одной плоскости, то и вся окружность принадлежит этой плоскости?
| 7. ABCDA1B1C1D1 – куб. Верно ли, что плоскости (BCD1) и (B1C1D1) имеют одну общую точку? Назовите линию пересечения этих плоскостей. Через какую точку она проходит? | 
|
8. Найдите ошибку. Ответ обоснуйте.
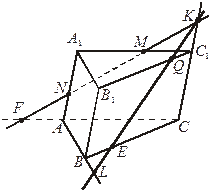
III. Решение задач.
Постройте изображение тетраэдра (треугольной призмы, четырехугольной пирамиды, четырехугольной призмы). Отметьте произвольно точки М, N, и К на ребрах многогранника. Постройте сечение многогранника плоскостью (MNK).
Домашнее задание аналогичное. Подготовить теорию к зачету (п. 1 – 3).
Урок 5
РЕШЕНИЕ ЗАДАЧ НА ПРИМЕНЕНИЕ
АКСИОМ СТЕРЕОМЕТРИИ И ИХ СЛЕДСТВИЙ
|
|
|
Цель : проверить знание учащимися аксиом стереометрии и их следствий и уровень сформированности навыка их применения при решении задач.
Ход урока
Вариант I
1. Точки А, В и С не лежат на одной прямой. М 
АВ, K АС, Х 
МK. Докажите, что точка Х лежит в плоскости (АВС).
2. Плоскости α и β пересекаются по прямой m. Прямая а лежит в плоскости α и пересекает плоскость β. Пересекаются ли прямые а и m? Почему?
| 3. Постройте: а) точки пересечения прямой EF с плоскостями (АВС) и (А1В1С1); б) линию пересечения плоскостей (EFK) и (АВС); в) сечение многогранника плоскостью (EFK). | 
|
Вариант II
1. Прямые а и b пересекаются в точке О. А а, В b; Y АВ. Докажите, что прямые а и b и точка Y лежат в одной плоскости.
2. Даны пересекающиеся плоскости α и β. Прямая а лежит в плоскости α и пересекает плоскость β в точке А. Прямая b лежит в плоскости βи пересекает плоскостьαв точке В. Докажите, что АВ – линия пересечения плоскостей α и β.
| 3. Постройте: а) точки пересечения прямой РМ с плоскостями (DCC1) и (AА1В1); б) линию пересечения плоскостей (MNP) и (АA1В1); в) сечение многогранника плоскостью (MNP). | 
|
ГЛАВА 2. ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ.
|
|
|
Урок 1
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ В ПРОСТРАНСТВЕ
Цели : рассмотреть взаимное расположение двух прямых в пространстве; ввести понятие параллельных и скрещивающихся прямых.
Ход урока
Дата добавления: 2018-09-20; просмотров: 1681; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!