Прямая и плоскость называются параллельными, если они не имеют общих точек.
Покажите на предметах обстановки классной комнаты прямые, параллельные плоскости пола, плоскости стены.

| На модели куба укажите плоскости, параллельные прямой DC, прямой DD1. Как установить параллельность прямой и плоскости? В силу бесконечности прямой и плоскости сделать это по определению очень трудно. Нужен признак параллельности прямой и плоскости. |
Обратите внимание на модель куба. DC || (АА1В1). В плоскости (АА1В1) имеется прямая AB, параллельная DC.
DC || (А1В1С1). В плоскости (А1В1С1) имеется прямая D1C1, параллельная DC. Сделайте предположение.
Сформулируйте и докажите признак параллельности прямой и плоскости.
II. Решение задач.

| № 22.
Дано: A 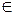 α, B α, B 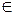 α, C α, C  α,
AM = MC, BN = NC.
Доказать, что MN || α. α,
AM = MC, BN = NC.
Доказать, что MN || α.
|
Доказательство


| № 24.
Дано: ABCD – трапеция,
М 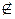 (АВС)
Доказать, что AD || (ВМС). (АВС)
Доказать, что AD || (ВМС).
|
Доказательство
 по признаку.
по признаку.
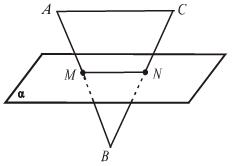
| № 26.
Дано: AC || α, AB  α= M,
CB α= M,
CB  α= N.
Доказать, что Δ ABC α= N.
Доказать, что Δ ABC 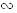 Δ MBN.
Доказательство
Докажем, что АС || MN. Δ MBN.
Доказательство
Докажем, что АС || MN.
|

2.  по определению.
по определению.
3. Δ АВС  Δ MBN по двум углам.
Δ MBN по двум углам.
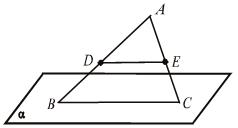
| № 28.
Дано: D  AB, E AB, E  AC, DE = 5, AC, DE = 5,
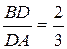 , BC , BC  α, DE || α.
Найдите ВС. α, DE || α.
Найдите ВС.
|
Решение

2.  по определению.
по определению.
3. Δ АВС 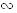 Δ ADE по двум углам.
Δ ADE по двум углам.
 .
.
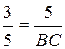 .
.
BC =  .
.
Домашнее задание: теория (п. 6), №№ 23, 25, 27.
Урок 5
ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ
Цель : продолжить формирование навыка применять изученные теоремы к решению задач.
Ход урока
I. Проверка домашнего задания (у доски).
II. Устная работа.
1. Каково может быть взаимное расположение прямой и плоскости в пространстве?
|
|
|
2. В каком случае прямая и плоскость называются параллельными? Пересекающимися?
3. Сформулируйте признак параллельности прямой и плоскости.
4. Верно ли утверждение, что если прямая, не лежащая в плоскости, параллельна ей, то она параллельна любой прямой, лежащей в этой плоскости?
5. Верно ли утверждение, что если две прямые параллельны одной и той же плоскости, то они параллельны между собой?
6. Можно ли построить плоскость, проходящую через данную прямую и параллельную другой данной прямой?
7. Сколько можно провести через данную точку:
а) прямых, параллельных данной плоскости;
б) плоскостей, параллельных данной прямой?
8. Каким может быть взаимное расположение двух прямых, из которых одна параллельна некоторой плоскости, а другая пересекает эту плоскость?
III. Решение задач.
Задача 1.
Доказать, что если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

| Дано: a || α, a  β, α β, α 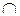 β = b.
Доказать, что а|| b.
Доказательство β = b.
Доказать, что а|| b.
Доказательство
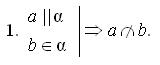
|
2.  по определению а || b.
по определению а || b.
Задача 2.
Доказать, что если через каждую из двух параллельных прямых проведена плоскость, причем эти плоскости пересекаются, то линия их пересечения параллельна каждой из данных прямых.
|
|
|

| Дано: a || b, a  α, b α, b  β,
α β,
α 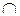 β = c.
Доказать, что а|| c и b || c.
Доказательство
1. β = c.
Доказать, что а|| c и b || c.
Доказательство
1. 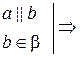 по признаку а || β. по признаку а || β.
|
2.  по предыдущему утверждению а || с.
по предыдущему утверждению а || с.
3. Аналогично, b || c.
Задача 3.
Доказать, что если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.

| Дано: a || b, a || α.
Доказать, что b || α либо b 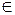 α.
Доказательство
Пусть b || α, следовательно b α.
Доказательство
Пусть b || α, следовательно b  α. α.
|
Тогда  по лемме a
по лемме a  α.
α.
Полученное противоречие опровергает предположение.
Задача 4.
Постройте сечение тетраэдра ABCD плоскостью, проходящей через вершину С, внутреннюю точку М ребра АВ и параллельной прямой AD.
Построение

| 1.  2.
2. 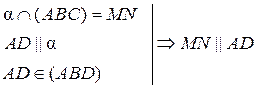
|
3. 
4. (MNC) – искомое сечение.
Найдите площадь полученного сечения, если каждое ребро тетраэдра имеет длину а и точка М является серединой ребра АВ.
№ 29.

| Дано: ABCD – трапеция,
ВС = 12 см, М 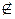 (АВС), ВK = KМ.
Доказать, что (ADK) (АВС), ВK = KМ.
Доказать, что (ADK)  МС = Н.
Найти KН.
1. МС = Н.
Найти KН.
1. 
|
2. 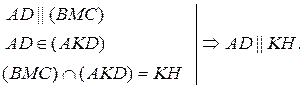
3. AD || BC, AD || KH  KH || BC.
KH || BC.
4. BK = KH, KH || BC  CH = HM.
CH = HM.
Следовательно, KН – средняя линия Δ BMC. KH = 6 см.
|
|
|
Домашнее задание.
№ 30.

| Дано: ABCD– трапеция,
AB || α, C  α.
Доказать, что:
CD α.
Доказать, что:
CD  α; MN || α, где MN – средняя линия трапеции. α; MN || α, где MN – средняя линия трапеции.
|
Доказательство
1. Пусть CD  α, тогда CD
α, тогда CD  α = c.
α = c.
 по лемме AB
по лемме AB  α. Но AB || α.
α. Но AB || α.
Полученное противоречие опровергает предположение.
Следовательно, CD  α.
α.
2.  по признаку MN || α.
по признаку MN || α.
№ 31.

| Дано: α || BC, AK = BK, K  α.
Доказать, что α α.
Доказать, что α  AC = M и AM = CM.
Доказательство
1. AC = M и AM = CM.
Доказательство
1. 
|
2. 
№ 32 (разобрать доказательство самостоятельно).
Урок 6
ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ,
ПРЯМОЙ И ПЛОСКОСТИ
Цели : систематизировать материал изученного параграфа; проверить уровень сформированности умения применять полученные знания к решению задач.
Ход урока
I. Проверка домашнего задания (у доски).
II. Устная работа.
1. Верна ли формулировка признака параллельности прямой и плоскости: «Прямая, параллельная какой-либо прямой на плоскости, параллельна и самой плоскости». (Нет, прямая может лежать в плоскости).
2. Прямые а и b параллельны. Какое положение может занимать прямая а относительно плоскости, проходящей через прямую b?
3. Даны прямая и две пересекающихся плоскости. Охарактеризовать все возможные случаи их взаимного расположения.
4. Одна из двух параллельных прямых параллельна некоторой плоскости. Можно ли утверждать, что и вторая прямая параллельна этой плоскости? Ответ обоснуйте.
|
|
|
5. Даны две пересекающиеся плоскости. Существует ли плоскость, пересекающая две данные плоскости по параллельным прямым?
6. Даны две скрещивающиеся прямые. Можно ли через одну из этих прямых провести плоскость, параллельную другой?
7. В плоскости α даны две пересекающиеся прямые а и b. Точка С не лежит в плоскости α. Каковы возможные случаи расположения прямой, проходящей через точку С, относительно прямых а и b?
8. Дано: FABCD – пирамида, ABCD – параллелограмм.

| Каково взаимное расположение прямой пересечения плоскостей (FAD) и (FBC) и плоскости основания (АВС)? |
III. Решение задач: №№ 90 (устно), 91, 92, 93, 96.
Домашняя контрольная работа
Вариант I
1. Через сторону АС треугольника АВС проведена плоскость α. В  α.Докажите, что прямая, проходящая через АВ и ВС, параллельна плоскости α.
α.Докажите, что прямая, проходящая через АВ и ВС, параллельна плоскости α.
2. Дан Δ MKP. Плоскость, параллельная прямой МK, пересекает МР в точке М1, РK – в точке K1. Найдите М1K1, если МР : М1Р = 12 : 5, МK = 18 см.
3. Точка Р не лежит в плоскости трапеции ABCD (AD || BC). Докажите, что прямая, проходящая через середины РВ и РС, параллельна средней линии трапеции.
Вариант II
1. Через основание AD трапеции ABCD проведена плоскостьα. ВС 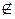 α. Докажите, что прямая, проходящая через середины сторон АВ и CD, параллельна плоскости α.
α. Докажите, что прямая, проходящая через середины сторон АВ и CD, параллельна плоскости α.
2. Дан Δ BCE. Плоскость, параллельная прямой СЕ, пересекает ВЕ в точке Е1, а ВС – в точке С1. Найдите ВС1, если С1Е1: СЕ = 3 : 8, ВС =
= 28 см.
3. Точка Е не лежит в плоскости параллелограмма АВСD. Докажите, что прямая, проходящая через середины АЕ и ВЕ, параллельна прямой СD.
Урок 7
СКРЕЩИВАЮЩИЕСЯ ПРЯМЫЕ
Цель : доказать признак скрещивающихся прямых, теорему о проведении через одну из скрещивающихся прямых плоскости, параллельной другой прямой.
Ход урока
I. Работа над ошибками.
II. Объяснение нового материала. Вспомнить различные случаи взаимного расположения прямых в пространстве (урок № 6).
Рассмотреть различные пары скрещивающихся прямых на моделях многоугольников, наблюдая факт, зафиксированный в признаке скрещивающихся прямых.

| Например, ABCDA1B1C1D1 – куб. АА1 и DC – скрещивающиеся ребра. В каких плоскостях лежит прямая CD? Как располагается прямая АА1 по отношению к этим плоскостям? |

| ABCA1B1C1 – призма. ВВ1 и А1С1– скрещивающиеся ребра. В каких плоскостях лежит прямая ВВ1? Как располагается прямая А1С1 по отношению к этим плоскостям? |

| АBCD – пирамида. Рассуждаем аналогично. Наблюдаем: прямые являются скрещивающимися, если одна прямая лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой. |
Если учащиеся упустили выделенный в формулировке факт, то привести контрпример – пересекающиеся прямые.
Доказать признак скрещивающихся прямых.
Для «открытия» учащимися факта второй теоремы опять обратиться к рассмотрению моделей, каждый раз отвечая на вопросы: назовите плоскость, проходящую через одну из скрещивающихся прямых параллельно другой прямой? Сколько таких плоскостей?
При рассмотрении третьей модели должна возникнуть проблема – можно ли через одну из скрещивающихся прямых построить плоскость, параллельную другой прямой? Учащимся предлагается построить такую плоскость.
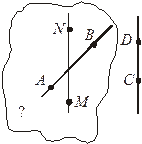
| Дано: AB  CD.
Построить α: АВ CD.
Построить α: АВ  α, СD || α.
Анализ
Предположим, что плоскость α построена. Тогда в ней найдется какая-либо прямая MN, параллельная прямой CD. Прямые АВ и MN пересекаются и однозначно определяют плоскость α. α, СD || α.
Анализ
Предположим, что плоскость α построена. Тогда в ней найдется какая-либо прямая MN, параллельная прямой CD. Прямые АВ и MN пересекаются и однозначно определяют плоскость α.
|
Построение
1. Построить MN  AB, MN || CD.
AB, MN || CD. 
2. (MN, AB) ≡ α.
3. α – единственная.
Таким образом, мы доказали теорему, что через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
III. Решение задач.
№ 34 (решать устно, требовать, чтобы учащиеся проговаривали формулировки признаков).
№ 36.
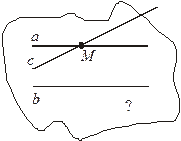
| Дано: a || b, c 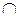 a, c a, c  b.
Доказать, что b b.
Доказать, что b  c.
Чтобы утверждать, что b и c – скрещивающиеся прямые, что надо доказать? (Что одна из них лежит в некоторой плоскости, а другая пересекает эту плоскость.) c.
Чтобы утверждать, что b и c – скрещивающиеся прямые, что надо доказать? (Что одна из них лежит в некоторой плоскости, а другая пересекает эту плоскость.)
|
Через какие прямые мы можем провести плоскость? (Через пересекающиеся, через параллельные.)
Если мы проведем плоскость α через пересекающиеся прямые а и с, то прямая b, будет параллельна плоскости α. То есть нужно провести плоскость αчерез параллельные прямые а и b.
1. (a, b) ≡ α.
2. 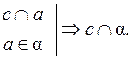
3. 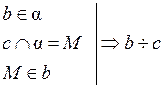 (по признаку).
(по признаку).
Домашнее задание: теория (п. 7), № 35 (воспользуйтесь методом от противного), № 37.
Урок 8
СКРЕЩИВАЮЩИЕСЯ ПРЯМЫЕ
Цель : закрепить навык использования признака скрещивающихся прямых при решении задач.
Ход урока
I. Опрос у доски (знание теорем, их доказательств).
Дата добавления: 2018-09-20; просмотров: 1357; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
