I. Проверка домашнего задания.

II. Устная работа.

1. Какие прямые в пространстве называются параллельными?

2. Всегда ли через две параллельные прямые можно провести плоскость? А через две непересекающиеся прямые?

3. В пространстве даны n параллельных между собой прямых. Известно, что никакие три из них не лежат в одной плоскости. Сколько различных плоскостей можно провести через эти прямые?

4. Сформулируйте лемму о пересечении плоскости параллельными прямыми.

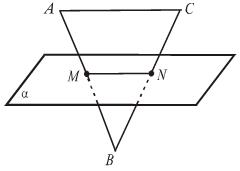
5. Отрезок, соединяющий середины двух сторон треугольника, лежит в плоскости α. Пересекает ли третья сторона эту плоскость?

6. Сформулируйте теорему о трех параллельных прямых.

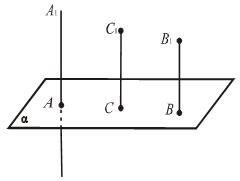
7. Дано: АА₁ || СС₁, АА₁ || ВВ₁, ВВ₁ = СС₁. Доказать, что В₁С₁ = ВС.

III. Решение задач.

Задача 1.

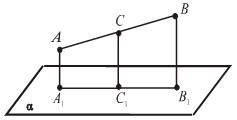
Дано: AB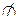

α, AC = CB, АА₁ || СС₁ || ВВ₁, АА₁= 5, ВВ₁ = 7. Найти СС₁.

Решение

I. Докажем, что точки A₁, C₁ и B₁ лежат на одной прямой.

1. (AA₁, BB₁) = β. β 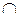α = A₁B₁. Докажем, что C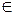₁ A₁B₁.

2. Пусть С₁ 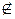А₁В₁, тогда CC₁ 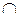β = C.

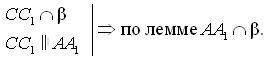
Полученное противоречие опровергает наше предположение.

Следовательно, С₁ А₁В₁.

3. СС₁ – средняя линия трапеции Þ CC₁ = 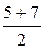= 6.

Задача 2.

Дано: AB α = D; AC = CB; АА₁ || СС₁ || ВВ₁; АА₁= 5; ВВ₁ = 7.

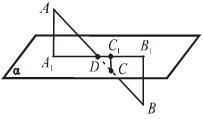
	Найдите СС₁. Решение I. Доказать, что точки А₁, С₁, D и В₁ лежат на одной прямой.
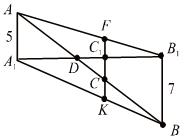
	II. 1-й способ. СС₁ – отрезок, соединяющий середины диагоналей трапеции. СС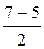₁ = = 1.

2-й способ.

СС₁ = C₁K – CK = 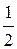BB₁ – 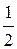AA₁ = 3,5 – 2,5 = 1.

Задача 3.

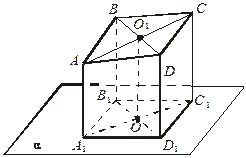
Дано: АВСD – параллелограмм, АА₁|| ВВ₁|| CC₁ || DD₁, АА₁ = 2, ВВ₁ = 3, СС₁ = 8. Найдите DD₁.

Задача 4.

Точка С лежит на отрезке АВ. Через точку А проведена плоскость, а через точки В и С – параллельные прямые, пересекающие эту плоскость соответственно в точках В₁ и С₁. Найдите длину отрезка ВВ₁, если:

а) СС₁ = 8,1, АВ : АС = 11 : 9;

б) АВ = 6, АС : СС₁ = 2 : 5;

в) АС = а, ВС = b, СС₁ = с.

Домашняя контрольная работа

Вариант I

1. Точки K, М, Р, Т не лежат в одной плоскости. Могут ли прямые KМ и РТ пересекаться? Обоснуйте ответ.

2. Через точки А, В и середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А₁, В₁, М₁ соответственно. Найдите длину отрезка ММ₁, если АА₁ = 13 м, ВВ₁ = 7 м, причем отрезок АВ не пересекает плоскость α.

3. Точка Р не лежит в плоскости трапеции АВСD с основаниями AD и ВС. Докажите, что прямая, проходящая через середины отрезков РВ и РС, параллельна средней линии трапеции.

Вариант II

1. Прямые ЕN и KМ не лежат в одной плоскости. Могут ли прямые ЕМ и NK пересекаться? Обоснуйте ответ.

2. Через концы А, В и середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А₁, В₁, М₁ соответственно. Найдите длину отрезка ММ₁, если АА₁ = 3 м, ВВ₁ = 17 м, причем отрезок АВ не пересекает плоскость α.

3. Точка Е не лежит в плоскости параллелограмма ABCD. Докажите, что прямая, проходящая через середины отрезков ЕА и ЕВ, параллельна стороне CD параллелограмма.

Урок 4
ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ

Цели : рассмотреть возможные случаи взаимного расположения прямой и плоскости в пространстве; ввести понятие параллельности прямой и плоскости; доказать признак параллельности прямой и плоскости.

Ход урока

I. Объяснение нового материала начать с рассмотрения взаимного расположения прямой и плоскости в пространстве.

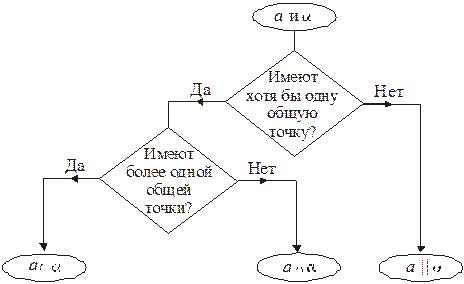
В каком случае прямая и плоскость называются параллельными?

Дата добавления: 2018-09-20; просмотров: 1025; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!