Приближенное интегрирование функций. Формула Симпсона и ее остаточный член.
При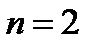 
из формулы 
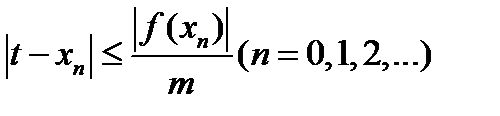(5.3) последовательно имеем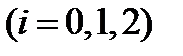 
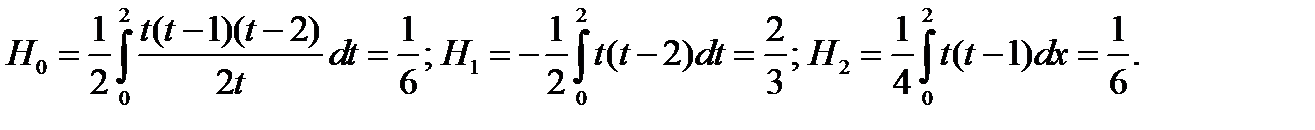
Тогда с учетом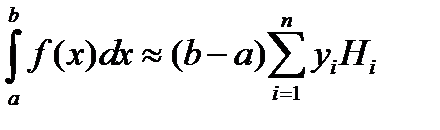 
(12.8) получим на отрезке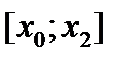 
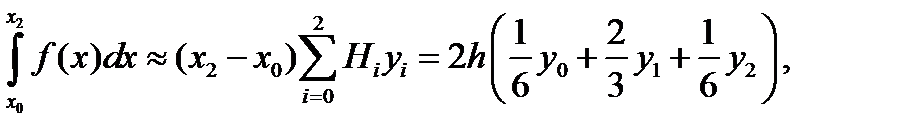т.е 
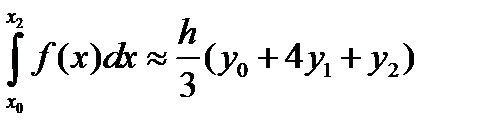. (12.17)
Геометрически, в соответствии со смыслом интерполяционной формулы Лагранжа при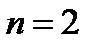 
, использование формулы (12.17) означает замену подынтегральной функцииf(x)параболой 
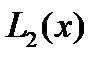, проходящей через точки 
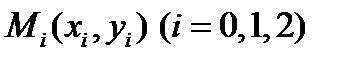(рис. 19).
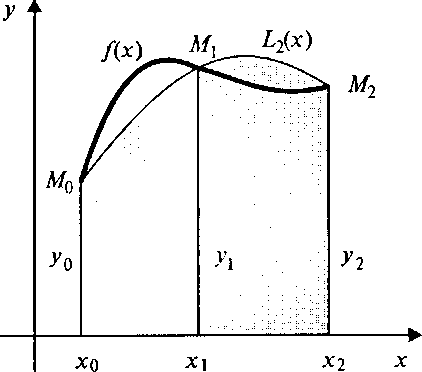Рис. 19. Иллюстрация к вычислению интеграла по формуле Симпсона
Если считать, чтоп — четное(п = 2т),то, применяя формулу (12.18) последовательнок каждой паре частичных отрезков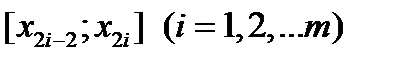 
, получим
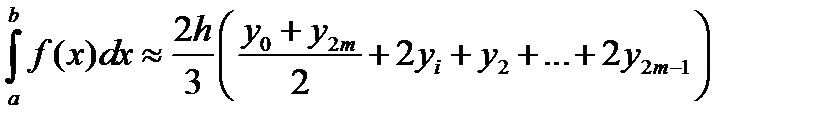(12.18)
Формула (12.18) называетсяформулой Симпсона
Оценку остаточного члена формулы Симпсона приведем без вывода: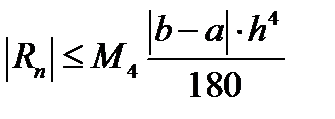 
(12.19), где 
.
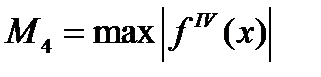Как следует из оценки, формула Симпсона оказывается точной для полиномов до третьей степени включительно (так как для этих случаев производная четвертого порядка равна нулю).
Укажем в заключение весьма простой практический прием, позволяющий прогнозировать требуемое число отрезков разбиения по заданной точности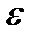 
.
Пусть задана предельная допустимая погрешность интегрирования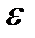 
. Желая иметь 
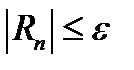с учетом оценки (12.19) достаточно потребовать: 
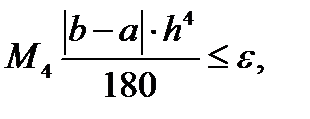откуда 
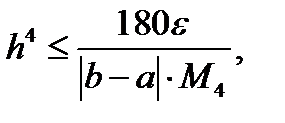т.е.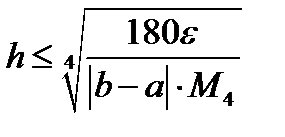 
(12.20)
|
|
Формула (12.20) позволяет оценить величину шага, необходимую для достижения заданной точности (из формулы видно, чтоhимеет порядок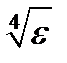 
).
Приближенное интегрирование функций. Оценка погрешности квадратурных формул (метод пересчета).
|
|
|
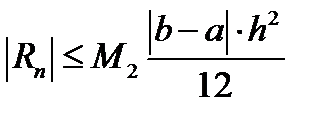(12.16) и 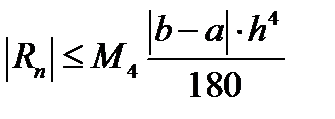(12.19),
Пусть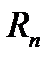 
и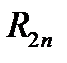 
— погрешности интегрирования по формуле 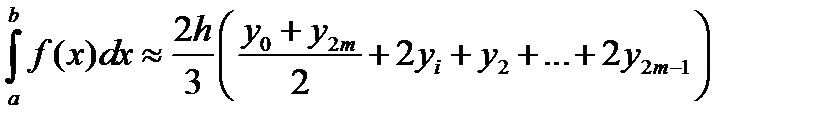Симпсона, соответственно прип и 2п отрезках разбиения. Учитывая (12.19), можно составить приближенную оценку 
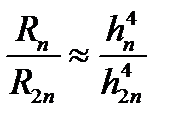(12.21),
где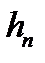 
и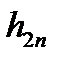 
— длина отрезков разбиения (шаг интегрирования) в первом и втором случае. Понятно, что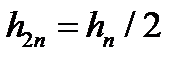 
Из (12.21) получаем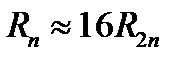 
(12.22).
Если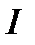 
— истинное значение интеграла, то 
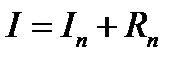и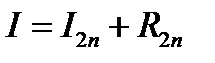 
,откуда с учетом (12.22) 
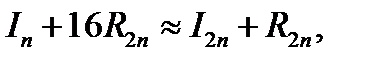т.е.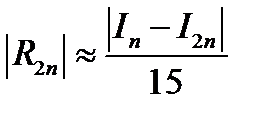 
(12.23)
Формула (12.23) удобна для практической оценки погрешности метода Симпсона, но требует двойного счета.
Аналогичное рассуждение применительно к методу трапеций приводит к оценке
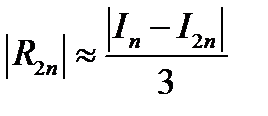(12.24) .
Из оценочных формул (12.16) и (12.19) следует, что ошибка интегрирования по методу трапеций и методу Симпсона уменьшается с уменьшением шага интегрирования (для метода Симпсона — значительно быстрее). На основании этого можно сделать вывод: при последовательном увеличении числа отрезков разбиения значение интеграла будет приближаться к точному. Однако это утверждение имеет чисто теоретическое значение. Дело в том, что в процессе практических вычислений при последовательном удвоении числа отрезков разбиения начинает сильно прогрессировать удельный вес ошибки округления, значение которой с некоторого момента ставит предел реально достижимой точности результата интегрирования.
|
|
|
Дата добавления: 2018-08-06; просмотров: 370; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!