Приближ.реш. СЛУ. Постановка задачи. Метод итерации. Дост.усл.сходимости
Дана n линейных алгебраических уравнений с n неизвестными:
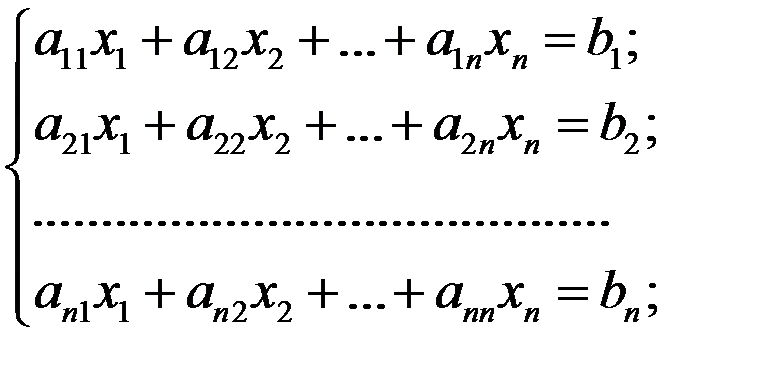(3.1) Приведем систему (3.1) к равносильной ей системе вида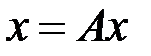 
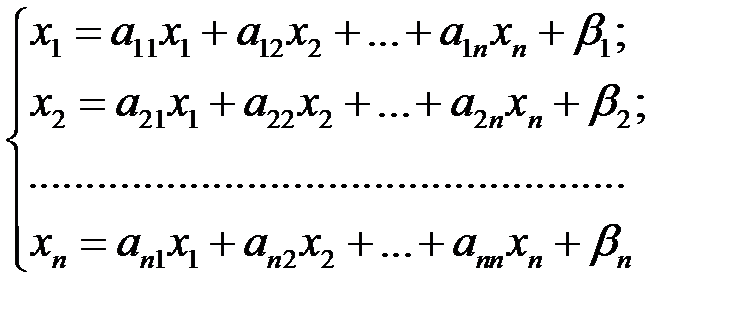(3.2)
в сокращенной записи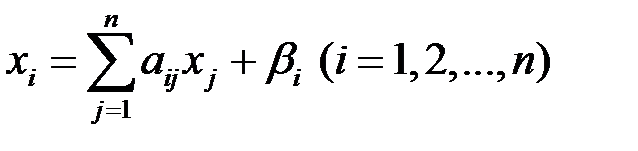 
(нормальный вид)
Пр.часть системы (3.2) определяет отображение :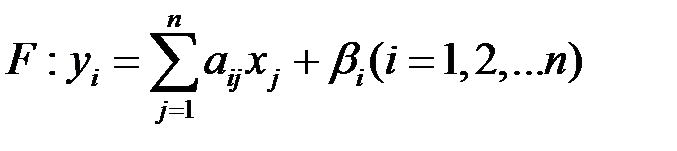 
(3.3)
преобразующее точку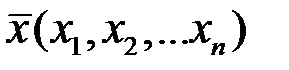 
-мерного векторного пространства в точку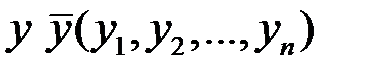 
того же пространства. Исп-я отображение (3.3) и выбрав нач.т . 
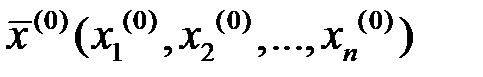, можно построить итерационную послед-ть точек 
-мерного пр-ва:
(3.4)
Напр: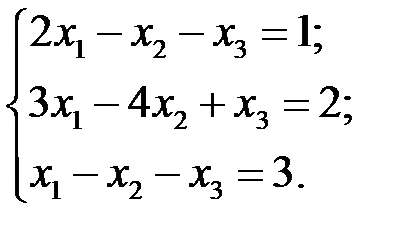 
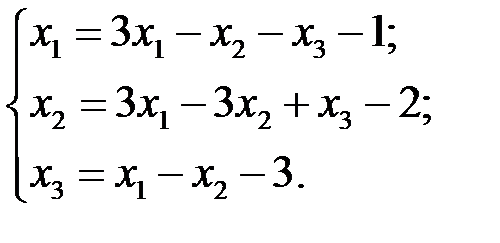
Нач. приближение, т. (0; 0; 0) трехмерного пр-ва, подставим ее в пр. ч системы. Получим коорд.т (-1; -2; -3). Исп. эту точку как нач-ю, получим след. т (1; -2; -2) и т.д.
Если отображение является сжимающим отображением, то эта последовательность сходится и ее предел является решением данной системы и тем самым исходной системы.
ОП. отображение F называется сжимающим, если сущ такое число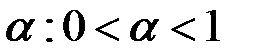 
, что для любых двух точек 
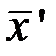и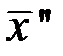 
вып. усл 
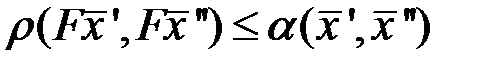. Рассмотрим условия, при которых отображение (3.3) будет сжимающим.
Пусть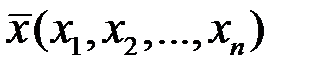 
и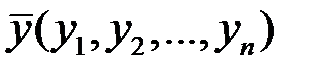 
— две точки 
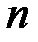-мерного пространства. Для применения метода итерации систему линейных уравнений удобно «погрузить» в пр-во с одной из трех следующих метрик:
а)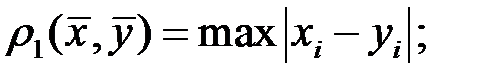 
(3.5)
б) 
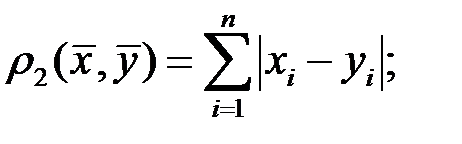(3.6)
в)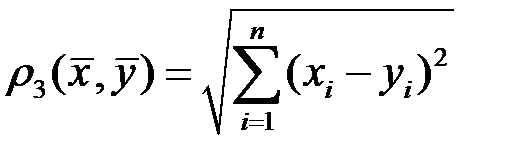 
. (3.7)
|
|
|
Условие сходимости итер процесса.Т1: если для приведенной системы (7) выполнено хотя бы одно из условий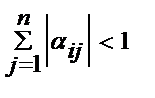 
(i=1..n)или 
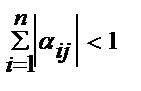(j=1..n), то итерационный процесс сходится к единств реш этой системы независимо от выбора начального приближения. Для системы A*x=b метод итерации сходится, если выполнено условие 
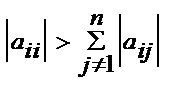i=..n (j=1..n).
Т2:Процесс итерации для приведенной системы (7) сходится к единств. ее решению, если какая-нибудь каноническая норма матрицы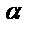 
<1,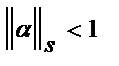 
,где s={m,l,k} где 
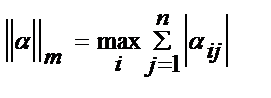(строки), 
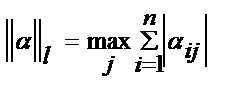(столбцы) 
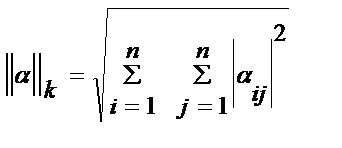(все эл-ты суммируются).
Условия (3.8) —(3.10) легко вывести.
Для точек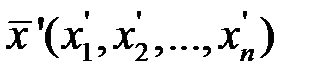 
и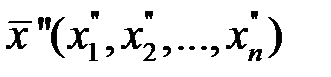 
в соответствии с (3.8) имеем:
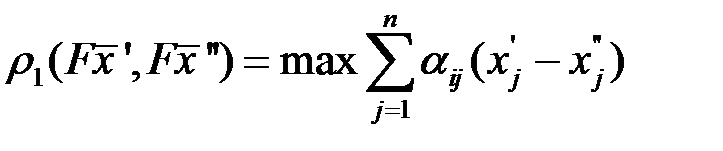(3.12)
По свойству абсолютной величины имеем: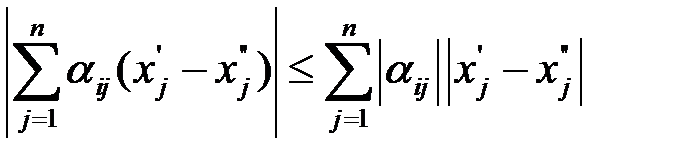 
Это нер-во лишь усилится, если заменить каждый модуль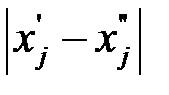 
значением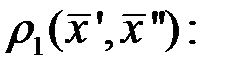 
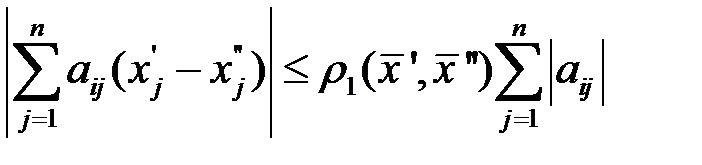
Подставляя это в (3.12), получим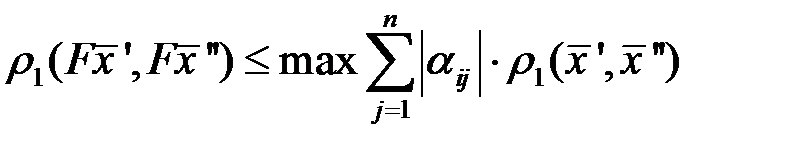 
(3.13)
Сравнивая (3.13) с (3.11), получаем условие (3.8).
Итак, для применения метода итераций система (3.1) должна быть переписана в виде (3.2). Гарантией сходимости итерационного процесса может служить выполнение хотя бы одного из достаточных условий (3.8) — (3.10). Для обеспечения условий сходимости нужно получить систему вида (3.2) так, чтобы коэффициенты при неизвестных были существенно меньше единицы. Этого можно достичь, если исходную систему с помощью равносильных преобразований привести к системе с преобладающими диагональными коэффициентами, т.е. у которой абсолютные величины коэффициентов, стоящих на главной диагонали, больше абсолютных величин остальных в соответствующих уравнениях. Если потом разделить все уравнения на соответствующие диагональные коэффициенты и выразить из каждого уравнения неизвестное с коэффициентом, равным единице, то будет получена система вида (3.2), у которой все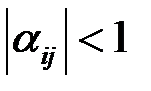 
. Выполнение этого условия необходимо, но не достаточно для выполнения условий сжимаемости (3.8) — (3.10).
Дата добавления: 2018-08-06; просмотров: 400; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!