ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ. ФОРМУЛЫ ЛАГРАНЖА.

Интерполяционный многочлен Лагранжа

Пусть функция F(x)задана табл.1 .

				...
F(x)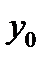

Построим многочленL_n(x), степень которого не выше, чем , и для которого выполнены ус­ловия интерполяции .(1). Будем искать в виде ,(2)где  — многочлен степени , причем

 (3).

Очевидно, что требование (3) с учетом (2) вполне обеспе­чивает выполнение условий (1). Многочлены  составим следующим образом: (4), где  — коэффициент, значение которого найдем из первой ча­сти условия (3):

 (заметим, что ни один множитель в знаменателе не равен нулю). Подставим в (4) и далее с учетом (2) окончательно имеем: .(5)

Это и есть интерполяционный многочлен Лагранжа.

Организация ручных вычислений по формуле Лагранжа

В табл. 1 показано построение такой схемы для 4 узлов 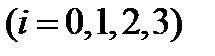 Таблица составляется заново для каждого нового значе­ния аргумента .

Заполнение таблицы начинается с того, что вычисляются и заносятся в соответствующие клетки все элементарные разности. Вслед за этим вычисляются произведения разностей по стро­кам:

Табл.1 ;

. С учетом этого обозначения формула Лагранжа имеет вид .Все необходимые значения последовательно получаются в таб­лице. Сумма 5 образуется сложением элементов последнего столб­ца. Для получения окончательного значения  достаточно ум­ножить S на произведение  (произведение диагональных разностей таблицы).

Приближенное интегрирование функции. Квадратурные формулы Ньютона-Котеса.

При вычис-ии опр-го интеграла , где  непр. на отрезке [a;b] ф-я, иногда удается практич. воспользоваться формулой Н-Л: 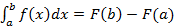(5.1) . Здесь одна из перво-зных фу-ий.

Эта формула не исчерпывает практ-их приемов вычисл-ия , так как:

1) Первооб-ую не удается явно найти в аналитической форме,

2) Первооб-ую удается найти в аналит-ой форме, но не удается довести до число-го отв-та значение опр-го .

3) иногда подынтегральная ф-ия задается табл-ей или граф-ом.

Поэтому часто примен. раз-ные методы  (числ-ого)

Опр. Формулы, исполь-мые для  выч-ния , наз-ют квадр-ми фор-ми.

Простой прием постр-ия квадр-ных формул состоит в том, что подынтег-ная ф-я замен-тся на отрезке [a;b] интерпол-ным мн-ом, напр. мн-ом Лагр-жа ,и принимается равенство

При этом предполагается, что отрезок [a;b] разбит на п частей точками 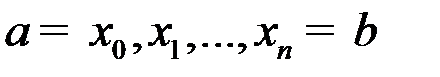, наличие к-х подразум-тся при постр-и мн-на . В силу (!) интер-ого полинома n-й степ. для данной ф-и и данной системы узлов не имеет значения, исп-ть ли в этой процедуре мн-ен Лаг-жа или мн-ны Нью-на.

Подставляя в (5.2) вместо его предст-ние, получим

 

ТО, (5.3),где (5.4)

По полученным формулам:

1. коэф-ты не зависят от вида ф-иf(x),т.к они сост-ны только с учетом узлов интер-ции;

2. еслиf(x) — полином степ. n, то тогда формула (5.3)-точная, иначе в этом случаеL(x) = f(x).

---

Дата добавления: 2018-08-06; просмотров: 355; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!