Приближенное решение нелинейных уравнений .Метод итерации. Оценка погрешности метода итерации.
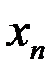- приближение к истинному значению корня уравнения 
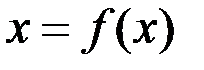. Абсолютная ошибка приближения 
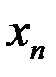оценивается модулем: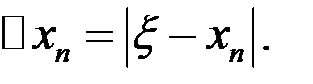 
Принимая во внимание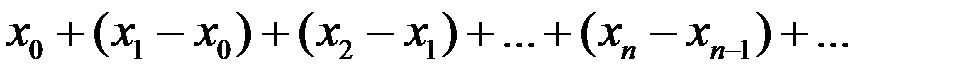 
и 
, и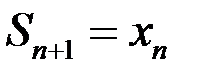меем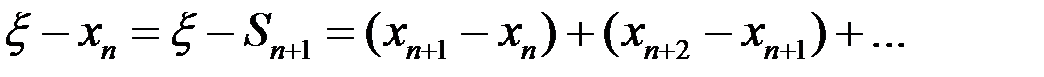 
Сравним данный ряд с остатком ряда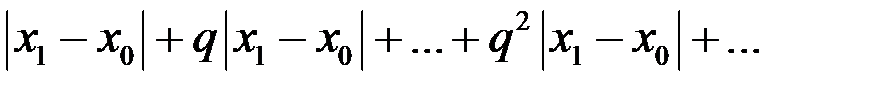 
:
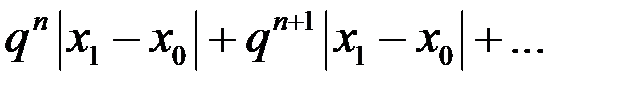
Ввиду оценок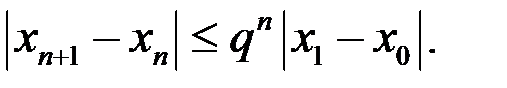 
, имеем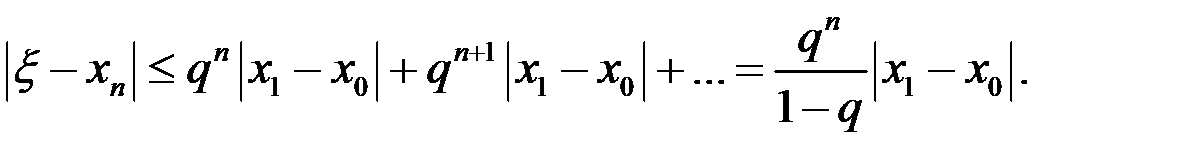 
Т.о. для оценки погрешности n-го приближения получаем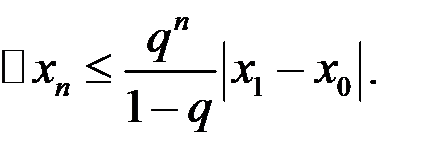 
На практике используют модификацию этой формулы. Принимают за нулевое приближение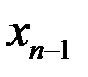 
. Вместо 
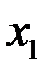принимают тогда 
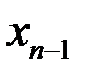. Учитывая также, что при 
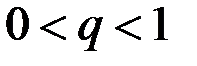будет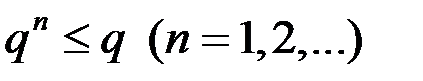 
, получаем: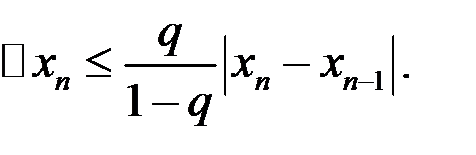 
Критерием для прекращения вычислений при достижении заданной точности служит неравенство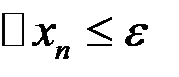 
. Учитывая полученную оценку, достаточно потребовать
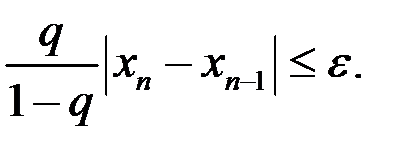Откуда 
.
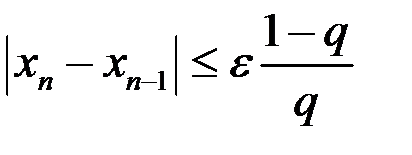Для достижения заданной точности, нужно продолжить итерации до тех пор, пока модуль разности между последними соседними приближениями остается больше числа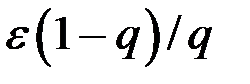 
.Схема решения.
Приближенное решение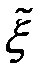 
и погрешность приближения 
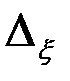находятся по следующей схеме:
1. Выполнить отделение корней. Выбрать тот корень, который подлежит уточнению, и соответствующий ему отрезок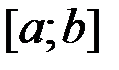 
, содержащий этот корень и не содержащий иных корней данного уравнения.
2. Преобразовать уравнение F(x)=0 к равносильному ему ур-ию вида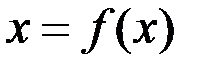 
, где ф-я 
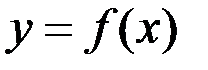удовлетворяет условиям: 
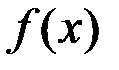Î[a,b], дифференцируема на отрезке и 
.
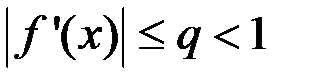3. Задаться 1-ым членом итерационной последовательности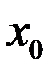 
— начальным приближением к корню; например, 
;
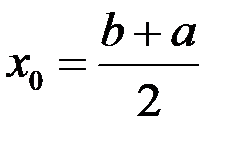4. Построить остальные приближения итерационной последовательности
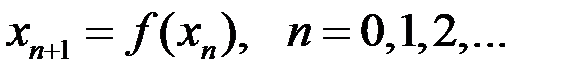
5. Всякий раз, получив очередной член итерационной последовательности, проверять, выполняется ли условие:
|
|
|
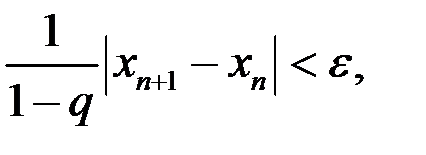или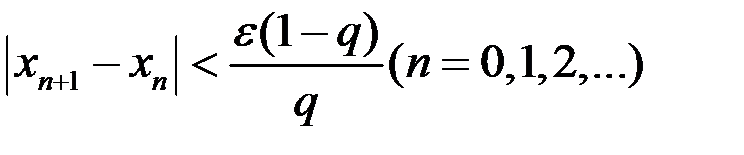 
.
6. Если условие п.5 выполняется, то принять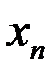 
за результат, иначе выполнить п.4.
Численное решение СЛУ. Постановка задачи.Метод Гаусса,ф-лы Крамера.
Число неизв-х в системе м/б больше числа ур. или равно ему. Если число неизв-х больше числа ур,то на 1-ом этапе алгебраич-ми методами задача сводится к промежуточной задаче,в которой число неизв-х равно числу уравнений. Дана система nлин.алгебр-х ур-й с n неизвест-ми:
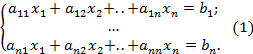
Будем исп-ть матричную форму записи,равносильную: Ax=b.
Методы реш-я СЛУ вида (1) м/о разделить на 2 класса: 1) точные методы. С помощью таких методов м/о в резул-те конеч.ч-а шагов получить точные знач-я неизвестных. При этом предполагается,что и коэф-ты в прав. части,и элементы столбца своб.членов-ч-а точные,а все вычис-я производятся без округлений. К подобным методам относятся:
· Метод определителей(метод Крамера);
· Матричное реш-е: x=A-1b (если известна обрат.матрица);
· Различ.варианты метода исключения неизв-ых(метод Гаусса).
2 класс: различные итерац.методы.
Метод Гаусса. Метод,основанный на схеме !-го деления. Суть метода Гаусса состоит в преобразовании системы (1) к равносильной ей системе с треугольной матрицей,из которой затем последовательно получаются знач-я всех неизв-х. метод Гаусса относится к точным методам. Подвергенем сист. (1) след-му преобраз-ю. считая что a11не = 0, разделим на 11 коэф-ты 1го ур-я: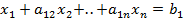 
. Над остальными ур-ми систем совершим аналогич-е преобраз-е. в рез-те получим равносильную ей сист. С треуг.матрицей:
|
|
|
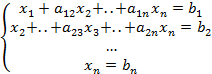(3)
Из получ-й сист. последов-но находят знач-я неизвест-х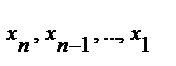 
. Т.о.,процесс реш-я сист.(1) по методу Гаусса распадается на 2 этапа. Первый этап,сотоящий в последовательном исключ-и неизвест-х,называют прямым ходом. Второй этап вычислений-нахождение знач.неизвестных-принято наз-ть обратным ходом.
Формула Крамера: основан на использовании определителей в решении CЛУ. Определитель, составленный из коэфф-ов при неизвестных, называется определителем системы и обозначается Δ,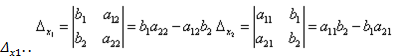 
Пусть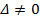 
тогда, 
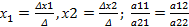,. Если коэффициенты при переменных пропорциональны то такая система имеет ед. решение.
Пусть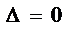 
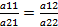Если коэфф-ты при переменных пропорциональны, то эта система либо имеет 
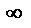много решений, либо не имеет решений вообще.
1) 
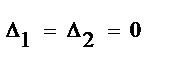Следовательно 
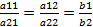. Если коэфф. при пер-х и свободных коэффициентах пропорц., то система имеет 
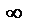много решений.
2) 
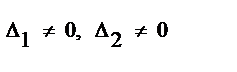
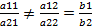Если отношение при пер-х не равно отношению свободных коэфф., то такая система несовместна
Дата добавления: 2018-08-06; просмотров: 633; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!