Оценка погрешностей приближений.
Приближения 
найденные методом хорд, стремятся к неизвестному корнюt с одной стороны. Поэтому так же легко, как в методе половинного деления, проверять условие окончания итерационного процесса здесь не удастся. Необходимы специальные формулы оценки сверху расстояния 
.
Теорема: Пусть корень t уравненияf(x)=0 отделен на отрезке 
, и все члены некоторой последовательности 
приближений к tрасположены в этом отрезке. Если производная 
конечна на 
и существует такое число m> 0, что 
для всех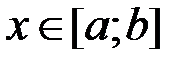 
, то имеет место неравенство:
(2.4.3)
Доказательство: Возьмем произвольное 
По теореме Лагранжа найдется такая точка с между хп иt, что 
. Так какt — корень, то 
и потому 
. Осталось сослаться на то, что 
.
Теорема 2:Пусть первая и вторая производные функции 
уравнения (2.1.1) непрерывны и сохраняют постоянный знак на отрезке 
изоляции, а числа m и М такие, что 
. Тогда погрешности приближений к t, найденных методом хорд, оцениваются формулой
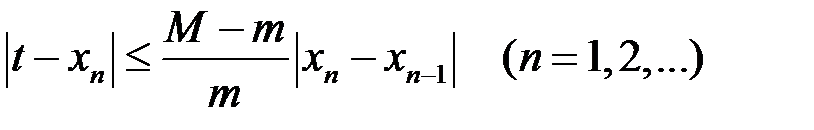
Т.о., если задана абсолютная погрешность 
, то процесс останавливается при выполнении одного из неравенств:
Приближенное решение нелинейных уравнений. Метод касательных.
Пусть дано уравнение: 
, корень t которого отделен на отрезке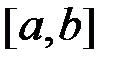 
. Функция fимеет непрерывные производные 
и 
с отличными от нуля и сохраняющими постоянный знак значениями при всех 
.
|
|
|
Будем считать, что известно какое-то приближение 
(например, начальное приближение 
). Тогда по формуле Тейлора (с остаточным членом в форме Лагранжа) междуtихп найдется точкасп такая, что
Если 
достаточно близко к t, то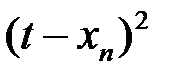 
мало, поэтому третье слагаемое можно отбросить и получить приближенное равенство: 
Отсюда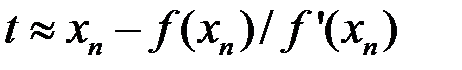 
. Получилось новое приближение кt, которое примем за 
. Таким образом, 
(2.5.1)
Геометрический смысл метода заключается в том, что приближения по нему равны абсциссам точек пересечения оси Ox и касательных к графику функцииу= f(x).
Покажем, что это действительно так, взяв случай 1, когда 
на [a; b]. Возьмем 
и проведем касательную к графику функции в точке 
Ее уравнение: 
Схема применения метода касательных.
Касательная пересечет ось Ох при у = 0. Подставив у= 0 в уравнение, получим абсциссу точки пересечения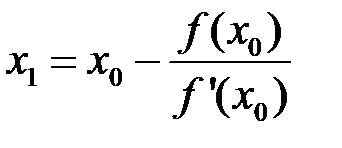 
.
Записав уравнение касательной к графику в точке 
при у =0 получим 
и т.д. Для любых n получаем выражение
Видим, что каждый раз абсциссы точек пересечения касательных с осью Ох вычисляются по формуле , причем всегда 
Правило выбора начального приближения:
|
|
|
Если 
на 
(случаи 1-2), то 
, иначе если 
(случаи 3-4), то 
.
Схемы применения метода касательных для всех случаев.
Оценка погрешностей приближений
Теорема: Пусть первая и вторая производные функции 
уравненияF(x)=0 непрерывны и имеют постоянный знак на отрезке 
изоляции корня t. Пусть положительные числа m и 
таковы, что 
.Тогда погрешности приближений к t, найденных методом касательных, оцениваются формулой
Доказательство. При соответствующем выборе начального приближения 
все приближения 
, вычисленные по формуле 
находятся на отрезке 
. По формуле Тейлора при некотором 
между 
и 
| имеем 
(2.5.3). Переписав формулу для вычисления хп в виде равенств 
из (2.5.3) и условий теоремы получим 
. Из формулы с учетом данного неравенства следует доказываемая оценка.
Дата добавления: 2018-08-06; просмотров: 470; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!