Квадратурные формулы Ньютона-Котеса
Формула 
для «весовых» коэффициентов 
принимает вид
(5.5). Перейдем в этом 
всюду к переменной 
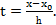Получаем: 
, т.е. 
.При 
имеем 
, а при 
будет
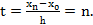Тогда 
, (5.6), где 
. (5.7) Числа Hiназывают коэф-ми Котеса. Как видно, коэф-ты Котеса не зависят от вида ф-и 
, а только от числа п точек разбиения. Окончательно с учетом формул (5.2). и (5.5) получаем след. вид квадр-ых формул Н-К: 
, (5.8) дающих на одном участке интег-ия разл. предстия для разл. числа n отрезков разбиения.
Приближенное интегрирование функции. Формулы левых и правых прямоугольников. Оценка погрешностей.
Итак, требуется вычислить определённый интеграл: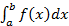 
. ┘ задана ф-я 
непр. на отрезке [a,b]. Разделим отрезок [a,b] точками a=x0, x1, x2,…, xn=b на n равных частей длины Δх, где Δх=(b-a)/n. В данном способе подынт-ая ф-я замен-тся ф-ей, к-я имеет ступенчатый вид (см рис.5.3).
| b=xn |
| a=x0 |
| x1 |
| y0 |
| y1 |
| yn |
| y=f(x) |
Рис 5.3. Применение метода прямоугольников.
Составим суммы: y0Δx+ y1Δx1+ y2Δx2…+yn-1Δxи y1Δx+ y2Δx+…+ynΔx.
Каждое слаг-ое этих сумм выражает S, полученных прямоуг-ов с основанием Δх, которое является шириной прямоуг-ка, и длиной, выраженной ч\з yi.
Каждая из этих сумм является 
суммой для f(x) на отрезке [a,b], и равна S ступ-х фигур, а значит 
вычисляет 
. Вынесем Δx=(b-a)/n из каждой суммы, получим: 
(5.21) 
(5.22)
Это и есть формулы □-ов. 1-я формула наз-ся формулой метода лев. □, а 2 – ф-ой метода прав. □.
Оценка погрешности.
|
|
|
Погрешности формул (5.21) и (5.22) оцениваются одинаково, поэтому далее правые части этих формул 
и их остаточные члены 
(i=1,2) для простоты будем записывать без верхних индексов. Дадим без доказательства формулу погрешности.
Т. Если подынтегральная функция f имеет на [a;b] непрерывную производную f', то оценка погрешности формул (5.21) и (5.22) дается равенством:
, (5.24) где 
.Как видно из выражений 
, оценка погрешностей формул прямоугольников зависит от подынтегральной функции, от величины отрезка интегрирования и количества n разбиений отрезка.
Формула средних прямоугольников. Оценка погрешности.
Пусть функция 
определена и интегрируема на отрезке 
. Необходимо найти значение определенного интеграла 
.
Для применения методов численного интегрирования делят отрезок 
системой равноотстоящих точек 
, 
, 
, 
, 
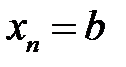на отрезки 
, 
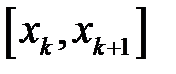и рассматривают сумму интегралов 
.
В этом случае 
на отрезке 
заменяется функцией 
, тогда
,
, 
.
Графическая иллюстрация метода средних прямоугольников представлена на рис. Из рисунка видно, что площадь криволинейной трапеции приближенно заменяется площадью многоугольника, составленного из N прямоугольников. Таким образом, вычисление определенного интеграла сводится к нахождению суммы N элементарных прямоугольников.
|
|
|
19. Формула трапеции и ее остаточный член
При 
из формулы 
имеем
Тогда по формуле 
на отрезке 
получаем интеграл
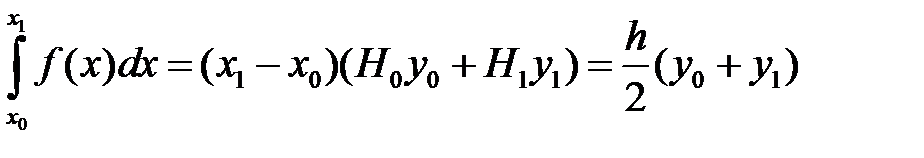(5.9)
Формула (5.9) называется формулой трапеций. При 
подынтегральная функция заменяется интерполяционным многочленом Лагранжа первой степени (т.е. линейной функцией), а геометрически это означает, что площадь криволинейной фигуры подменяется площадью трапеции (рис. 18).
Распространяя формулу (5.9) на все отрезки разбиения, получим общую формулу трапеций для отрезка 
(5.10)
Рис. 18. Иллюстрация к вычислению интеграла по формуле трапеций
Вид формулы для оценки погрешности метода интегрирования по формуле трапеций
(5.16)
Дата добавления: 2018-08-06; просмотров: 417; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!