Приближенное решение нелинейных уравнений. Комбинированный метод.
В методах хорд и касательных приближения «подходят» к корню только с одной стороны, что затрудняет оценку их погрешностей. Однако если эти методы применять не раздельно, а в сочетании друг с другом, то от этого недостатка можно избавиться.
В каждом из случаев относительно знаков  и
и  последовательные приближения рассматриваемых методов находятся по разные стороны от корня. Если обозначить приближения метода хорд через
последовательные приближения рассматриваемых методов находятся по разные стороны от корня. Если обозначить приближения метода хорд через 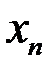 приближения метода касательных через
приближения метода касательных через  , то всегда выполняется
, то всегда выполняется  или
или  .
.
Тогда, как и в методе половинного деления, корень будет находиться в каждом из вложенных отрезков с концами 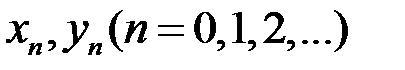 , причем
, причем  при
при  . Отрезки стягиваются к корню t, поэтому процесс уточнения с точностью до
. Отрезки стягиваются к корню t, поэтому процесс уточнения с точностью до 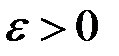 можно остановить сразу же, как только окажется
можно остановить сразу же, как только окажется  , и взять в качестве приближенного корня середину отрезка между
, и взять в качестве приближенного корня середину отрезка между  и
и 
Когда вычисления ведутся без заданной степени точности и на некотором шаге  в качестве прибл-я к корню выбрана средняя точка
в качестве прибл-я к корню выбрана средняя точка  между
между 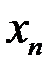 и
и  тогда
тогда  .
.
Процесс уточнения будет более быстрым, если для вычисления  методом хорд вместо соответствующего неподвижного конца отрезка
методом хорд вместо соответствующего неподвижного конца отрезка  использовать найденное методом касательных приближение
использовать найденное методом касательных приближение  т.е. когда хорды проводятся через точки графика функции с абсциссами
т.е. когда хорды проводятся через точки графика функции с абсциссами 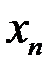 и
и 
Именно при таком способе вычислений есть смысл говорить окомбинированном методе хорд и касательных.
Рассмотри случай при  на
на 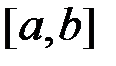 (случай 1).
(случай 1).  Из сказанного понятно, что вычисление пары чисел
Из сказанного понятно, что вычисление пары чисел 
 надо начинать с
надо начинать с  , которое определяется по-прежнему формулой метода касат:
, которое определяется по-прежнему формулой метода касат: 
|
|
|
при соответствующем начальном приближении  . Затем по формуле хорд отыскивается
. Затем по формуле хорд отыскивается  :
:  ,
,
При этом благодаря комбинированию методов его вычисление упрощается, поскольку формула метода хорд становится единой, не зависящей от знаков производных.
Напомним еще разправила выбора начальных приближений:
Если  на
на  (случаи 1-2), то
(случаи 1-2), то  ,
,  , иначе, если
, иначе, если  (случаи 3-4), то
(случаи 3-4), то  ,
,  .
.
Ниже приведены схемы применения комбинированного метода для всех 4-х случаев.




Приближенное решение нелинейных уравнений. Метод итерации .Достаточное условие сходимости.
Постановка задачи. Дано нелинейное уравнение F(x)=0 (2.1),где функция y=F(x) определена и непрерывно-дифференцируема для всех  , причем корень
, причем корень  отделен на отрезке [a,b].
отделен на отрезке [a,b].
Необходимо уточнить данный корень  с точностью
с точностью  .
.
Пусть F(x)=0 приведено к равносильному виду  (2.2).
(2.2).
Заменить  равносильным уравнением
равносильным уравнением 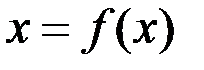 можно множеством способов. Простой — добавить х к левой и правой частям F(x)=0.
можно множеством способов. Простой — добавить х к левой и правой частям F(x)=0.
Пусть  — корень уравнения
— корень уравнения  , a
, a  — полученное каким- либо способом на этапе отделения корней грубое приближение к корню. Подставляя
— полученное каким- либо способом на этапе отделения корней грубое приближение к корню. Подставляя  в правую часть (2.2), получим число
в правую часть (2.2), получим число  . Проделаем то же самое с
. Проделаем то же самое с  получим
получим 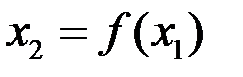 и т.д. Последовательно применяя рекуррентное соотношение
и т.д. Последовательно применяя рекуррентное соотношение  для
для  образуем итерационную послед-ть
образуем итерационную послед-ть 
|
|
|
(слово «итерация» - повторение (лат. iteration)). Процесс построения итерационной последовательности имеет простую геометрическую интерпретацию:

Рис. Построение итерационной последовательности

На рис. изображены два случая, показывающие, что последовательность приближений может быть как сходящейся, так и расходящейся.
Достаточное условие сходимости.
Теорема. Пусть уравнение  имеет единственный корень на отрезке [a,b] и выполнены условия:
имеет единственный корень на отрезке [a,b] и выполнены условия:
1) функция 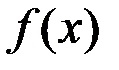 определена и дифференцируема на отрезке [a,b],
определена и дифференцируема на отрезке [a,b],
2) причем все значения 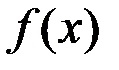 Î[a,b],
Î[a,b],
3) существует такое вещественное q, что 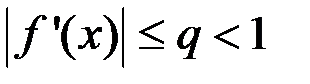 для
для 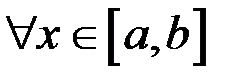 .
.
Тогда процесс итерации  сходится независимо от начального значения
сходится независимо от начального значения  .
.
Доказательство. Рассм. два последовательных приближения  и
и  . Отсюда
. Отсюда  . Применяя теорему Лагранжа, имеем:
. Применяя теорему Лагранжа, имеем:  , где
, где  . На основании условия (3) теоремы, получим:
. На основании условия (3) теоремы, получим:  . Отсюда, при n=1, 2, 3, …, последовательно выводим:
. Отсюда, при n=1, 2, 3, …, последовательно выводим:


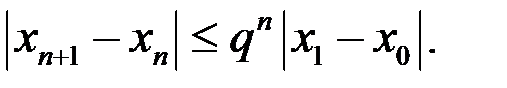 (*)
(*)
Рассмотрим ряд
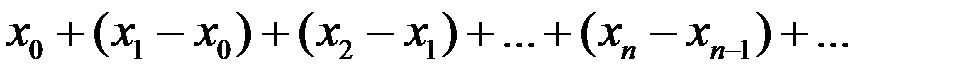 (**)
(**)
Составим частичные суммы этого ряда: 
Заметим, (n+1)-я частичная сумма ряда (**) совпадает с n-м членом итерационной последовательности, т.е. 
|
|
|
Сравним ряд (**) с рядом
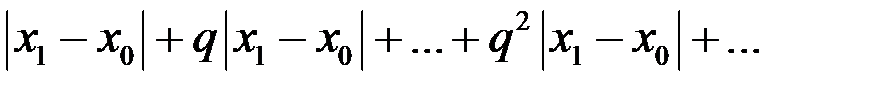 (***)
(***)
В силу неравенств (*) члены ряда (**) по абсолютной величине меньше соответствующих членов геометрической прогрессии (***) со знаменателем q<1, поэтому ряд (**) сходится и притом абсолютно. Следовательно, существует  , причем, очевидно,
, причем, очевидно,  . Переходя к пределу в равенстве
. Переходя к пределу в равенстве 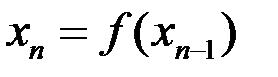 , в силу непрерывности функции
, в силу непрерывности функции  получаем:
получаем:  .
.
Т.о.,  есть корень уравнения
есть корень уравнения  . Что и требовалось доказать.
. Что и требовалось доказать.
Дата добавления: 2018-08-06; просмотров: 798; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
