ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ. ФОРМУЛЫ НЬЮТОНА.
Часто интерполирование ведется для функций, заданных таблицами с равноотстоящими значениями аргумента. В этом случае шаг таблицы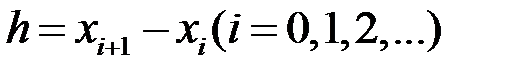 
является величиной постоянной.
Конечные разности.Пусть функция задана таблицей вида табл.1
| 
| 
| 
| ... | 
| 
| |
| F(x) |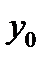 
| 
| 
| 
| 
|
с постоянным шагом. Разности между значениями функции в соседних узлах интерполяции называются конечными разностями первого порядка:
.
Из конечных разностей первого порядка образуются конечные разности второго порядка 
Продолжая этот процесс, можно по заданной таблице функции составить таблицу конечных разностей (табл.2 ).
| 
| 
| 
| ||
| 
| 
| 
| … | |
| 
| 
| |||
| … | |||||
| |||||
| 
| 
| |||
| 
|
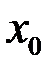
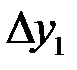
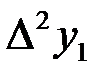
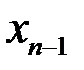
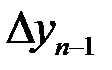
Конечные разности любого порядка могут быть представлены через значения функции.Для разностей первого порядка это следует из определения. Для разностей второго порядка имеем 
.
Аналогично для разностей третьего порядка
Методом, математической индукции можно доказать, что 
(1)
Первая интерполяционная формула Ньютона.
Пусть для функции, заданной таблицей с постоянным шагом, составлена таблица конечных разностей (см. табл. 2). Будем искать интерполяционный многочлен в виде
(2)
Это — многочлен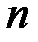 
-й степени. Полагая 
из (2) находим 
, откуда 
. Далее, полагая 
, получаем 
, откуда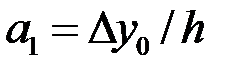 
.При 
, имеем 
т.е 
или 
откуда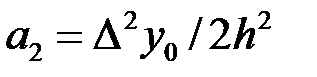 
. => 
.В общем случае выражение для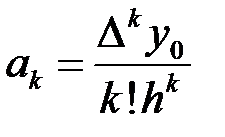 
.(3). Подставим теперь (3) в выражение для многочлена (2)
|
|
|
(4)
Часто эта формула записывается в несколько ином виде. Введем вместо переменной х новую переменную t: 
или 
. Тогда 
и т.д. После этого формула (4) примет вид
(5)
Формула (5) – первой интерполяционной формулой Ньютона.Эта формула применяется для интерполирования в начале отрезка интерполяции, для значений t в интервале (0, 1). Первую интерполяционную формулу Ньютона – формулой для интерполирования вперед.
Вторая интерполяционная формула Ньютона
Когда значение аргумента находится ближе к концу отрезка интерполяции, применять первую интерполяционную формулу становится невыгодно.
В этом случае применяется формула для интерполирования назад — вторая интерполяционная формула Ньютона, которая ищется в виде:
. (6)
Коэффициенты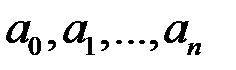 
находятся из условия совпадения значений функции и интерполяционного многочлена в узлах 
.(7).Подставляя (7) в (6) и переходя к переменной 
получим окончательный вид второй интерполяционной формулы Ньютона: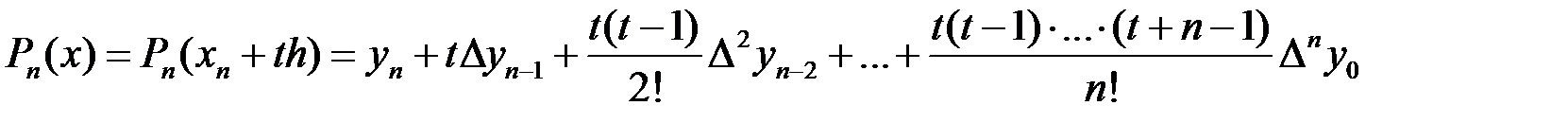 
. (8)
Погрешность многочленной интерполяции.
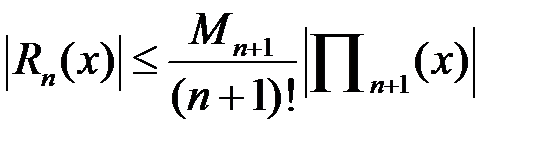(9).Используя подстановки 
и 
и заменяясоответствующим образом выражение для 
, можно получить из (9) формулы оценки погрешностей интерполирования по первой и второй интерполяционным формулам Ньютона
|
|
|
(10) 
(11)
Связь между конечными разностями и точностью интерполирования по формулам Ньютона подтверждается следующими соображениями. Принимая во внимание, что при малых значениях hи при условии непрерывности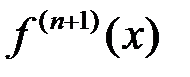 
можно приближенно считать 
где 
. (т.е 
-максимальная из модулей конечных разностей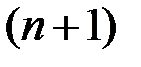 
-го порядка). При этом условии оценки (10) и (11) остаточных членов первой и второй интерполяционных формул Ньютона принимают следующий вид:
. (12)
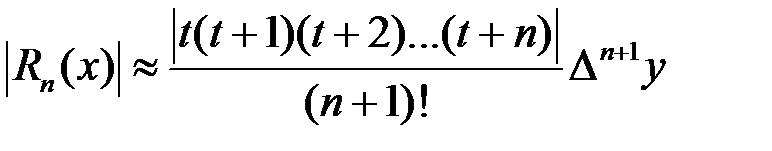. (13)
Дата добавления: 2018-08-06; просмотров: 695; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!