Комбинации геометрических тел. Взаимное расположение двух сфер.
Возможны различные случаи
Пусть R1и R2– радиусы первой и второй окружности соответственно, а d- расстояние между их центрами:
1. ЕслиR1+ R2<d, то сферы не пересекаются (т.е. не имеют общих точек) и расположены одна вне другой.
2. Если R1 +R2 =d , то сферы имеют единственную общую точку (касаются). Касательная плоскость к сфере , проведенная через эту точку, является одновременно касательной плоскостью к сфере . При этом сферы расположены по разные стороны от указанной плоскости (касаются внешним образом).
3. Если | R1 -R2|<d<R1 +R2 , то сферы пересекаются, т.е. имеют более одной общей точки.
4. Если d=| R1 -R2| , то сферы касаются и расположены по одну сторону от общей касательной плоскости (касаются внутренним образом) при R1<>R2 . В случае R1=R2 это одна и та же сфера.
5. Если R1<>R2 и d<| R1 -R2| , то сферы не пересекаются и расположены одна внутри другой. При d=0 их центры --- это одна и та же точка (сферы концентричны).
Комбинации шара с многогранниками. Шар, вписанный в пирамиду.
Шар называется вписанным в пирамиду, если касается всех граней пирамиды.
В пирамиду можно вписать шар т. и т. т. к. выполняется любое из условий:
1) Существует единственная точка равноудаленная от всех граней пирамиды
Центр шара вписанного в многограник лежит в точке пересечения биссектрисных плоскостей всех двугранных углов многограника.
2) Шар можно вписать в любую правильную пирамиду.
|
|
|
Центр шара лежит на высоте пирамиды и совпадает с центром окружности, вписанной в равнобедренный треугольник, боковой стороной которого является апофема (высота боковой грани) пирамиды, а высотой — высота пирамиды.
Радиус шара равен радиусу этой окружности.
Сечение полуплоскостью, проходящей через центр шара и апофему пирамиды. (Полуплоскость ограничена прямой, проходящей через высоту пирамиды.)
Радиус шара R, высота пирамиды Н и радиус окружности r, вписанной в основание пирамиды, связаны соотношением:
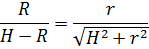
Комбинации шара с многогранниками. Сфера, описанная около пирамиды.
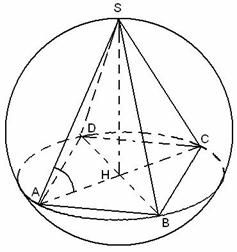Сфера называется описанной около многограника, если все вершины многограника лежат на сфере.
Пирамида вписана в сферу, если все вершины пирамиды лежат на сфере.
Около пирамиды можно описать сферу, т и т т к можно описать окружность вокруг основания пирамиды.Отсюда следует что около любой треугольной пирамиды можно описать сферу, и около любой правильной пирамиды.
Следствие 1. Центр шара, описанного около пирамиды лежит в точке пересечения прямой, перпендикулярной основанию пирамиды, проходящей через центр окружности, описанной около этого основания, и плоскости, перпендикулярной любому боковому ребру, проведенной через сере дину этого ребра.
|
|
|
Следствие 2. Если боковые ребра пирамиды равны между собой (или равно наклонены к плоскости основания), то около такой пирамиды можно описать шар.Центр этого шара в этом случае лежит в точке пересечения высоты пирамиды (или ее продолжения) с осью симметрии бокового ребра, лежащей в плоскости бокового ребра и высоты.
Дата добавления: 2018-05-13; просмотров: 822; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!