Вычисление расстояний в пространстве. Расстояние от точки до прямой. Расстояние от точки до плоскости. Расстояние между скрещивающимися прямыми.
Расстояние от точки до прямой
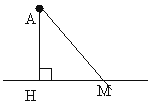Длина перпендикуляра, опущенного из данной точки на прямую, называется расстоянием от дочки до прямой.
Расстояние от точки до плоскости
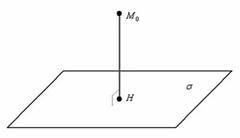Расстояние от точки до плоскости — это наименьшее из расстояний между этой точкой и точками плоскости. Известно, что расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость.
Расстояние между скрещивающимися прямыми.
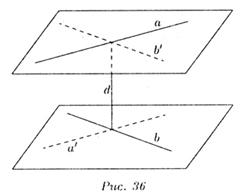Общим перпендикуляром двух скрешивающихся прямых называется отрезок с концами на этих прямых, являющийся перпендикуляром к каждой из них.
Расстояние между скрешивающимися прямыми называется длина их общего перпендикуляра. Оно равно расстоянию между параллельными плоскостями, проходяшими через эти прямые.
Виды многогранников. Призма. Виды призм. Пирамида. Виды пирамид.
Многогранником называется ограниченное тело, поверхность которого состоит из конечного числа многоугольников.
Многоугольники- грани многограника, стороны многоугольников – ребра м, а вершины многоугольников- это вершеины многограника.
Грани имеющие общее ребро называются смежными.
Формула Эйлера: Число вершин-число ребер+число граней=2
Призма
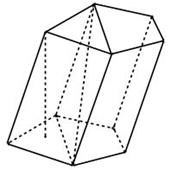Призма-это многограник у которого две грани равные n-угольники(основания) с соответственно паралельными сторонами, а все остальные грани – паралелограммы, у каждого из которых две стороны являются соответственными сторонами оснований.
|
|
|
Свойства призмы
· Основания равны и лежат в параллельных плоскостях.
· Боковые ребра призмы параллельны и равны.
· Боковая поверхность состоит из параллелограммов.
· Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани, называется диагональю призмы.
Призмы бывают 3-ех угольные, 4-ех угольные и т.д., по числу вершин в основании.
Призмы бывают прямыми и наклонными. Призма называется прямой если все боковые грани- прямоугольники.(все боковые ребра перпендикулярны плоскоти основания). Призма не являющейся прямой называется наклонной.
V=Sосн.*h ; Sп.п.=2Sосн.+Sбок.
Пирамида
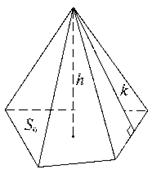Пирамида- многогранник, в основании которого лежит n-угольник,а боковые граникоторого являются треугольниками с общей вершиной, которую называют вершиной пирамиды.
Высота пирамиды-это перпендикуляр опущенный с вершины пирамиды на плоскость основания.
V=1/3 *Sосн.h
Пирамида называется правильной, если ее основание правильный многоугольник. Апофема-высота боковой грани.
Свойства правильной пирамиды:
· боковые ребра правильной пирамиды равны;
· в правильной пирамиде все боковые грани — равные равнобедренные треугольники;
|
|
|
· в любую правильную пирамиду можно как вписать, так и описать около неё сферу;
· если центры вписанной и описанной сферы совпадают, то сумма плоских углов при вершине пирамиды равна π, а каждый из них соответственно π/n, где n — количество сторон многоугольника основания;
· площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Усеченная пирамида-многограник, часть пирамиды заключенная между основанием и секущей плоскостью паралельной плоскости основания.(боковые грани - трапеции)
Vусеч.=1/3 *h(S1+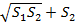 
)
Объем наклонной призмы
V = Sа. где S — площадь перпендикулярного сечения наклонной призмы, a - боковое ребро.
Док-во:
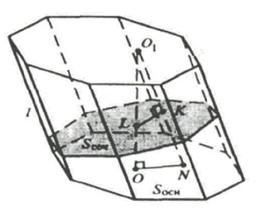Пусть α и β — плоскости оснований призмы. Проведем плоскость γ, перпендикулярно боковым ребрам призмы. Далее, осуществим параллельный перенос фигуры, ограниченной плоскостями β, γ и боковыми ребрами призмы так, чтобы плоскость α совместилась с плоскостью β.
Получим прямую призму, боковая сторона которой равна боковой стороне исходной призмы, а основание является сечением исходной призмы плоскостью, перпендикулярной боковым ребрам.
Объем призмы.
|
|
|
Объем призмы равен произведению площади основания на высоту.
Док-во:
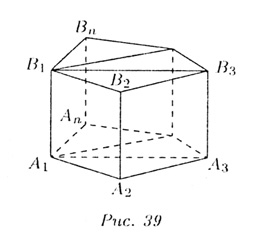Сначала докажем частный случай для произвольной треугольной призмы
Достроим ее до параллелепипеда. Следовательно, параллелепипед состоит из двух равных призм, поэтому
Vпар.=2Vприз.
С другой стороны, Sпар.осн=2Sприз.осн.
а высота призмы и параллелепипеда общая. Из равенства Vпар.=Sосн.h
следует, чтоVприз.= 
Vпар.= Sприз.осн. h
Переходим теперь к общему случаю. Докажем формулу для произвольной n- угольной призмы, высота которой равна h, а площадь основания равна S. Такую призму можно разделить на треугольные призмы высотой h. У нас получаться n-2 треугольных призм. Объем данной призмы равен сумме объемов треугольных призм, состовляющих её.
V=S1h+S2h+…+Sn-2h=(S1+S2+…+Sn-2) h=S h.
Где S1,S2,…,Sn-2–площади треугольников, на которые разбито основание призмы, их сумма равна площади основания призмы.
Объем пирамиды.
Теорема 1
Объем любой треугольной пирамиды равен одной третьей произведения площади её омнования на высоту.
Док-во:
Пусть дана треугольная пирамида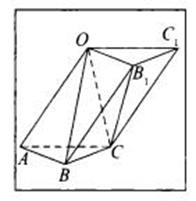 
AOBC, основания треугольник АВС , его площадь равна S, высота проведенная из вершины O равна h. Достроим данную пирамиду до призмы с тем же основанием. Призма сосотоит из трех пирамид – AOBC, OBCB1, OCB1C1.
|
|
|
Рассмотрим пирамиды OBCB1 иOCB1C1, они имеют равные основания BCB1 и CB1C1, а так же общую высоту проведенную из вершины О.По теореме о том что если пирамиды имеют равные высоты и равные площади оснований, то они равны по объему. Следует чтопирамиды OBCB1 и OCB1C1имеют равные объемы. Аналогично пирамиды AOBC и OBCB1имеют равные объемы, так как площади оснований AOBи BOB1равны и они имеют общую высоту из вершины С. Таким образом все три пирамиды имеют равные объемы. Значит объем каждой пирамиды равен трети от объема призмы.
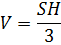
Теорема 2
Объем n-угольной пирамиды равен одной третьей произведения площеди основания на высоту.
Док-во
Разобъем n-угольную пирамиду на n-2 треугольных пирамид, мы знаем что объем трегольной пирамиды равен одной третьей площади её основания на высоту отсюда объем n-угольной пирамиды равен сумме объемов всех пирамид на которые она разбита
V= 
S1h+ S2h+…+ Sn-2h= (S1+S2+…+Sn-2) h= S h.
Где S1,S2,…,Sn-2–площади треугольников, на которые разбито основание n-угольной пирамиды, их сумма равна площади основания.
Объем усеченной пирамиды.
Теорема
Объем усенной пирамиды вычисляется во формуле 
где S1, S2- площади вверхнего и нижнего основания, h– высота усечнной пирамиды.
Док-во:
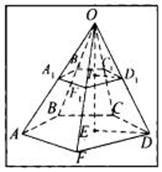Пусть дана усеченная пирамида рассмотрим пирамиду которая дополняеет данную усеченную пирамиду до полной. Тогда объем усеченной пирамиды равен разности объемов полной пирамиды OABCDF идополняющей ОА1В1С1D1F1
Пусть h=TE- высота усеченной пирамиды, TO=x–высота дополняющей пирамиды. Тогда
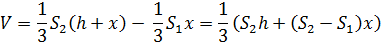
Многоугольники основания усеченной пирамиды подобны значит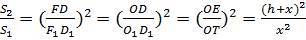 
отсюда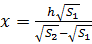 
Подставим в формулу значение х и в результате преобразований получим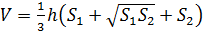 
Дата добавления: 2018-05-13; просмотров: 589; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!