Основные методы решения тригонометрических уравнений
Простейшие тригонометрические уравнения
Основной путь решения тригонометрических уравненийобычно состоит в приведении этого уравнения к алгебраическому уравнению относительно одной тригонометрической функции одного аргумента. При этом широко используются формулы тождественных преобразований тригонометрических функций.
1. Простейшие тригонометрические уравнения (вида f(x) = a).
sin x = a (|a| ≤ 1) ⇒ x = (-1)n arcsin a + πn, n ∈ Z.
cos x = a (|a| ≤ 1) ⇒ x = ± arccos a + 2πn, n ∈ Z.
tg x = a (a ∈ R) ⇒ x = arctg a + πn, n ∈ Z.
ctg x = a (a ∈ R) ⇒ x = arcctg a + πn, n ∈ Z.
Способ замены.
Этот способ следует применять в том случае, когда после преобразований получаем некое алгебраическое уравнения относительно тригонометрической функции.
Уравнение вида a(sin x + cos x) + b sin 2x = c решаем, используя замену sin x + cos x = t. Тогда 1 + sin 2x = t2, а уравнение после замены приобретает видat + b(t2 - 1) = c.
Разложение на множители.
Некоторые уравнения можно преобразовать так, что слева будет произведение, а справа - ноль. После чего необходимо каждый множитель приравнять к нулю и найти всевозможные корни уравнения. (Метод преобразования суммы тригонометрических функций в произведение. После применения формул преобразования суммы в произведение уравнение иногда удается либо разложить на множители, либо существенно упростить.Метод преобразования произведения тригонометрических функций в сумму заключается в применении формул преобразования произведения тригонометрических функций в сумм. После их применения уравнение либо удается либо разложить на множители, либо существенно упростить.)
|
|
|
Однородные тригонометрические уравнения вида
a0(cos x)n + a1(cos x)n - 1sin x + ... + an - 1cos x(sin x)n - 1 + an(sin x)n = 0, n ∈ N, a0 ≠ 0.
Для его решения необходимо поделить уравнение на (sin x)n ≠ 0 (т.к. sin x, cos x одновременно не равны 0). После чего вводим замену ctg x = z и получаем алгебраическое уравнение
a0zn + a1zn - 1 + ... + an - 1z + an = 0, n ∈ N, a0 ≠ 0.
Универсальная замена.
При решении некоторых уравнений (например, asinx + bcosx = c, a, b, c ∈ R) имеет смысл использовать замену tg x/2 = z. После чего sin x = 2z/(1 + z2), cos x = (1 - z2)/(1 + z2), tg x = 2z/(1 - z2). Так как tg x/2 не определен при x = π + 2πn, n ∈ Z, то эта подстановка может привести к потери корней. Потому необходимо проверять, не являются ли числа вида x = π + 2πn, n ∈ Z корнями исходного уравнения.
(Метод подстановки 
, которая часто используется при решении уравнений, содержащих 
и 
. При этом другие тригонометрические функции выражаются через по формулам
, 
, где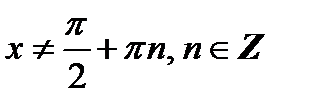 
.
В результате исходное уравнение может быть сведено к рациональному относительно переменной .)
6.Метод понижения степени состоит в использовании формул понижения степени тригонометрических функций с помощью формул 
, 
, 
, .
|
|
|
7.Функциональные методы решения. Если уравнение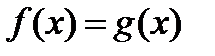 
не удается свести с помощью различных преобразований к уравнению того или иного стандартного вида, для которого известен определенный метод решения, может оказаться полезным использование таких свойств функци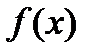й 
и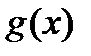 
, как ограниченность, монотонность, четность, периодичность и др.
Дата добавления: 2018-05-13; просмотров: 411; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!