Модуль числа. Решение неравенств, содержащих переменную под знаком модуля
Опр. |f(x)|=f(x), x>0 – модуль функции. –f(x), x<0
а , если а ≥ 0, – модуль числа
Определение:l а l=
–а, если а<0.
Решение неравенств, содержащих переменную под знаком модуля
Способ. Использование геометрического смысла модуля.
Решить неравенство │х–2│< 3
Решение: Решениями неравенства будут числа, находящиеся на расстоянии меньше 3 от нуля модуля, равном 2.
 Ответ: x є (–1;5)
Ответ: x є (–1;5)
когда g(х)а = const, неравенство где эквивалентно следующему:
| 1. | |f(x)| < a | a≤0 | нет решений |
| 2. | |f(x)| < a | a > 0 | -a < f(x) < a |
| 3. | |f(x)| ≤a | a< 0 | нет решений |
| 4. | |f(x)| ≤ a | a = 0 | f(x) = 0 |
| 5. | |f(x)| ≤a | a > 0 | -a ≤ f(x)≤ a |
| 6. | |f(x)| > a | a < 0 | множество решений совпадает с ОДЗ |
| 7. | |f(x)| > a | a = 0 | f(x)≠0 |
| 8. | |f(x)| > a | a > 0 | f(x) < -a или f(x) > a |
| 9. | |f(x)| ≥a | a ≤ 0 | множество решений совпадает с ОДЗ |
| 10.| | f(x)| ≥ a | a > 0 | f(x)≤ -a или f(x)≥ 0 |
Неравенства вида |f(x)| >g(x) (, <, ) рекомендуем решать одним из двух способов, которые рассмотрены ниже.
1). Из определения модуля следует, что изучаемые неравенства равносильны совокупности либо системе следующих неравенств:
|f(x)| > g(х)  ;|f(x)| < g(х)
;|f(x)| < g(х) 
Если неравенства, находящиеся слева от знаков "  ", являются нестрогими, то и в правой части зквивалентностей все неравенства следует заменить соответствующими нестрогими ("направленными" в ту же сторону). В частном случае, когда g{х)а = const, неравенство где эквивалентно следующему:
", являются нестрогими, то и в правой части зквивалентностей все неравенства следует заменить соответствующими нестрогими ("направленными" в ту же сторону). В частном случае, когда g{х)а = const, неравенство где эквивалентно следующему:
2). В ряде случаев (например, если g(х) — квадратный корень либо абсолютная величина, либо любая непрерывная функция, принимающая на всей области определения неотрицательные значения), рассматриваемые неравенства удобнее всего решать возведением в квадрат. Как и в неравенствах |f{x)| > g(х) (≥,≤ 1, <), это можно сделать на множестве g(х) > 0. Для тех х из ОДЗ, где g(х) < 0, неравенство проверяется устно. Далее возможен следующий порядок действий (знак ">" выбран для определенности).
Алгоритм решения неравенства если g(х) > 0
1. Почленно возвести в квадрат |f(x)|2> (g(x))2, используя свойство 6, получим неравенство равносильное данному f(x)2> (g(х))2
2. Перенести (g(х))2 в левую часть f(x)2 - g(x)2> 0
3. Воспользоваться формулой (f(x) - g(х)) (f(x) + g(x)) > 0
4. Применить метод интервалов
Метод интервалов:
Состоит в том, что, зная промежутки, на которых функция, находящая под знаком модуля принимает значения определенных знаков, снимают знак модуля.В общем случае при решении неравенств этим способом поступают так:
а) Находят ОДЗ неравенства.
б) Находят точки в которых функции, стоящие под знаком модуля, равны 0.
в) Полученные точки разделяют ОДЗ на несколько множеств.
г) На каждом, из полученных множеств, определяют знак каждой функци и, согласно определению модуля, снимают знак модуля.
д) Решают каждое из полученных неравенств.
е) Полученные множества объединяют.
5.Уравнения. Равносильные уравнения. Уравнения–следствия.
Теоремы о равносильных преобразованиях уравнений
Уравнение – это равенство содержащее 1 или несколько переменных, которое истинно при одних значениях переменных и ложно при других их значениях.
Решить уравнение – значит найти все значения переменных, при которых это утверждение превращается в верное числовое равенство, или доказать, что таких значений не существует.
Уравнением с одним неизвестным 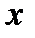 называется равенство
называется равенство 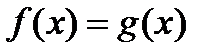 (где
(где  заданные функции), в котором требуется найти все значения
заданные функции), в котором требуется найти все значения 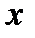 , при которых данное равенство является верным. В частности, может быть
, при которых данное равенство является верным. В частности, может быть  .
.
Корнем (или решением) уравнения называется всякое число 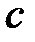 , при подстановке которого в уравнение получается верное числовое равенство
, при подстановке которого в уравнение получается верное числовое равенство 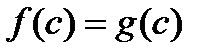 .
.
Замечание. Решение уравнения считается правильным только в том случае, если найдены все корни уравнения и в процессе решения убедительно доказано, что множество корней именно такое, как указанно в ответе. В частности, метод «угадывания» корней считается правильным, если доказано, что других корней нет.
Уравнение вида  , где
, где 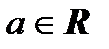 называется уравнением с параметром
называется уравнением с параметром  , если ставиться задача для каждого значения параметра
, если ставиться задача для каждого значения параметра 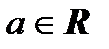 найти множество его корней
найти множество его корней 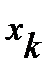 .
.
Процесс решения уравнения – это последовательность некоторых преобразований, производимых над левой и правой частями уравнения и позволяющих заменить данное уравнение другим уравнением, решение которого известно или очевидно.
Пусть в процессе решения уравнения 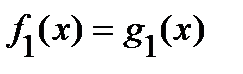 было получено уравнение
было получено уравнение 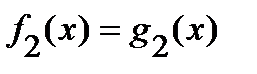 . Говорят, что при этом произошла потеря корней, если существует хотя бы одно число
. Говорят, что при этом произошла потеря корней, если существует хотя бы одно число 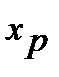 , которое является корнем исходного уравнения, но не является корнем уравнения
, которое является корнем исходного уравнения, но не является корнем уравнения 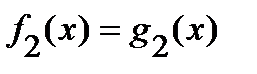 .
.
Если преобразование уравнений может привести к потере корней, необходимо отдельно рассмотреть «выпадающие» в результате выполнения этого преобразования значения переменных, проверив их на принадлежность к множеству решений.
Число  называется посторонним корнемуравнения
называется посторонним корнемуравнения 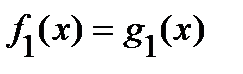 , если оно, являясь корнем уравнения
, если оно, являясь корнем уравнения 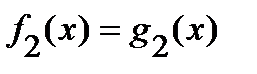 , не является корнем исходного уравнения.
, не является корнем исходного уравнения.
Равносильными называются два уравнения 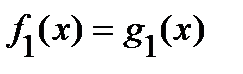 и
и 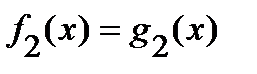 , если они имеют одно и то же множество решений (или оба они не имеют корней).
, если они имеют одно и то же множество решений (или оба они не имеют корней).
Если все корни уравнения 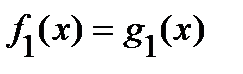 являются корнями уравнения
являются корнями уравнения 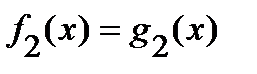 (при этом области определения уравнений могут не совпадать), то второе уравнение называют уравнением–следствием первого и пишут
(при этом области определения уравнений могут не совпадать), то второе уравнение называют уравнением–следствием первого и пишут  .
.
Дата добавления: 2018-05-13; просмотров: 407; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
