Уравнение с параметрами. Решение линейных уравнений с параметрами.
Опр. Если для каждого значения а ∊ А решить уравнение F(x;a)=0 относительно x,то это уравнение наз. уравнение с переменной х и параметром а.(множество А-область значения параметра. Если про множество А ничего не сказано ⇨ а ∊R ,и можно найти все значения a,при переходе через которой произошло качественное изменение - наз. контрольными. Каждое уравнение вида F(x;a)=0 можно рассматривать как уравнение с параметром. Решить уравнение с параметром означает, для каждого допустимого значения параметра найти множество решений уравнения ,или доказать что решений нет.
Линейное уравнение в зависимости от значения параметра а могут иметь: 1) единственное решение 2) бесконечно много решений 3) не иметь решений.
Для того, чтобы решить уравнение с параметром необходимо:
1)определить тип уравнения.
2)привести уравнение к стандартному виду.
3)исследовать решение уравнения, согласно с теорией решения уравнения определенного вида.
Основными методами решения с параметрами является: аналитический , графический (функциональный) и комбинированный.
Cтандартный вид: ax+b=0 (1)
1)когда а≠0,то единственный корень х= 
2)когда 
3)когда 
⇨ решений нет
Пр1. 1+x=ax (аналитический метод)
x-ax=-1
x(1-a)=-1
н.з : a=1 0·x=-1 ·Ø
a 
x 
Ответ : 
при a=1, x
Уравнения с параметрами. Решение квадратных уравнений с параметрами
Опр. Если для каждого значения а ∊ А решить уравнение F(x;a)=0 относительно x,то это уравнение наз. уравнение с переменной х и параметром а.(множество А-область значения параметра. Если про множество А ничего не сказано ⇨ а ∊R ,и можно найти все значения a,при переходе через которой произошло качественное изменение - наз. контрольными. Каждое уравнение вида F(x;a)=0 можно рассматривать как уравнение с параметром. Решить уравнение с параметром означает, для каждого допустимого значения параметра найти множество решений уравнения ,или доказать что решений нет.
|
|
|
Линейное уравнение в зависимости от значения параметра а могут иметь: 1) единственное решение 2) бесконечно много решений 3) не иметь решений.
Для того, чтобы решить уравнение с параметром необходимо:
1)определить тип уравнения.
2)привести уравнение к стандартному виду.
3)исследовать решение уравнения, согласно с теорией решения уравнения определенного вида.
Основными методами решения с параметрами является: аналитический , графический (функциональный) и комбинированный.
Уравнение вида ах2 + bх + с = 0, где х — неизвестное, а, b ,с — выражения, которые зависят лишь от параметров и а ≠ 0, называется квадратным уравнением с параметрами.
Допустимыми будем считать только те значения параметров, при которых а, b и с — действительные числа. В связи с необходимостью выполнения условия а ≠ 0 в квадратных уравнениях приходится разбивать решение на несколько этапов уже на первом шаге.
|
|
|
Пример 1. Решить уравнение (а+1)х2+2ах+а-2=0.
Решение
Поскольку коэффициент при х2(а + 1) может быть как числом, которое не равняется нулю, так и числом, которое равняется нулю, то уже из первого шага нам придется рассмотреть два случая:
а+ 1=0 и а+ 1 ≠ 0.
Если а+ 1=0 (а = –1), то заданное уравнение превращается в уравнение -2х - 3 = 0, которое имеет единый корень х= -3/2.
Если а + 1≠0 (а ≠ –1), то получаем квадратное уравнение, дискриминант которогоD=4(a+2) .
Дальше мы не можем однозначно продолжать решения, так как оно существенным образом зависит от знака дискриминанта. Поэтому приходится рассматривать три случая: D < 0, D = 0, D > 0. Как известно, при D < 0 (а < – 2) квадратное уравнение корней не имеет; при D = 0 (а = – 2) оно имеет два равных корня:x1=x2=-2 ; при D > 0 (а > – 2, но а ≠ – 1) квадратное уравнение имеет два разных корня, которые записываются за общими формулами.
Подадим все эти соображения в виде схемы 1.
Схема 1
Ответ. 1) при а = – 1 ;
2) при а = – 2 х= – 2;
|
|
|
3) при а < -2 корней нет;
4) при – 2 < а<– 1 или при а > – 1 , .
26. Методы решения уравнения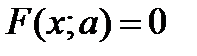 
. Методы решения неравенства 
Каждое уравнение вида f(x;a)=0 можно рассмотреть как уравнение с 2-мя параметрами. Решить такое уравнение – это значит найти такие пары (x;a), которые удовлетворяют данному уравнению. Таким образом уравнение f(x;a)=0 можно рассмотреть как уравнение с 2-мя параметрами (х) и (а). если а – фиксированное значение, то уравнение f(x;a)=0 можно рассматривать как уравнение с одной переменной (х).
Если для каждого значения а из некоторого множества А решить уравнение f(x;a)=0 относительно х, то это уравнение называется уравнением с переменной х и параметром а. множество А – область значения параметра.
Если про множество А ничего не сказано, то а принадлежитR и нужно найти те значения а, при переходе через которые происходят качественные изменения уравнений. Эти значения называются контрольные. Решить уравнение с параметром – значит найти такие контрольные значения, при переходе через которые существенно меняются корни уравнения.
· Аналитический метод решения
· Функциональный и графический (для уравнений и неравенств)
· Полное или комбинированное использование свойств функций и их свойств(для неравенств)
|
|
|
При решении зад с параметрами часто удобно пользоваться графиками входящих в уравнение ф-ий или непосредственно графиком уравнения.
В первом случае мы строим графики в системе хОу а во втором хОа. Особенно удобен такой подход в зад гдг не требуется непосредственно реш ур-ие (или нер-во), а просто надо ответить сколько корней
Пример: для любых значений параметра а опред кол-во корней |x2-2x-3|=a
y= |x2-2x-3|; y=a
Для ответа на вопрос построим в системе координат хОу графики левой и правой частей уравнения…
Дата добавления: 2018-05-13; просмотров: 516; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!