Метод интервалов при решении тригонометрических неравенств
Пример. Решить неравенство  .
.
Решение. Рассмотрим функцию  . Она определена и непрерывна на множестве всех действительных чисел. Функции
. Она определена и непрерывна на множестве всех действительных чисел. Функции  и
и  имеют периоды
имеют периоды 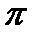 и
и  соответственно. Следовательно, период
соответственно. Следовательно, период  равен
равен  . Найдем нули функции:
. Найдем нули функции:
 ;
; 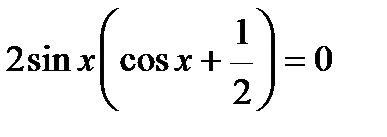 , откуда
, откуда 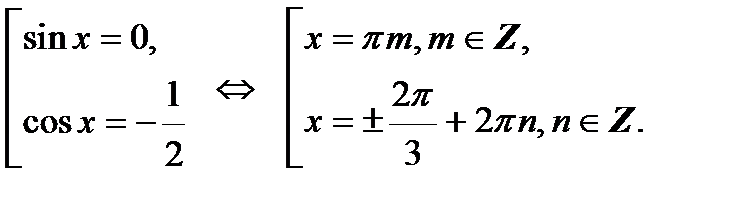
Выберем промежуток  , длина которого равна периоду
, длина которого равна периоду  . Нетрудно заметить, что его концы являются нулями функции (можно было выбрать любой промежуток длины
. Нетрудно заметить, что его концы являются нулями функции (можно было выбрать любой промежуток длины  , но сделанный выбор позволит записать ответ в более компактном виде).
, но сделанный выбор позволит записать ответ в более компактном виде).

|

|

|

|

|

|
Найдем решения исходного неравенства на выбранном интервале. Для этого отметим на промежутке  нули функции и определим знак
нули функции и определим знак  на каждом из получившихся интервалов. Функция
на каждом из получившихся интервалов. Функция  принимает положительные значения на интервалах
принимает положительные значения на интервалах  .
.
Ответ: 
Графики функций и уравнений. Основные преобразования графиков функций
| Общий вид функции | Преобразования |
| y = f(x − a) | Параллельный перенос графика вдоль оси абсцисс (Ох) на | a | единиц вправо, если a > 0; влево, если a < 0. |
| y = f(x) + a | Параллельный перенос графика вдоль оси ординат (Оу) на | a | единиц вверх, если a > 0, вниз, если a < 0. |
| y = f( − x) | Симметричное отражение графика относительно оси ординат. |
| y = − f(x) | Симметричное отражение графика относительно оси абсцисс. |
| y = f(kx) | При k > 1 — сжатие графика к оси ординат в k раз, при 0 < k < 1 — растяжение графика от оси ординат в 1 / k раз. |
| y = kf(x) | При k > 1 — растяжение графика от оси абсцисс в k раз, при 0 < k < 1 — cжатие графика к оси абсцисс в 1 / k раз. |
| y = | f(x) | | При f(x)≥0— график остаётся без изменений, при f(x) < 0 — график симметрично отражается относительно оси абсцисс. |
| y = f( | x | ) | При x≥0 — график остаётся без изменений, при x < 0 — график симметрично отражается относительно оси ординат. |
Пусть даны мн-ва Хи У. Если каждому эл-ту х € Х по опред правилу f поставить в соответствие единственный эл-т у € У то говорят что заданаф-ия у=f(x).Мн-во Х– обл. опр., мн-во У– обл. знач.Задать функцию означает установить правило (закон), с помощью которого по данным значениям независимой переменной следует находить соответствующие им значения функции. Рассмотрим некоторые способы задания функций.
|
|
|
Способы задания ф-ии: 1)Табличный способ; 2)Аналитический (выражено формулой); 3)Графический; 4)Словесный
Основные свойства функций.
Область определения функции и область значений функции.
Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена.Область значений функции - это множество всех действительных значений y, которые принимает функция.
|
|
|
2) Нули функции – такое значение аргумента, при котором значение функции равно нулю.
Пересечение с осями коорд.
4) Монотонность функции.Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
5) Четность (нечетность) функции.
Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат.
Точки экстремума
Периодическость функции.
Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими.
|
|
|
Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.
Другими словами, график функции y = f (х) - это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x).
Дата добавления: 2018-05-13; просмотров: 519; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
