Основные тригонометрические функции и их св-ва
Тригонометрические функции (функции угла) определяются следующими равенствами:
синус: sinα=y, т.е. ордината точки M;
косинус: cosα=x, т.е. абсцисса точки M;
тангенс: tgα=x/y, т. е. отношение ординаты к абсциссе точки M;
котангенс: ctgα=y/x, т. е. отношение абсциссы к ординате точки M.
Функция синус
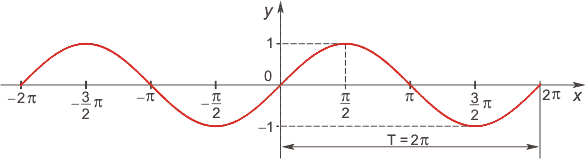
Функция косинус
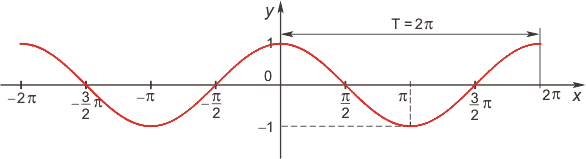
Функция тангенс
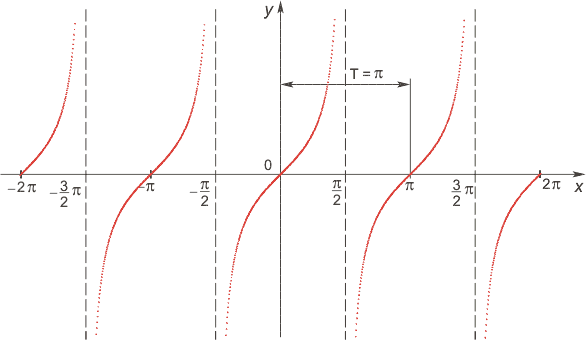
Функция котангенс
Обратные тригонометрические функции, графики, свойства
Функция 
на отрезке 
имеет обратную функцию, которая называется арксинусом
Арксинусомчисла х, где 
называется такое число у,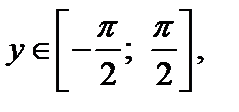 
синус которого равен числу х. Обозначают: 
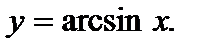Таким образом, 
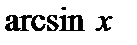– это угол у, измеренный в радианах, такой, что 
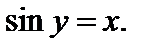Для любого 
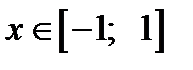имеем 
, 
.
2. Функция 
на отрезке 
имеет обратную функцию, которая называется арккосинусом.
Арккосинусомчисла х, где называется такое число у, 
косинус которого равен числу х. Обозначают: 
Таким образом, 
– это угол у, измеренный в радианах, такой, что 
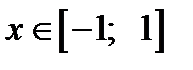Для любого имеем 
, 
.
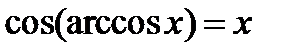3. Функция 
на промежутке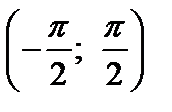 
имеет обратную функцию, которая называется арктангенсом. Арктангенсомчисла х, 
называется такое число у, 
тангенс которого равен числу х. Обозначают: 
Таким образом,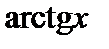 
– это угол у, измеренный в радианах, такой, что 
Для любого 
имеем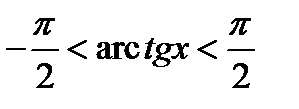 
, 
.
4. Функция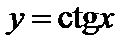 
на промежутке 
имеет обратную функцию, которая называется арккотангенсом. Арккотангенсомчисла х, 
называется число у,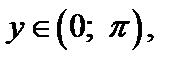 
котангенс которого равен числу х. Обозначается: 
Таким образом, 
– это угол у, измеренный в радианах, такой, что 
Для любого имеем 
, 
.
|
|
|
Функции 
, 
, 
, 
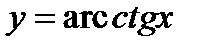называют обратными тригонометрическими функциями или аркфункциями.
Некоторые важные тождества: 
,
,
, 
, 
.
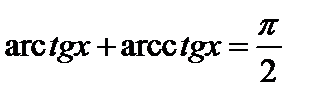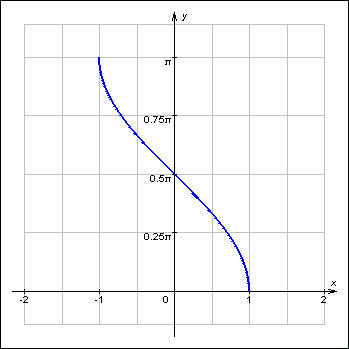
| y = arccos x. |
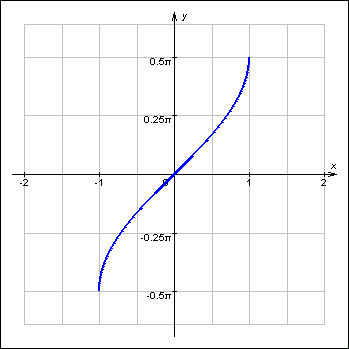
| y = arctg x. |
| y = arcsin x. |
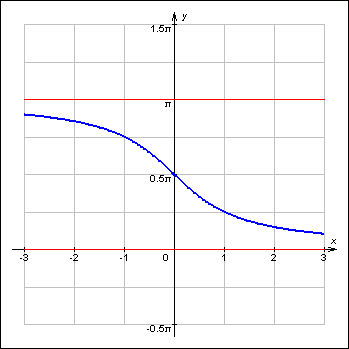
| y = arcctg x. |
При решении уравнений и неравенств смешанного типа приходится применять свойства элементарных функций: область определения, область значений, монотонность, ограниченность, четность и нечетность, периодичность.
Ограниченность множества значений функции
Уравнение f(x)=g(x) равносильно системе уравнений f(x)=A;g(x)=A, если для всех x€X справедливы неравенства f(x)≤A и g(x)≥A.
Монотонность функции
1) Если функция f возрастает (убывает) на множестве X, то уравнение f(x)=A на множестве X имеет не более одного корня.
2) Если функция f возрастает (убывает), а функция g убывает (возрастает) на множестве X, то уравнение f(x)=g(x) на множестве X имеет не более одного корня.
3) Если f(x) - монотонно возрастающая функция, то уравнения f(x)=x и f(f(x))=x равносильны.
Периодичность функции
|
|
|
1) Сумма двух функций с соизмеримыми периодами T1 и T2 является функция с периодом НОД(T1,T2).
2) Сумма двух функций с несоизмеримыми периодами является непериодической функцией.
3) Не существует периодических функций, не равных константе, у которой периодами являются несоизмеримые числа.
Иногда полезно рассмотреть эскизы графиков функци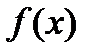й 
и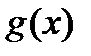 
, входящих в уравнение 
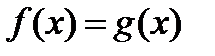. Этот метод, не являющийся строгим решением, может помочь установить:а) существуют ли у данного уравнения корни и сколько их;б) на какие множества следует разбить область определения уравнения, чтобы на каждом из этих множеств использовать свой способ решения.
Использование области опр.
В начале решения уравнения полезно найти область определения уравнения. Если она состоит из нескольких точек, то остается только проверить, какие из них удовлетворяют уравнению. Если область определения – пустое множество, то уравнение не имеет решений. Если же область определения более сложная или ее вычисление связано с трудностями, используется другой метод.
Дата добавления: 2018-05-13; просмотров: 708; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!