Иррациональные неравенства. Основные методы решения иррациональных неравенств
Нер-во – наз иррац если некоторые входящие в него вункции находятся под знаком корня.
Основным методом решения иррационального неравенства является сведение его к системе рациональных неравенств или совокупности таких систем. При этом чаще всего используются следующие равносильности (в нижеследующих формула звездочка у неравенства означает, что данное неравенство заменяется на нестрогое, если исходное неравенство является нестрогим):
1) 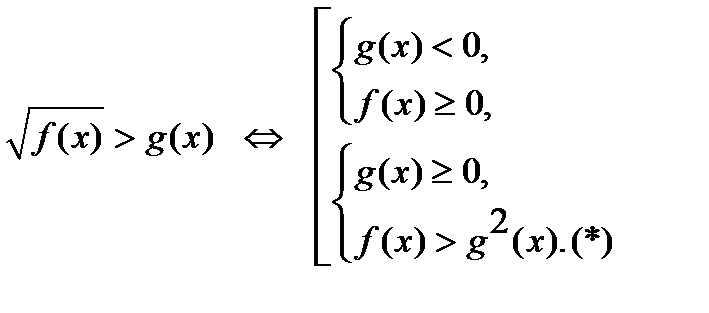 2)
2) 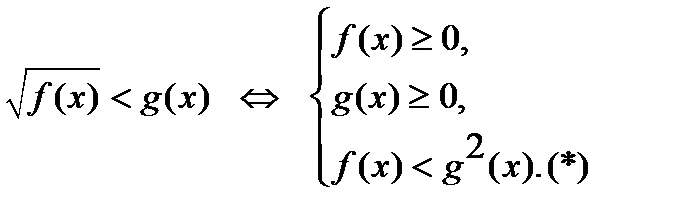
3) 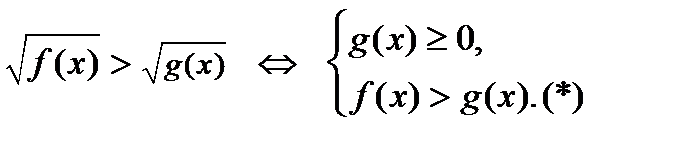 4)
4) 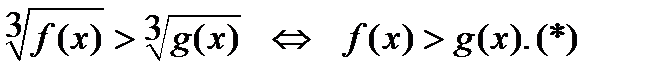
5) 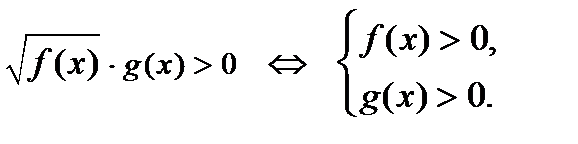 6)
6) 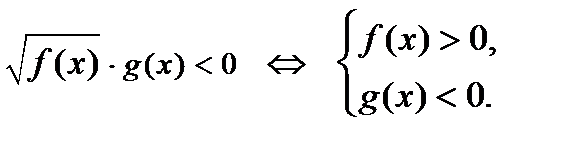
7) 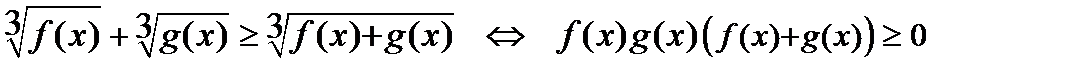 .
.
Замечание. При решении иррациональных неравенств, как правило, приходится возводить обе части неравенства в натуральную степень. В этом случае необходимо следить за тем, чтобы преобразования были равносильными, лишь тогда можно избежать потери или приобретения лишних решений.
Неравенства с тремя квадратными радикалами равносильными преобразованиями сводятся к одному из типов неравенств с единственным радикалом. Например, одна из схем решения неравенства
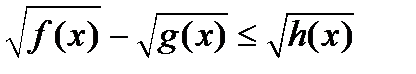 такова. Сначала находим область определения
такова. Сначала находим область определения 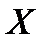 неравенства из системы
неравенства из системы 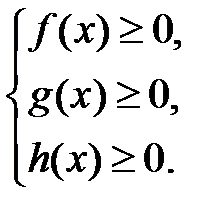 Затем для всех
Затем для всех 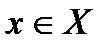 переносом члена с «минусом» в другую часть неравенства обеспечивается неотрицательность обеих частей, которые затем возводятся в квадрат. В результате получается неравенство с одним радикалом:
переносом члена с «минусом» в другую часть неравенства обеспечивается неотрицательность обеих частей, которые затем возводятся в квадрат. В результате получается неравенство с одним радикалом:
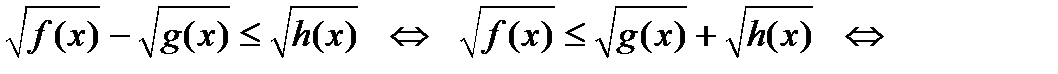
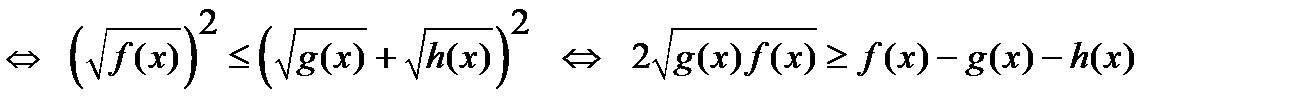 ,
,
которое решается по известной (приведенной выше схеме).
Показательные уравнения. Основные методы решения показательных уравнений
Показательным уравнением называется уравнение, которое содержит неизвестную величину в показателе степени при постоянном основании a (a> 0).
Типы показательных уравнений и способы их решения
Всюду далее f(x), g(x) – некоторые выражения с неизвестной величиной x.
I тип: уравнение вида 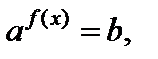 где
где 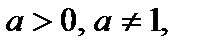 (1) имеет решение, если b > 0. Его решают логарифмированием по основанию a:
(1) имеет решение, если b > 0. Его решают логарифмированием по основанию a: 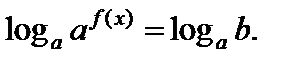 Тогда
Тогда 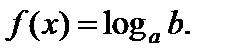 (2)
(2)
Решение уравнения (2) производят соответственно типу этого уравнения.
II тип: уравнение вида 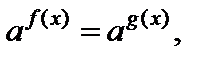 где
где 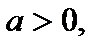 (3) по свойству равенства степеней равносильно уравнению
(3) по свойству равенства степеней равносильно уравнению 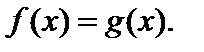 Последнее уравнение решают в зависимости от его типа.
Последнее уравнение решают в зависимости от его типа.
III тип: уравнение вида 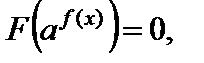 (4) где F – некоторое выражение относительно
(4) где F – некоторое выражение относительно 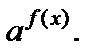
Производят замену переменной 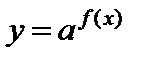 и решают уравнение F(y) = 0. Если
и решают уравнение F(y) = 0. Если 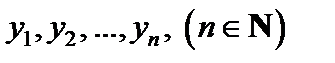 – корни уравнения, то после возвращения к старой переменной решение уравнения (4) сводится к решению равносильной ему совокупности уравнений
– корни уравнения, то после возвращения к старой переменной решение уравнения (4) сводится к решению равносильной ему совокупности уравнений 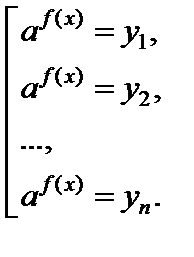
IV тип: уравнения, решаемые графическим методом.
Для таких уравнений строят соответствующие графики для левой и правой частей уравнения. Определяют, для каких значений x графики имеют общую ординату. Используют также иные функциональные свойства, в частности, монотонность функции (возрастание, убывание).
Показательно-степенным уравнением называется уравнение, в котором неизвестная величина содержится и в основании степени, и в показателе. Такие уравнения принято решать при условии, что основания степени положительны (ОДЗ уравнения).
Дата добавления: 2018-05-13; просмотров: 483; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
