Использование ограниченности функций.
Рациональные уравнения и методы их решения
Уравнение – это равенство содержащее 1 или несколько переменных, которое истинно при одних значениях переменных и ложно при других их значениях.
Решить уравнение – значит найти все значения переменных, при которых это утверждение превращается в верное числовое равенство, или доказать, что таких значений не существует.
Уравнением с одним неизвестным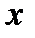 
называется равенство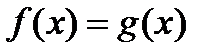 
Областью определения уравнения называется множество всех значений переменной 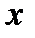, при которых одновременно имеют смысл и левая, и правая части уравнения. Область определения уравнения определяется пересечением областей определения функций 
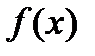и 
.
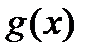Корнем (или решением) уравнения называется всякое число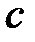 
, при подстановке которого в уравнение получается верное числовое равенство 
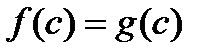. Уравнение может иметь один, два, три и большее число корней, а также бесконечное их множество или не иметь корней вовсе.
Замечание. Решение уравнения считается правильным только в том случае, если найдены все корни уравнения и в процессе решения убедительно доказано, что множество корней именно такое, как указанно в ответе. В частности, метод «угадывания» корней считается правильным, если доказано, что других корней нет.
Уравнение вида P(x) = 0, где P(x) — целая рациональная функция,называется целым рациональным уравнением.
Решение рационального уравнения P (x) / Q (x) = 0, где P (x) и Q (x)— многочлены, сводится к решению уравнения P (x) = 0 ипроверке того, что корни удовлетворяют условию Q (x) не= 0.
При решении рациональных уравнений необходимо помнить следующие сведения из алгебры:
1)х=а – корень многочлена Р(х)=0, то Р(х) делится на (х–а) без остатка
2)пусть все коэффициенты многочлена Р(х) – целые числа и старший коэффициент равен1. Если такой многочлен имеет своим корнем рациональное число, то это число целое.
Рациональные уравнения – целые(все преобразования выполняются на области определения уравнения, поэтому получаются равносильные уравнения и проверку не делают);
–дробно–рациональные(при решении дробно–рациональных уравнений Р(х)/Q(x)=0 выполняется умножение на Q(x), что может привести к появлению посторонних корней, поэтому проверку делать необходимо.
Методы их решения
Использование области определения уравнения.
В начале решения уравнения полезно найти область определения уравнения. Если она состоит из нескольких точек, то остается только проверить, какие из них удовлетворяют уравнению. Если область определения – пустое множество, то уравнение не имеет решений. Если же область определения более сложная или ее вычисление связано с трудностями, используется другой метод.
Разложение на множители.
Если в уравнении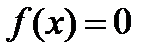 
функцию 
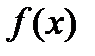можно разложить на множители, т.е. представить ее в виде произведения нескольких других функций, 
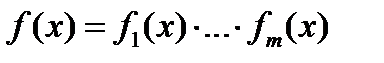, то решение исходного уравнения для 
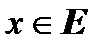сводится к решению совокупности уравнений: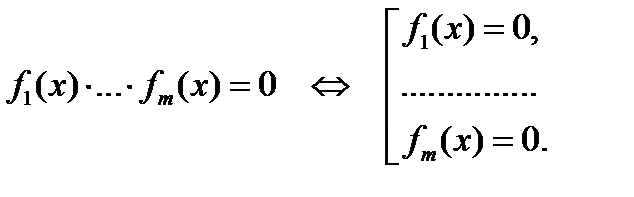 
Замена переменной.
Если уравнение можно представить в виде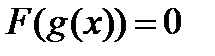 
, то заменой 
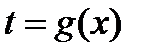решение исходного уравнения сводится к нахождению корней 
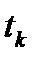уравнения 
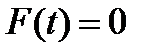и последующему решению уравнения 
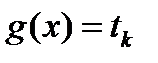для каждого полученного корня.
Функциональные методы
Использование ограниченности функций.
Некоторые уравнения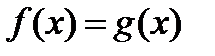 
таковы, что при любом значении 
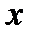из области его определения левая и правая части уравнения удовлетворяют условиям 
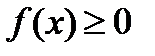и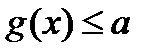 
соответственно, где 
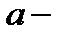некоторое число. Тогда решение уравнения сводится к нахождению значений 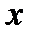, для которых одновременно 
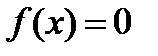и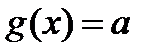 
.
Если же хотя бы одно из неравенств строго, то исходное уравнение не имеет решений.
5. Использование монотонности функций.Если на некотором промежутке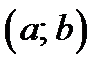 
функци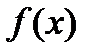и 
и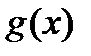 
, входящие в уравнение 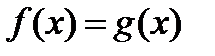таковы, что 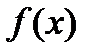непрерывна и возрастает, а 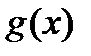непрерывна и убывает, то равенство 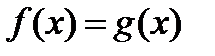возможно только при единственном значении 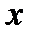, которое и является корнем данного уравнения на рассматриваемом промежутке. Иногда этот корень можно найти подбором.
6. Графический метод. Иногда полезно рассмотреть эскизы графиков функци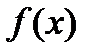й и 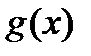, входящих в уравнение 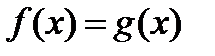. Этот метод, не являющийся строгим решением, может помочь установить:а) существуют ли у данного уравнения корни и сколько их;б) на какие множества следует разбить область определения уравнения, чтобы на каждом из этих множеств использовать свой способ решения.
Дата добавления: 2018-05-13; просмотров: 279; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!