Рациональные неравенства и методы их решения
Пусть f(x)=0 числовая функция одной или нескольких переменных (аргументов). Решить неравенство f(x) < 0 (f(x) > 0) (1) - это значит найти все значения аргумента (аргументов) функции, при которых неравенство (1) справедливо. Множество всех значении аргумента (аргументов) функции, при которых неравенство (1) справедливо, называется множеством решении неравенства или просто решением неравенства.
Два неравенства считаются эквивалентными, если множества их решении совпадают.
Под множеством допустимых значений неизвестных, входящих в неравенство, понимают область определения функции f(x)=0.
Алгебраические неравенства.
Линейными (строгими и нестрогими) называются неравенства вида
ax + b > 0, ax + b < 0 (ax + b>=0, ax + b<=0)
Квадратными (строгими и нестрогими) называются неравенства вида
ax2 + bx + c > 0, ax2 + bx + c < 0,
ax2 + bx + c>= 0, ax2 + bx + c<= 0, где a, b, c – некоторые действительные числа и а ≠ 0.
Квадратное неравенство ax2 + bx + c > 0 в зависимости от значения своих коэффициентов a, b и c имеет решения:
при а > 0 и D = b2 – 4ac ≠0 , то х принадлежит интервалу
при а > 0 и D < 0 x – любое действительное число;
при а < 0 и D ≠0 x(( –х1 ; ;х1 ) );
при а < 0 и D < 0 x = ( (т. е. решении нет ).
Решение неравенства ax2 + bx + c < 0 сводится к решению рассмотренного неравенства, если обе части неравенства умножить на (–1).
Метод интервалов.(основной метод)
Находим область определения функции, затем отмечаем в этой области нули функции, которые разбивают область определения на несколько промежутков, внутри каждого из которых функция определена, непрерывна и сохраняет знак. Для определения знака функции на конкретном промежутке находим знак в любой (удобной) точке этого промежутка.
|
|
|
Дробно–рациональные неравенства.
Решение рационального неравенства Pn(x)/Qn(x) > 0 (5) где Рn(х) и Qm(х) (многочлены, сводится к решению эквивалентного неравенства (4) следующим образом: умножив обе части неравенства (5) на многочлен [Qm(x)]2, который положителен при всех допустимых значениях неизвестного х (т.е. при тех х, при которых Qm(x) ( 0), получим неравенство Рn(х) ( Qm(x) > 0, эквивалентное неравенству (5).
ГРАФИЧЕСКОЕ РЕШЕНИЕ НЕРАВЕНСТВ
Неравенства с одной или двумя переменными можно решать графически.
Неравенство с одной переменой можно записать так: f(x) > g(x), где f(x) и g(x) – выражения, содержащие переменную.
Построим в одной системе координат графики функций y = f(x) и
у = g(x).
Решение неравенства с двумя переменными f(x,y)>0 есть множество точек плоскости, координаты которых удовлетворяют этому неравенству. Рассмотрим на примерах решение некоторых неравенств с двумя переменными.
|
|
|
Модуль числа. Решение уравнений, содержащих переменную под знаком модуля
Геометрический смысл модуля: 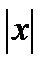 – расстояние от точки 0 до точки
– расстояние от точки 0 до точки 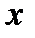 на числовой прямой.Модуль называют еще абсолютной величиной.
на числовой прямой.Модуль называют еще абсолютной величиной.
Аналитически его определяют так: 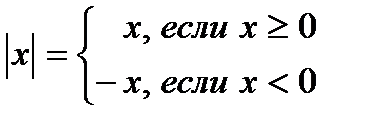 .
.
Если под знаком модуля стоит неотрицательное выражение, то знак модуля можно опустить и выражение, стоящее под знаком модуля, записать без изменения.Если под знаком модуля стоит отрицательное выражение, то знак опустив модуля, выражение, стоящее под знаком модуля, взять в скобки и перед ним поставить знак «минус».
Основные свойства модуля:
1. 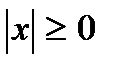 ; 2.
; 2. 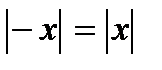 ; 3.
; 3. 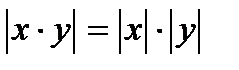 ; 4.
; 4. 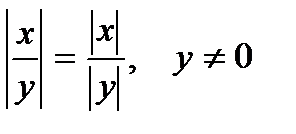 ;
;
5. 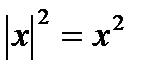 ; 6.
; 6. 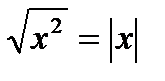 ; 7.
; 7.  ; 8.
; 8. 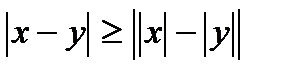 .
.
Используя геометрический смысл модуля и его определение получают способы решения уравнений с модулем.
I тип уравнений
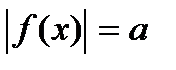 , где
, где 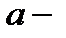 число
число
1) если 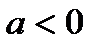 , то решений нет;
, то решений нет;
2) если 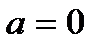 , решаем уравнение
, решаем уравнение 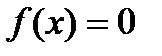 ;
;
3) если 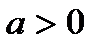 , решаем совокупность уравнений:
, решаем совокупность уравнений: 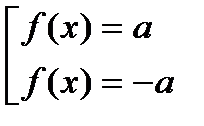 .
.
II тип уравнений
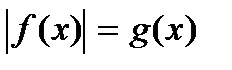 (2), где
(2), где 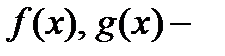 некоторые выражения с переменной.Решать это уравнение можно несколькими способами:
некоторые выражения с переменной.Решать это уравнение можно несколькими способами:
1–й способ – используя определение модуля: 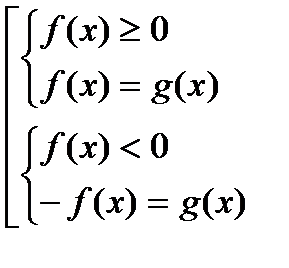
2–й способ – используя подход как к уравнениям Iтипа: 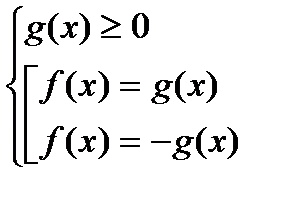
Замечание:1–й и 2–й способ в решении таких уравнений выбирают в зависимости от того, какое неравенство 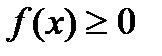 или
или 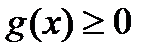 решается легче.
решается легче.
|
|
|
3–й способ – метод интервалов:
1) находим критические точки: 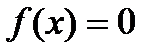 ;
;
2) наносим полученные значения на числовую ось ;
3) определяем знаки  для каждого из полученных интервалов;
для каждого из полученных интервалов;
4) рисуем кривую знаков;
5) решаем уравнение на каждом промежутке в отдельности, раскрывая модуль согласно рисунку;
6) ОДЗ. Если это не вся числовая ось, учитываем сразу на рисунке после того как нарисовали кривую знаков.
III тип уравнений
Уравнения содержат несколько модулей: 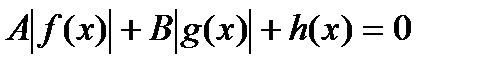 , (3), где
, (3), где 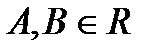 .
.
1–й способ –можно использовать определение модуля и рассматривать 4 случая возможных знаков  ,
, 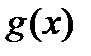 . Этот способ, как правило, не является рациональным.
. Этот способ, как правило, не является рациональным.
2–й способ – метод интервалов: рисуем столько числовых осей и кривых знаков, сколько модулей в уравнении.
IV тип уравнений 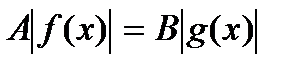 , (4), где
, (4), где 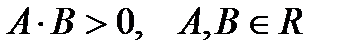 .
.
1–й способ –решаем совокупность уравнений: 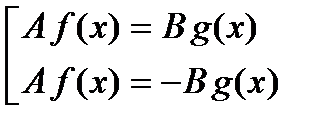 .
.
2–й способ – метод интервалов.
3–й способ –используя теорему равносильности: если обе части уравнения 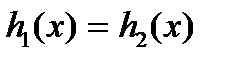 , где
, где 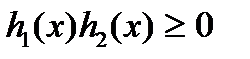 при всех значениях
при всех значениях 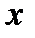 из области определения, возвести в одну и ту же натуральную степень
из области определения, возвести в одну и ту же натуральную степень 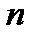 , то получится уравнение
, то получится уравнение 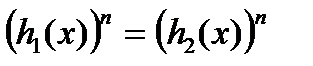 , равносильное данному.Поэтому уравнение (4) равносильно уравнению:
, равносильное данному.Поэтому уравнение (4) равносильно уравнению: 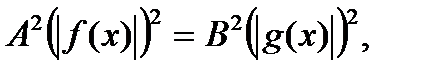 Далее используем свойство квадрата модуля:
Далее используем свойство квадрата модуля: 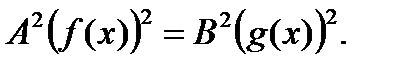
|
|
|
V тип уравненийЭто уравнения, решаемые заменой переменной. Например: 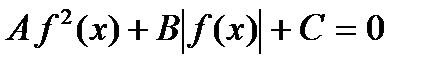 , (5)
, (5)
Дата добавления: 2018-05-13; просмотров: 420; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
