Основные виды четырехугольников, их св-ва и признаки
Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не лежат на одной прямой, а соединяющие их отрезки не пересекаются.
Две несмежные стороны четырехугольника называются противоположными . Две вершины, не являющиеся соседними, называются также противоположными.
Четырехугольники бывают выпуклые (S =d1d2 sinα) иневыпуклые.
Виды четырёхугольников
ПараллелограммS = aha= absinα=d1d2sinα
Параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны.
Свойства параллелограмма
· противолежащие стороны равны;
· противоположные углы равны;
· диагонали точкой пересечения делятся пополам;
· сумма углов, прилежащих к одной стороне, равна 180°;
· сумма квадратов диагоналей равна сумме квадратов всех сторон: d12+d22=2(a2+b2).
Признаки параллелограмма
· Четырехугольник является параллелограммом, если:
· Две его противоположные стороны равны и параллельны.
· Противоположные стороны попарно равны.
· Противоположные углы попарно равны.
· Диагонали точкой пересечения делятся пополам.
ТрапецияS = (a+b)h/2
Трапецией называется четырехугольник, у которого две противолежащие стороны параллельны, а две другие непараллельны.
Параллельные стороны трапеции называются ее основаниями, а непараллельные стороны — боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией.
|
|
|
Трапеция называется равнобедренной (или равнобокой), если ее боковые стороны равны.
Трапеция, один из углов которой прямой, называется прямоугольной.
Свойства трапеции
ее средняя линия параллельна основаниям и равна их полусумме;
если трапеция равнобокая, то ее диагонали равны и углы при основании равны;
если трапеция равнобокая, то около нее можно описать окружность;
если сумма оснований равна сумме боковых сторон, то в нее можно вписать окружность.
Признаки трапеции
Четырехугольник является трапецией, если его параллельные стороны не равны
ПрямоугольникS = ab=d1d2sinα
Прямоугольником называется параллелограмм, у которого все углы прямые.
Свойства прямоугольникавсе свойства параллелограмма;диагонали равны.
Признаки прямоугольника
Параллелограмм является прямоугольником, если:Один из его углов прямой.Его диагонали равны.
РомбS = aha= a2sinα=d1d2
Ромбом называется параллелограмм, у которого все стороны равны.
Свойства ромбавсе свойства параллелограмма;диагонали перпендикулярны;диагонали являются биссектрисами его углов.
Признаки ромба
Параллелограмм является ромбом, если:
|
|
|
Две его смежные стороны равны.
Его диагонали перпендикулярны.
Одна из диагоналей является биссектрисой его угла.
КвадратS = a2=d2
Квадратом называется прямоугольник, у которого все стороны равны.
Свойства квадрата
все углы квадрата прямые;диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
Признаки квадратаПрямоугольник является квадратом, если он обладает каким-нибудь признаком ромба.
Вписанные четырехугольники. Вписанные многоугольники
· Четырёхугольник, все вершины которого лежат на окружности, называется вписанным.
· Сумма противоположных углов вписанного четырёхугольника равна 180°.
· Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон (теорема Птолемея).
· Площадь S вписанного четырёхугольника со сторонами a, b, c, d можно вычислить по формулам: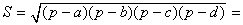 
,где p – полупериметр, R – радиус окружности.
· Если a, b, c, d – длины сторон четырёхугольника,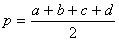 
– его полупериметр, а α – сумма его противоположных углов, то площадь S четырёхугольника равна
.
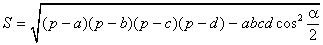В качестве α здесь можно взять сумму любой из двух пар противоположных углов, результат от этого не зависит. В случае четырёхугольника, вписанного в окружность, эта формула принимает более простой вид:
|
|
|
;это равенство и называется формулой Брахмагупты. Если четырёхугольник имеет и описанную и вписанную окружности, то формула становится совсем короткой: 
.
Если четырехугольник вписан в окружность, то сумма его противоположных углов равна 1800 (свойство вписанных четырехугольников).
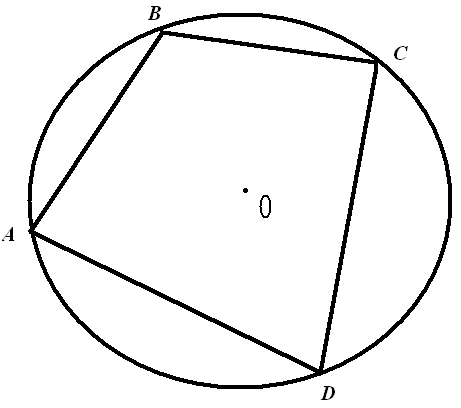1 Действительно, пусть четырехугольник АВСД вписан в окружность (рис.3.61).Тогда сумма его углов А и С измеряется полусуммой дуг ВСП и ВЛП, составляющих полную окружность, а потому равна 180°. И Рассмотрим первый случай. Продолжим тогда сторону ВА за точку А до пересечения с окружностью Р в точке М и проведем хорду МБ (рис.3.63).Четырехугольник ВСБМ вписан в окружность Р. Как доказано, АС+ АМ= 180о. Но АА >АМ (как внешний угол треугольника БМА), а значит АА+АС>180о. Получили противоречие. Следовательно, точка А не может лежать внутри круга, ограниченного окружностью Р.
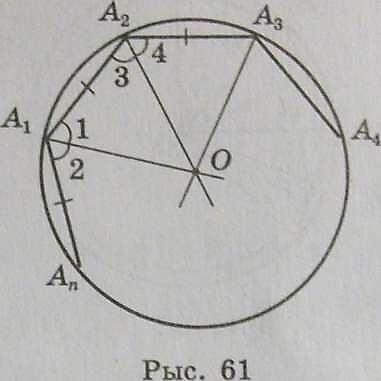Тэарэма (аб акружнасці, апісанай каля правільнага многавугольніка). Каля любога правільнага многавугольніка можна апісаць акружнасць, і прытым толькі адну. Дадзена: А 1 А 2А3 ••• Аn —правільны многавугольнік. Даказаць: існуе пункт, роўнааддалены ад усіх вяршынь. Ён адзіны. Доказ. 1. Дакажам існаван- не. Няхай О — пункт перасячэння бісектрыс вуглоў Аг іА2 (рыс. 61). Злучым пункт О адрэзкамі з астатнімі вяршынямі многаву- гольніка і дакажам, што ОА1= ОА2 = ... = ОАп. 1) ПаколькіÐ А1=Ð А2тоÐ 1 = =Ð 3, значыць, трохвугольнік А1А20 раўнабедраны і ОАг = ОА2. 2) Трохвугольнікі А1А20 і А3А2О роўныя па дзвюх стара- нах і вуглу паміж імі (А1А2 = АзА2, А2О — агульная старана і Ð 3 = Ð 4), значыць, ОА3 = ОАг.
|
|
|
3)Аналагічна можна даказаць, што ОА4 = ОА2, ОА5 = ОА3 і г.д. 4) Такім чынам, ОА1 = ОА2 = ... = ОАт, значыць, пункт О роўнааддалены ад усіх вяршынь многавугольніка. Таму акружнасць со (О, ОА1) з'яўляецца апісанай каля многаву- гольніка.
2. Дакажам адзінкавасць. Для гэтага разгледзім якія-не- будзь тры вяршыні многавугольніка, напрыклад, А1 А2, А3. Паколькі праз гэтыя пункты праходзіць толькі адна акруж- насць, то і каля многавугольніка А1, А2, ... Аnможна апісаць толькі адну акружнасць.
Дата добавления: 2018-05-13; просмотров: 1183; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!