Примеры по выполнению практической работы
Пример 1. Составить для выборки 1, 10, -2, 1,0, 1, 10, 7, -2, 10, 10, 7
вариационный ряд и найти ее размах.
Решение: записав заданную выборку в виде неубывающей последовательности, получим вариационный ряд
-2,-2,0, 1, 1, 1,7,7, 10, 10, 10, 10.
Размах данной выборки равен 10 - (-2) =12.
Пример 2Для выборки 3,8,-1,3, 0, 5,3,-1,3, 5 определить объем и размах. Записать выборку в виде вариационного ряда и в виде статистического ряда. Найти выборочное распределение. Построить полигон частот.
Решение: Объем выборки n = 10, ее размах равен 8 - (-1) = 9. Записав значения выборки в виде неубывающей последовательности получим вариационный ряд
-1,-1,0, 3,3, 3,3, 5, 5, 8.
Статистический ряд можно записать в виде последовательности пар чисел - (-1;2), (0;1), (3;4), 5;2), (8;1) или в виде таблицы
| -1 | 0 | 3 | 5 | 8 |
| 2 | 1 | 4 | 2 | 1 |
Для контроля находим сумму частот: 2+ 1 +4 + 2+ 1 = 10 и убеждаемся в том, что она равна объему выборки.
Вычислив относительные частоты, найдем выборочное распределение:
| -1 | 0 | 3 | 5 | 8 |
| 
| 
| 
| 
|
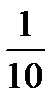
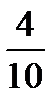
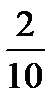
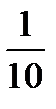
Для контроля убеждаемся в том, что сумма относительных частот равна единице:
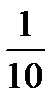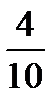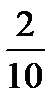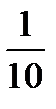+ + + + =1.
Полигон частот для заданной выборки имеет вид:
|
|
|
Пример 3. При измерении напряжения в электросети получена следующая выборка:
218, 221, 215, 225, 225, 217,
224, 220, 220, 219, 221, 219,
222, 227, 218, 220, 223, 230,
223, 216, 224, 227, 220, 222
(данные выражены в вольтах). Построить гистограмму частот, если число частичных промежутков равно 5.
Решение: наименьшее значение выборки равно 215, наибольшее — 230.
Находим длину частичных промежутков 
. Подсчитываем с учетом кратности число значений выборки, попавших в каждый промежуток.
Для первого промежутка [215; 218) это число равно 3, для второго [218; 221) оно равно 8, для третьего [221; 224) — 6, для четвертого [224; 227) — 5, для пятого [227; 230] — 2. Следовательно, высоты прямоугольников (слева направо), образующих гистограмму, равны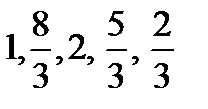 
По полученным данным строим гистограмму
Для контроля убеждаемся в том, что площадь гистограммы равна объему выборки:
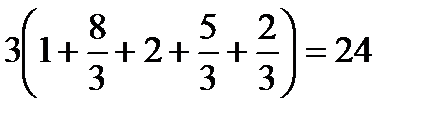
Пример 4. На основании данных о средней заработной плате работников в области в тыс. руб., которые помещены в интервальный вариационный ряд в таблицу, построить гистограмму распределения частот зарплаты работников:
|
|
|
| Заработная плата | 1-3 | 3-5 | 5-7 | 7-9 | 9-11 | 11-13 |
| Число Работников | 12 | 23 | 37 | 19 | 15 | 9 |
Решение: при построении гистограммы по оси абсцисс откладываются значения изучаемого признака (границы интервалов), а по оси у – соответствующие частоты, в том случае, если интервалы одинаковой величины. Используя мастер диаграмм в MS Excel, получим гистограмму:
Гистограмма распределения частот зарплаты работников
Пример 3. Для выборки 4,5,3,2, 1,2,0,7,7,3 найти выборочную среднюю 
, выборочную дисперсию S0, исправленную выборочную дисперсию S.
Решение: объем выборки п = 10. По формуле (5) находим выборочную среднюю:
Чтобы найти выборочную дисперсию, воспользуемся формулой (9). Для этого вычислим среднее квадратов значений выборки:
Теперь по формуле (9) находим S0 = 16,6 -3,42= 5,04. Наконец, используя формулу (10), вычисляем исправленную выборочную дисперсию:
Пример 4. Для выборки 3,8-1,3,0,5,3,4,3,5 найти выборочную среднюю , выборочную дисперсию S0, исправленную выборочную дисперсию S.
Решение: статистический ряд для для данной выборки имеет вид
|
|
|
| -1 | 0 | 3 | 5 | 8 |
| 2 | 1 | 4 | 2 | 1 |
Объем выборки п=10. Выборочную среднюю найдем по формуле (6):
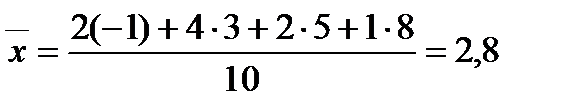
Вычислим среднее квадратов значений выборки:
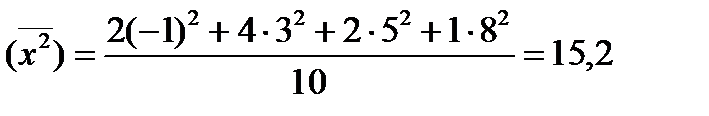
Согласно формуле (9) находим выборочную дисперсию:
S0 = 15,2-2,82= 7,36.
Для вычисления исправленной выборочной дисперсии воспользуемся формулой (10):
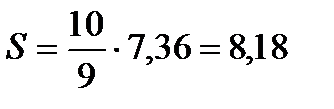
Задания для практического занятия:
Вариант 1
1.Для выборки 1,1,2,-5,4,3,3,8,8,1 определите объем и размах. Запишите выборку в виде вариационного ряда и в виде статистического ряда. Найдите выборочное распределение.
2. Для выборки, заданной статистическим рядом
| 2 | 4 | 6 | 8 |
| 5 | 2 | 1 | 3 |
постройте 1) полигон частот; 2) полигон относительных частот;
3. Для выборки, заданной вариационным рядом -5, -5, 2, 3, 5,10,15, 15, 20, 20, найдите выборочную среднюю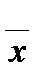 
; выборочную дисперсию S0, несмещенную выборочную дисперсию S.
4. Произведено выборочное обследование коммерческих фирм по затратам на ре
кламу, результаты которого представлены в таблице:
| Затраты на рекламу (усл. ден. ед.) | Кол-во фирм |
| 40-60 | 4 |
| 60-80 | 3 |
| 80-100 | 5 |
| 100-120 | 6 |
| 120-140 | 2 |
По данным выборочного обследования постройте гистограмму частот, используя мастер диаграмм в MS Excel.
|
|
|
Вариант 2
1.Для выборки -3,1,2,4,3,4,4,1,2,1 определите объем и размах. Запишите выборку в виде вариационного ряда и в виде статистического ряда. Найдите выборочное распределение.
2. Для выборки, заданной статистическим рядом
| -1 | 1 | 3 | 7 |
| 1 | 3 | 4 | 2 |
постройте 1) полигон частот; 2) полигон относительных частот
3. Для выборки, заданной статистическим рядом
| -1 | 1 | 3 | 5 | 7 | 9 |
| 2 | 2 | 1 | 3 | 1 | 1 |
найдите выборочную среднюю 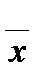; выборочную дисперсию S0, несмещенную
выборочную дисперсию S;
4. В результате выборочного обследования коммерческих банков о размере прибыли за год получено следующее распределение:
| Размер прибыли (млн руб.) | Число банков |
| 10- 20 20-30 30-40 40-50 50-60 | 5 10 20 15 10 |
По данным выборочного обследования постройте гистограмму частот, используя мастер диаграмм в MS Excel.
Вариант 3
1.Для выборки 4,8,8,-4,2, 3,2,7,2,2 определите объем и размах. Запишите выборку в виде вариационного ряда и в виде статистического ряда. Найдите выборочное распределение.
2. Для выборки, заданной статистическим рядом
| 0 | 3 | 7 | 9 |
| 2 | 4 | 1 | 3 |
постройте 1) полигон частот; 2) полигон относительных частот
3. Для выборки, заданной вариационным рядом 2, 4, 4, 4, 5, 5, 5, 5, 10, 10, найдите выборочную среднюю 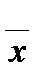; выборочную дисперсию S0, несмещенную выборочную дисперсию S;
4. На заводе проведено выборочное обследование выработки деталей рабочими в день. По результатам наблюдений построили вариационный ряд.
| Количество деталей | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 | 84 |
| Количество рабочих | 2 | 4 | 6 | 8 | 12 | 30 | 18 | 8 | 7 | 5 |
По данным выборочного обследования постройте гистограмму частот, используя мастер диаграмм в MS Excel.
Вариант 4
1.Для выборки 3,4,5,6,7,2,-4,-2,3,6 определите объем и размах. Запишите выборку в виде вариационного ряда и в виде статистического ряда. Найдите выборочное распределение.
2. Для выборки, заданной статистическим рядом
| 5 | 6 | 8 | 10 |
| 4 | 1 | 2 | 3 |
постройте 1) полигон частот; 2) полигон относительных частот;
3. Для выборки, заданной статистическим рядом
| 0 | 2 | 4 | 6 | 8 |
| 1 | 3 | 2 | 1 | 3 |
найдите выборочную среднюю 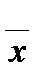; выборочную дисперсию S0, несмещенную
выборочную дисперсию S.
4.Выборочные данные декоративных изделий показали отклонения от стандартного размера, которые помещены в вариационный рад:
| Отклонение | 10,2 | 10,4 | 10,6 | 10,8 | 11 | 11,2 | 11,4 | 11,6 | 11,8 | 12 |
| Количество изделий | 2 | 3 | 8 | 13 | 15 | 20 | 12 | 10 | 6 | 1 |
По данным выборочного обследования постройте гистограмму частот, используя мастер диаграмм в MS Excel.
Контрольные вопросы
1. Что называют: а) генеральной совокупностью; б) выборочной совокупностью; в) объемом выборки?
2. Дайте определение вариационного ряда. Что называют размахом выборки?
3. Как для данной выборки получают статистический ряд и выборочное распределение?
4. Какие графические изображения выборок вы знаете?
5. Чему равна площадь гистограммы относительных частот?
6. Дайте определение выборочных характеристик: а) выборочной средней;
б) выборочной дисперсии;
7. Как связаны между собой выборочная дисперсия и исправленная выборочная дисперсия?
Дата добавления: 2018-05-12; просмотров: 21019; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!