Построение графической диаграммы выборки, расчёт характеристик выборки»

 

Учебная цель:научиться строить графические диаграммы выборки, рассчитывать характеристики выборки

Образовательные результаты, заявленные во ФГОС третьего поколения:

 

Студент должен

уметь:

- вычислять вероятности событий с использованием элементов комбинаторики;

знать:

- основы теории вероятностей и математической статистики;

Краткие теоретические и учебно-методические материалы по теме практической работы

    В самых различных областях производственной и научной деятельности приходится проводить изучение (обследование, измерение, проверку) объектов, принадлежащих некоторой совокупности, по какому-либо признаку. При этом иногда приходится исследовать каждый объект совокупности, т. е. проводить сплошное исследование. Однако на практике гораздо чаще применяется выборочное исследование. При выборочном исследовании из всей совокупности отбирают некоторым образом определенное число объектов и только их подвергают исследованию. При этом совокупность всех исследуемых объектов называют генеральной совокупностью.

Выборкой называют совокупность случайно отобранных объектов из генеральной совокупности. Под случайным отбором при образовании выборки понимают такой отбор, при котором все объекты генеральной совокупности имеют одинаковую вероятность попасть в выборку.

Выборку можно проводить двумя основными способами. При первом способе объект извлекают из генеральной совокупности, исследуют и возвращают в исходную генеральную совокупность; затем снова извлекают некоторый объект, исследуют и возвращают в генеральную совокупность и т. д. Полученную таким образом выборку называют повторной. При втором способе после исследования объекты в генеральную совокупность не возвращают, и выборку в этом случае называют бесповторной.

Число объектов выборочной или генеральной совокупности называют объемом выборки. Например, если из 10 000 изделий для контроля отобрано 100 изделий, то объем генеральной совокупности N=10 000, а объем выборки n=100.

  Для того чтобы по выборке можно было с определенной уверенностью судить о всей генеральной совокупности, выборка должна достаточно полно отражать изучаемое свойство объектов генеральной совокупности,т.е быть репрезентативной. Для этого  необходимо, чтобы отбор объектов в выборку осуществлялся действительно случайно и  чтобы изучаемому свойству была присуща статистическая устойчивость .

Пусть для изучения количественного (дискретного или непрерывного) признака Х из генеральной совокупности извлечена выборка

 

                                                      x_1, х₂, x_{3, …}  x_n ,                   (1)

 

Разность между наибольшим значением числовой выборки и ее наименьшим значением называют размахом выборки.

Наблюдавшиеся значения х_i признака Х называются вариантами, а неубывающую последовательность вариант называют вариационным рядом.  

Пусть при исследовании некоторой генеральной совокупности получена числовая выборка объема n, причем значение х₁ встретилось в выборке n₁ раз, значение х₂ - n₂ раз, ..., значение х_k — n_k раз. Числа n₁ , n₂ , …, n_k называют частотами, а их отношения к объему выборки, т. е. отношения    - относительными частотами соответствующих значений x_1, х₂, x_{3, …} х_k   выборки. Очевидно, что сумма частот равна объему выборки, а сумма относительных частот равна единице, т. е.

               n₁ + n₂ + …+ n_k = n , 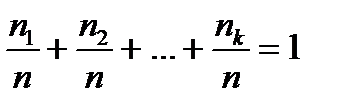                         (2)

 

   Последовательность пар (х₁ ; n₁ ); (х₂ ; n₂ ); ( х₃ ; n₃ ); … (х_k ; n_k )

                      

называют статистическим рядом.  Обычно статистический ряд записывают в виде таблицы:

 

х1	х2	х3	…	xi	…	хk
n1	n2	n3	…	ni	…	nk

(3)
  

Следующей таблицей задается так называемое выборочное распределение, в которой указываются все значения выборки и их соответствующие относительные частоты:

 

х1	х2	х3	…	xi	…	хk
			…		…

(4)

---

Дата добавления: 2018-05-12; просмотров: 1002; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!