Гипергеометрическое распределение

  Можно рассмотреть еще одно распределение, которое называют гипергеометрическим. Пусть имеется множество  элементов, из которых  элементов обладают некоторым признаком 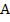. Например, среди 20 шаров, лежащих в урне, 12 шаров имеют красный цвет, тогда если  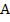—признак того, что шар красный,  =20, а  = 12. Из этого множества извлекают случайным обра­зом без возвращения 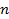 элементов. Требуется найти вероят­ность того, что из них ровно  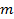элементов обладают призна­ком 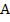. Искомая вероятность (зависящая от 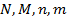) определяется по формуле гипергеометрического распределение:

          (4)

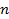где  — общее число вариантов выбора из  элементов по  элементов, т.е. общее число всех единственно возможных, равновозможных и несовместных исходов;   — число исходов, благоприятствующих наступлению интересующего нас события. Следует знать, что если , если . Если по формуле (4) вычислить вероятности для всех возможных значений 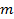, то полученный ряд распределения называется гипергеометрическим законом распределения:

n	0	1	2	…	n
				…

 

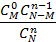
Примеры по выполнению практической работы

 

      Пример 1.Закон распределения вероятностей случайной дискретной величины Х - числа очков, выпадающих при бросании правильной игральной кости, имеет вид, заданный таблицей:

	1	2	3	4	5	6

 

     Пример 2. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте.

Решение: дискретная случайная величина X (число отказавших элементов в одном опыте) имеет следующие возможные значения: x₁ = 0 (ии один из элементов устройства не отказал), х₂ = 1 (отказал один элемент), х₃ = 2 отказали два элемента) и x₄ = 3 (отказали три элемента). Отказы элементов независимы один от другого, вероятности отказа каждого элемента равны между собой, поэтому применима формула Бернулли. Учитывая, что, по условию, n = 3, р = 0,1 (следовательно, q = 1 - 0,1 = 0,9), получим:

Р₃(0) = q³ = 0,9³ = 0,729; P₃(l) = C pq³ = 3 * 0,l * 0,9² = 0,243;

Р₃(2) = С р²q = 3 * 0,1² * 0,9 = 0,027; Р₃(3) = р³ = 0,1³ = 0,001.

Контроль: 0,729 + 0,243 + 0,027 + 0,001 = 1.

Напишем искомый биномиальный закон распределения X:

 

Х	0	1	2	3
Р	0.729	0.243	0.027	0,001

 

       Пример 3. В партии из 10 деталей имеется 8 стандартных. Наудачу отобраны две детали. Составить закон распределения числа стандартных деталей среди отобранных.

Решение:имеем гипергеометрический закон распределения.Случайная величина X - число стандартных деталей среди отобранных деталей — имеет следующие возможные значения: x₁ = 0; x₂ = 1; x₃ = 2. Найдем вероятности возможных значений X по формуле (4)

(N - число деталей в партии, n - число стандартных деталей в партии, m - число отобранных деталей, k - число стандартных деталей среди отобранных), находим:

Р(Х = 0) = ;  Р(Х = 1) =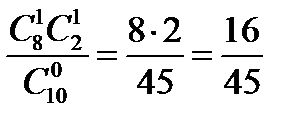

Р(Х = 2) =

Составим искомый закон распределения

 

x	0	1	2
p	1/45	16/45	28/45

 

Контроль: 1/45 + 16/45 + 28/45 = 1.

 

  Пример 4. Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути равна 0,002. Найти вероятности того, что в пути будет повреждено изделий:

а) ровно три; б) менее трех; в) более трех; г) хотя бы одно.

Решение: число n = 500 велико, вероятность р = 0,002 мала и рассматриваемые события (повреждение изделий) независимы, поэтому имеет место формула Пуассона

P_n(k) =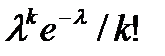

а) Найдем λ = nр = 500 * 0,002 = 1. Найдем вероятность того, что будет повреждено ровно 3 (k = 3) изделия:  Р₅₀₀(3) = e^-1/3! = 0,36788/6 = 0,0613.

б) Найдем вероятность того, что будет повреждено менее трех изделий:

Р₅₀₀(0) + Р₅₀₀(1) + Р₅₀₀(2) = е^-1 + e^-1 + e^-1/2 = (5/2)e^-1 = (5/2) * 0,36788 = 0,9197.

в) Найдем вероятность Р того, что будет повреждено более трех изделий. События «повреждено более трех изделий» и «повреждено не более трех изделий» (обозначим вероятность этого события через Q) - противоположны, поэтому P + Q = l. Отсюда P = 1 - Q = 1 - [Р₅₀₀(0) + Р₅₀₀(1) + Р₅₀₀(2) + Р₅₀₀(3)]

Используя результаты, полученные выше, имеем  P = 1 - [0,9197+0,0613] = =0,019.

г) Найдем вероятность Р₁ того, что будет повреждено хотя бы одно изделие. События «повреждено хотя бы одно изделие» и «ни одно из изделий не повреждено» (обозначим вероятность этого события через Q₁) -противоположные, следовательно, P₁ + Q₁ = l. Отсюда искомая вероятность того, что будет повреждено хотя бы одно изделие, равна

Р₁ = 1 – Q₁ = 1 – P₅₀₀(0) = 1 – e^-1 = 1 - 0,368 = 0,632.

Задания для практического занятия:

Вариант 1

      1. Дискретная случайная величина Х распределена по закону:

Х	3	4	5	6	7
р	р1	0,15	р3	0,25	0,35

Найти вероятности р₁=р(Х=3) и р₃=р(Х=5), если известно, что р₃ в 4 раза больше р_1.

      2. Дан закон распределения случайной величины Х. Найти: а и соответствующий закон распределения.

	1	2	3	4	5
		0,5а²	0,5а	0,2а	0,3а

 

 

      3.Выпущено 500 лотерейных билетов, причём 40 билетов принесут их владельцам выигрыш по 100 рублей, 10 билетов - по 500 рублей, 5 билетов - по 1000 рублей, остальные билеты - безвыигрышные. Найти закон распределения выигрыша для владельца одного билета.

     4.Составить закон распределения числа попаданий в цель при трёх выстрелах, если вероятность попадания при одном выстреле равна 0,85

     5. В партии из 12 деталей имеется 8 стандартных. Наудачу извлекается 4 детали. Составить закон распределения ДСВ Х – числа нестандартных деталей среди отобранных.

     6. Устройство состоит из 1000 элементов, работающих независимо друг от друга Вероятность отказа любого элемента в течение времени Т равна 0,002. Найти вероятность того, что время Т откажет: а) ровно 3 элемента; б) более 4-х элементов.

Вариант 2

     1. Дискретная случайная величина Х распределена по закону:

Х	1	2	3	4	5
р	0,1	р2	0,2	0,3	р5

Найти вероятности р₂=р(Х=2) и р₅=р(Х=5), если известно, что р₂ в 3 раза больше р_5.

         

    2. Дан закон распределения случайной величины Х. Найти: а и соответствующий закон распределения.

	1	2	3	4	5
	а²	2а	а	а²	0,5а

      3.Выпущено 400 лотерейных билетов, причём 25 билетов принесут их владельцам выигрыш 200 рублей, 20 билетов 500 рублей, 15 билетов по 1000 рублей, остальные билеты безвыигрышные. Составить закон распределения выигрыша для владельца одного билета.

      4. Составить закон распределения числа попаданий в цель при трёх выстрелах, если вероятность попадания при одном выстреле равна 0,92

      5. В партии из 15 деталей имеется 4 нестандартных. Наудачу извлекается 3 детали. Составить закон распределения ДСВ Х – числа стандартных деталей среди отобранных.

      6. Учебник издан тиражом 10000 экземпляров. . Вероятность того, что учебник сброшюрован неправильно, равна 0, 0003. Найти вероятность того, что тираж содержит: а) ровно 5 бракованных книг; б) хотя бы одну бракованную книгу.

 

Вариант 3

      1.Дискретная случайная величина Х распределена по закону:

Х	-1	0	1	2	3
р	0,2	р2	р3	0,4	0,1

Найти вероятности р₂=р(Х=0) и р₃=р(Х=1), если известно, что р₂ меньше р₃ на 0,06.

     2. Дан закон распределения случайной величины Х. Найти: а и соответствующий закон распределения.

	1	2	3	4	5
	а²	0,5а	2а²	0,5а	а

          

     3. Выпущено 500 лотерейных билетов, причём 20 из них принесут их владельцам выигрыш 100 рублей, 15 билетов 500 рублей, 10 билетов по 1000 рублей. Составить закон распределения выигрыша для владельца одного билета.

      4. Составить закон распределения числа попаданий в цель при трёх выстрелах, если вероятность попадания при одном выстреле равна 0,87

      5. После ответа студента на экзамене преподаватель задает ему дополнительные вопросы. Преподаватель не задает следующий дополнительный вопрос, если студент отвечает на поставленный вопрос правильно. Максимальное количество дополнительных вопросов – три. Вероятность того, что студент ответит на дополнительный вопрос, равна 0,9. Составить закон распределения ДСВ Х – количество заданных студенту дополнительных вопросов.

      6. Станок- автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной равна 0, 01. Найти вероятность того, сто среди 200 деталей окажется: а) ровно 4 бракованных, б) более двух бракованных.

 

Вариант 4

      1. Дискретная случайная величина Х распределена по закону:

Х	2	4	6	8	10
р	р1	0,2	0,3	р4	0,1

Найти вероятность событий р₁=р(Х=2) и р₄=р(Х=8), если р₄ больше р₁ на 0,08.

 

      2. Дан закон распределения случайной величины Х. Найти а и соответствующий закон распределения.

	1	2	3	4	5
	1,5а²	0,7 а	1,5а²	0,6а	0,7а

 

       3. Куплено 700 лотерейных билетов, причем на каждый из 70 билетов выпал выигрыш в 50 рублей , 50 билетов-100руб.; 10 билетов-500руб, 5 билетов – 700 руб. Составить закон распределения выигрыша для владельца одного билета.

      4. Составить закон распределения числа попаданий в цель при четырех выстрелах, если вероятность попадания при одном выстреле равна 0,81

      5. Телеканал НТВ оценивает вероятность того, что телезритель увидит новую развлекательную программу в 0,2. В случайном порядке выбрано 5 телезрителей. Составить закон распределения числа лиц, видевших эту развлекательную программу.

     6. Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Найти вероятность того, что магазин получит разбитых бутылок: а) ровно две; б) менее трех.

 

 

Контрольные вопросы

     1. Что называется случайной величиной? Какая случайная величина называется дискретной?

     2. Как составить закон распределения случайной величины?

     3. Для каких дискретных случайных величин вероятности появления событий можно вычислять по формуле Бернулли?

     4. Вероятности каких событий определяются по формуле Бернулли? Приведите примеры.

     5. Как определить, что из 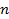 испытаний событие наступит менее (не менее) чем  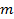раз?

     6. Какая функция называется кривой вероятностей? Выде­лите основные свойства кривой вероятностей.

     7. Сформулируйте локальную теорему Муавра-Лапласа в схеме Бернулли.

     8. Когда формула Муавра- Лапласа дает хорошее прибли­жение для определения вероятности ?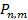

     9. Какое распределение дискретной случайной величины называется распределением Пуассона?

    10. Для каких дискретных случайных величин вероятности появления событий можно вычислять по формуле Пуас­сона?

    11. Какое распределение дискретной случайной величины называется гипергеометрическим распределением?

    12. Для каких дискретных случайных величин вероятности появления событий можно вычислять как гипергеомет­рические?

 

 

Практическая работа № 8

---

Дата добавления: 2018-05-12; просмотров: 1146; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!