Решение задач на вычисление характеристик ДСВ»

Учебная цель: научиться вычислять числовые характеристики дискретной случайной величины

Образовательные результаты, заявленные во ФГОС третьего поколения:

 

Студент должен

уметь:

- вычислять вероятности событий с использованием элементов комбинаторики;

знать:

- основы теории вероятностей и математической статистики;

Краткие теоретические и учебно-методические материалы по теме практической работы

       Если X— случайная величина,  — постоянная, тогда произведение — это новая случайная величина, которая принимает значения, равные произведению значе­ний  на постоянную величину k, с теми же ве­роятностями, что и случайная величина X. Закон распреде­ления случайной величины  имеет вид:

 

			…
			…

 

 

 

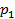
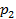
       Квадрат случайной величины X есть новая случайная величина — , которая принимает значения, равные квад­ратам , с теми же вероятностями, что и случай­ная величина X. Закон распределения случайной величины Х²  , имеет вид:

			…
			…

 

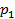
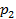
       Пусть имеются две случайные величины  при­нимает значения  с вероятностями 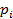 а случайная величина — значения  с вероятностями . Сумма случайных величин  — это новая случайная величина, которая принимает все значения вида  с вероятностями , выражающими вероятность того, что случайная величина X примет значе­ние 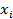 a —значение то есть

                      (1)

Если случайные величины X и У независимы, то:

                          (2)

Закон распределения случайной величины  имеет вид:

			…
			…

 

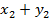
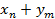
      Разность случайных величин — это новая случай­ная величина, которая принимает все значения вида  а произведение — все значения вида  с вероятнос­тями, определяемыми по формуле (2), если случайные ве­личины  зависимы, и по формуле (3), если они неза­висимы.

      Выполняя указанные математические операции над случай­ными величинами, можно строить другие случайные вели­чины и задавать их соответствующим рядом распределения.

 

Числовые характеристики дискретной случайной величины

       Закон распределения дискретной случайной величины пол­ностью ее характеризует. Однако часто закон распределе­ния неизвестен, и приходится ограничиваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают случайную величину суммарно; такие числа называют числовыми характеристиками случайной величины. К числу важных числовых характеристик отно­сятся математическое ожидание, дисперсия и среднее квадратическое отклонение.

       Математическим ожиданием дискрет­ной случайной величиныназывают сумму произведений всех ее возможных значений на их вероятности. Оно оп­ределяет среднее ожидаемое значение дискретной случай­ной величины.

       Если дискретная случайная величина X задана рядом распределения и принимает значения с соответ­ствующими вероятностями , то математическое ожидание вычисляется по формуле:

                            .                                                 (3)

        Математическое ожидание дискретной случайной вели­чины обладает свойствами, которые вытекают из его опре­деления.

       1. Математическое ожидание постоянной величины С есть постоянная величина

                                                             (4)

      2. Математическое ожидание дискретной случайной ве­личины X, умноженной на постоянную величину С, равно произведению математического ожидания М(Х) на С. То есть постоянный множитель можно выносить за знак суммиро­вания

                                                                           (5)

       3. Математическое ожидание суммы дискретных случайных величин X и У равно сумме их математических ожиданий.

                                                                   (6)

       4. Математическое ожидание произведения независимых дискретных случайных величин X и Y равно произведению их математических ожиданий

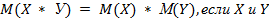 независимы                            (7)

          Иногда математическое ожидание плохо характеризует случайную величину. Это происходит в тех случаях, когда значения случайной величины значительно отклоняются от среднего ожидаемого. Для того чтобы оценить, как рассея­ны возможные значения случайной величины вокруг ее математического ожидания, пользуются числовой характе­ристикой, которую называют дисперсией.

      Дисперсией дискретной случайной ве­личины называют математическое ожидание квадрата от­клонения случайной величины от ее математического ожи­дания:

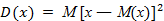                                                     (8)   

  Для вычисления дисперсии иногда бывает удобно пользо­ваться следующей формулой:

              (9)

 

---

Дата добавления: 2018-05-12; просмотров: 1076; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!