Расчеты на прочность при сдвиге
Условие прочности детали конструкции заключается в том, что наибольшее напряжение возникающее в ней (рабочее напряжение) не должно превышать допускаемое.
Расчетная формула при сдвиге

читается следующим образом: касательное напряжение при сдвиге, вычисленное по формуле 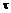 = Q/A, не должно превышать допускаемое.
= Q/A, не должно превышать допускаемое.
207
По этой расчетной формуле проводят проектный и проверочный расчеты и определяют допускаемую нагрузку.
Деформация сдвига, доведенная до разрушения материала, называется срезом (применительно к металлическим деталям) или скалыванием (применительно к неметаллическим конструкциям).
Допускаемое напряжение на срез выбирают для пластичных материалов в зависимости от предела текучести. В машиностроении для штифтов, болтов, шпонок и т. п. принимают
|
|
Для древесины допускаемые напряжения на скалывание во врубках колеблются в пределах от 0,5 до 1,4 МПа и зависят от сорта дерева и направления врубки по отношению к направлению волокон.
При расчетах на срез в случае, если соединение осуществляется несколькими одинаковыми деталями (болтами, заклепками и т. д.), полагают, что все они нагружены одинаково.
Расчеты соединений на срез обычно сопровождают проверкой прочности этих соединений на смятие.
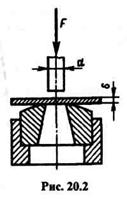
Пример 20.1. Определить силу F, необходимую для пробивания квадратного отверстия размером а = 25 мм в стальной полосе толщиной 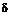 = 10 мм, если предел прочности при срезе
= 10 мм, если предел прочности при срезе 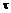 в= 360 МПа. Определить напряжения сжатия в пуансоне (рис. 20.2).
в= 360 МПа. Определить напряжения сжатия в пуансоне (рис. 20.2).
Решение. Определим разрушающую нагрузку F:

Площадь среза Aср равна площади боковой поверхности пробитого отверстия

Следовательно, F =  в Aср= 360
в Aср= 360  106
106  1000
1000  10-6 = 360
10-6 = 360  103 Н. Определим напряжения сжатия в пуансоне:
103 Н. Определим напряжения сжатия в пуансоне:
 с=F/A,
с=F/A,
где А — площадь поперечного сечения пуансона;
А = а2 = 252 -10-6= 625  10-6 м2
10-6 м2
следовательно,
 с = F/A = 360
с = F/A = 360  103/(625
103/(625  10-6) = 576
10-6) = 576  106 Па = 576 МПа.
106 Па = 576 МПа.
Пример 20.2. Определить напряжения смятия и среза в головке стержня, растягиваемого силой F= 100 кН. Дано: D= 32 мм, d= 20 мм, h = 12 мм (рис. 20.3).
Решение. Определим площадь смятия Асми площадь среза Аср головки. Площадь опорной поверхности головки, работающей на смятие, равна

208
|
|
|
|
Площадь среза равна площади боковой поверхности цилиндра диаметром d и высотой h:

Определим напряжения смятия и среза головки:
|
|
Пример 20.3. В условиях примера 19.6 определить напряжения среза в болте (см. рис. 19.13,б).
Решение. Напряжения среза в болте вычисляем по формуле  = F/Aср.
= F/Aср.
Площадь среза Aср представляет собой две площади поперечного сечения болта:
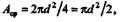
следовательно,
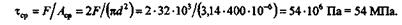
Деформация и закон Гука при сдвиге
Для установления параметров, характеризующих деформацию при сдвиге, рассмотрим элемент бруса в виде параллелепипеда abсd,на грани которого действуют только касательные напряжения 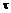 , а противоположную грань параллелепипеда представим жестко защемленной (рис. 20.4). Деформация сдвига в указанном элементе заключается в перекашивании прямых углов параллелепипеда за счет поступательного перемещения грани bс по отношению к сечению, принятому за неподвижное. Деформация сдвига характеризуется углом
, а противоположную грань параллелепипеда представим жестко защемленной (рис. 20.4). Деформация сдвига в указанном элементе заключается в перекашивании прямых углов параллелепипеда за счет поступательного перемещения грани bс по отношению к сечению, принятому за неподвижное. Деформация сдвига характеризуется углом  и называется углом сдвига или относительным сдвигом (так как этот параметр не зависит от
и называется углом сдвига или относительным сдвигом (так как этот параметр не зависит от
209
|
|
расстояния h,на котором происходит сдвиг). Величина bb1, на которую смещается подвижная грань относительно неподвижной, называется абсолютным сдвигом. Относительный сдвиг 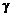 выражается в радианах.
выражается в радианах.
Напряжения и деформации при сдвиге связаны между собой зависимостью, которая называется законом Гука при сдвиге.
Закон Гука при сдвиге справедлив лишь в определенных пределах нагружения и формулируется так: касательное напряжение прямо пропорционально относительному сдвигу.
Математически закон Гука можно записать в виде равенства

Коэффициент пропорциональности G характеризует жесткость материала (т. е. способность сопротивляться упругим деформациям) при сдвиге и называется м о д у л е м сдвига или модулем упругости второго рода.
Модуль упругости и напряжение выражаются в одинаковых единицах:
|
|
Значения G, МПа, для некоторых материалов:
Чугун........................................................ 4,5  104
104
Сталь........................................................ 8,1  104
104
Медь................................. ………………....(4,0...4,9)  104
104
Латунь..................................................... (3,5...3,7)  104
104
Алюминий .................................................. (2,6...2,7)  104
104
Дерево...................................................... 0,055  104
104
В заключение отметим, что между тремя упругими постоянными Е, G и v существует следующая зависимость:

Принимая для сталей v 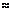 0,25, получаем
0,25, получаем
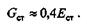
Дата добавления: 2018-04-15; просмотров: 2581; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!