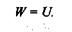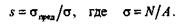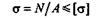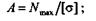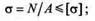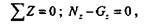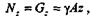Потенциальная энергия деформации

При растяжении

При статическом растяжении образца растягивающая сила F,медленно возрастающая от нуля до какого-то значения, удлиняет образец на величину l и при этом совершает работу W. Эта работа аккумулируется в деформируемом образце в виде потенциальной энергии деформации U,причем, пренебрегая незначительными потерями энергии (например, тепловыми), можно считать, что

Если диаграмма растяжения построена в координатах (F, l), то, как известно из теоретической механики, площадь диаграммы выражает работу деформации. До предела пропорциональности работа выражается площадью треугольника OAK (см. рис 19.6). Таким образом, потенциальная энергия упругой деформации стержня длиной l постоянного поперечного сечения А при одинаковой во всех сечениях продольной силе N = F будет равна

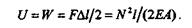
Полная работа, затрачиваемая на разрушение образца, выражается площадью фигуры OABDN диаграммы растяжения, площадь треугольника NDE соответствует работе упругой деформации, исчезающей при разрыве образца.

Удельной потенциальной энергией деформации называется работа деформации, приходящаяся на единицу объема бруса:

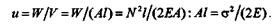
При одновременном действии нескольких растягивающих или сжимающих сил и при ступенчатом изменении размеров поперечного сечения брус разбивают на отдельные участки, отличающиеся значением напряжения; потенциальную энергию деформации всего бруса определяют как сумму потенциальных энергий отдельных участков:

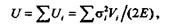
где 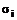— нормальные напряжения в поперечных сечениях на каждом участке;

V_i —объем каждого участка бруса.

Потенциальная энергия деформации выражается в единицах работы — джоулях (Дж), удельная потенциальная энергия — в джоулях на кубический метр (Дж/м³).

Анализируя формулы потенциальной энергии деформации, можно сделать следующие выводы:

1. Потенциальная энергия деформации — величина всегда положительная, так как в ее выражения входят квадраты напряжений или продольных сил.

2. По этой причине при вычислении потенциальной энергии деформации нельзя применять принцип независимости действия сил (из математики известно, что квадрат суммы не равен сумме квадратов слагаемых).

197

Расчеты на прочность

При растяжении и сжатии

В результате проведения механических испытаний устанавливают предельные напряжения, при которых происходит нарушение работы или разрушение деталей конструкции.

Предельным напряжением при статической нагрузке для пластичных материалов является предел текучести, для хрупких — предел прочности. Для обеспечения прочности деталей необходимо, чтобы возникающие в них в процессе эксплуатации напряжения были меньше предельных.

Отношение предельного напряжения к напряжению, возникающему в процессе работы детали, называют коэффициентом запаса прочности и обозначают буквой s:

Очевидно, что недостаточный коэффициент запаса прочности не обеспечит надежности конструкции, а чрезмерный запас прочности приведет к перерасходу материала и утяжелению конструкции. Сечение, для которого коэффициент запаса прочности наименьший, называется опасным.

Минимально необходимый коэффициент запаса прочности называют допускаемым и обозначают [s], Допускаемый коэффициент запаса прочности зависит от свойств, качества и однородности материала, точности представления о нагрузках, действующих на конструкцию, ответственности конструкции и многих других причин. Для пластичных материалов [s]= 1,2... 2,5, для хрупких [s]= 2...5, для древесины [s]= 8...12.

Отношение предельного напряжения к допускаемому коэффициенту запаса прочности называют допускаемым напряжением и обозначают [ ]:

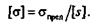
Условие прочности детали конструкции заключается в том, что наибольшее возникающее в ней напряжение (рабочее) не должно превышать I допускаемого:

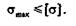
Условие прочности можно записать в ином виде:

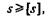
т. е. расчетный коэффициент запаса прочности не должен быть меньше допускаемого.

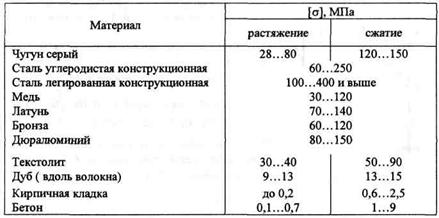
Ориентировочные значения допускаемых напряжений на растяжение и сжатие для некоторых материалов приведены в табл. 19.1.

198

Таблица 19.1

Если допускаемые напряжения при растяжении и сжатии различны, то их обозначают соответственно [ _р] и [ _с].

Расчетная формула при растяжении и сжатии имеет вид

и читается следующим образом: нормальное напряжение в опасном сечении, вычисленное по формуле = N/A, не должно превышать

допускаемое.

При расчете конструкций на прочность встречаются три вида задач, различающихся формой использования расчетной формулы:

1) проектный расчет, при котором определяются размеры опасного сечения по формуле

2) проверочный расчет, при котором определяется рабочее напряжение и сравнивается с допускаемым по формуле

3) определение допускаемой нагрузки ведется по формуле

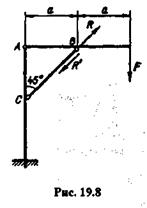
Пример 19.4.Пренебрегая массой конструкции, определить размер дубового подкоса ВС квадратного сечения (рис. 19.8). Крепления в точках А, В и С считать идеально гладкими шарнирами. Дано: F=10 кН, а = 1 м, [ ] =12 МПа.

Решение. Рассмотрим равновесие бруса АВ.Из теоретической механики известно, что реакция прямолинейного стержня, закрепленного двумя концами в

199

идеально гладких шарнирах направлена вдоль стержня. Таким образом, реакция R подкоса ВС направлена вдоль его оси. Подкос работает на сжатие.

Составим уравнение моментов относительно точки A:

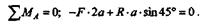
Отсюда, сокращая равенство на а,получаем

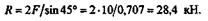
Далее воспользуемся расчетным уравнением при сжатии и определим площадь А поперечного сечения подкоса ВС: = R/A 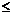[ ], отсюда

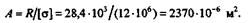
Так как подкос ВС имеет квадратное сечение, то А = b², следовательно,

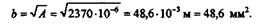
Округлив, принимаем b = 50 мм.

Растяжение под действием

Собственного веса

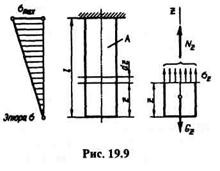
Если ось бруса вертикальна, то собственный вес вызывает деформацию растяжения или сжатия. Рассмотрим брус постоянного сечения весом G, длиной l, закрепленный верхним концом и нагруженный только собственным весом G (рис. 19.9).

Для определения напряжений в поперечном сечении на переменном расстоянии z от нижнего конца применим метод сечений. Рассмотрим равновесие нижней части бруса и составим уравнение равновесия:

откуда

где — удельный вес материала бруса; А — площадь его поперечного сечения.

Напряжение

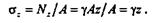
Нормальные напряжения в поперечных сечениях бруса по-200

стоянного сечения, растягиваемого лишь собственным весом, прямо пропорциональны расстоянию сечения от нижнего конца и не зависят от площади сечения.

Очевидно, что опасное сечение бруса будет находиться в заделке:

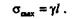
Эпюра распределения нормальных напряжений вдоль оси бруса представляет собой треугольник (см. рис. 19.9).

Определим длину бруса постоянного сечения, при которой напряжение только от собственного веса достигает допускаемого и брус не может нести полезной нагрузки. Такая длина бруса называется предельной:

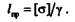
Если _шах станет равным пределу прочности, то брус разрушится от собственного веса. Длина бруса, при которой он разрушается под действием собственного веса, называется критической:

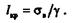
Как видно из формул, предельная и критическая длины не зависят от площади поперечного сечения бруса.

Вычислим для примера критическую длину бруса из стали Ст2, у которой _в= 360 МПа, а удельная сила тяжести = 7,85 10⁴ Н/м²:

Определим удлинение l бруса под действием собственного веса, для чего выделим бесконечно малый элемент длиной dz. Ввиду малости длины элемента будем считать, что в его пределах продольная сила N_z не изменяется. Применив закон Гука, получим

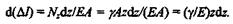
Проинтегрировав это выражение в пределах от 0 до l, получим

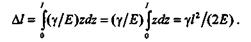
Так как

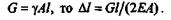
Удлинение бруса постоянного сечения под действием собственного веса в 2 раза меньше удлинения при растяжении силой, равной собственному весу и приложенной к концу бруса.

201

Дата добавления: 2018-04-15; просмотров: 563; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 44 45 46 47 484950 51 52 53 Следующая ⇒

Мы поможем в написании ваших работ!