Закон парности касательных напряжений

Закон парности касательных напряжений форму­лируется так: касательные напряжения в двух взаимно перпендикулярных площадках, перпендикулярные их общему ребру, равны по модулю.

210

Внутри тела вблизи некоторой точки вырежем элементарный парал­лелепипед с размерами dx, dy, dz (рис. 20.5, а).

Пусть на верхней грани этого параллелепипеда действует касатель­ное напряжение т. Сила, действующая в этой грани, равна

Так как параллелепипед находится внутри тела в равновесии, то , следовательно, на нижней грани параллелепипеда будет дейст­вовать такая же сила dQ, но направленная в противоположную сторону. Пара сил (dQ, dQ) будет стремиться вращать параллелепипед против ча­совой стрелки (рис. 20.5, б).

Так как параллелепипед находится в равновесии, то , сле­довательно, пара (dQ, dQ) будет уравновешиваться какой-то другой парой с моментом, равным моменту первой пары. Естественно считать, что вто­рая пара образуется касательными напряжениями 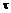', действующими на боковых (правой и левой) гранях параллелепипеда, причем dQ' = 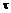'dydz. Следовательно,

или

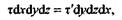
откуда

Обратим внимание на то, что парные касательные напряжения в двух взаимно перпендикулярных сечениях направлены либо к линии пересече­ния плоскостей сечений, либо от этой линии.

211

Напряжения в наклонных сечениях

При растяжении. Главные напряжения

Через всякую точку деформиро­ванного тела можно провести бес­численное множество различно ори­ентированных секущих плоскостей.

Рассмотрим прямой брус по­стоянного поперечного сечения А,растягиваемый силами F (рис. 20.6, а).Рассечем брус плоскостью 1—1, проходящей через точку В и составляющей с поперечным сече­нием угол , отбросим верхнюю часть и рассмотрим равновесие нижней.

Очевидно, что равнодействующая N внутренних сил, действующих в наклонном сечении, будет равна растягивающей силе F:

 

а напряжения  будут параллельны оси бруса (рис.20.6, б). Полагая, что напряжения  распределены по наклонному сечению равномерно, получим

где —площадь наклонного сечения.

Нормальные напряжения в поперечном сечении будут равны

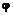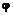Так как  = A/cos , то / = N / = N / (A/cos )= cos .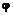

Разложим полное напряжение  в точке наклонного сечения на нор­мальное 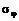и касательное  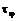напряжения (рис. 20.6, в); тогда

Отсюда следует вывод: при растяжении бруса в наклонных сечениях возникают равномерно распределенные по сечению нормальные и каса­тельные напряжения, и соответствующие этим напряжениям дефор­мации растяжения и сдвига.

Рассмотрим частные случаи:

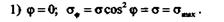
Нормальные напряжения имеют максимальное значение в по­перечном сечении:

Касательные напряжения в поперечном сечении равны нулю;

Каса-

 

тельные напряжения достигают своего максимального значения в сечени­ях, наклоненных к оси под углом 45°. Эти напряжения являются причи­ной появления на растягиваемом образце при достижении предела теку­чести сетки наклонных линий Людерса — Чернова;

В продольных сечениях бруса нет ни касательных, ни нормальных напряжений (вспомним гипотезу о ненадавливании волокон).

Из сказанного следует, что, говоря о напряжении в данной точке, всегда необходимо указать положение секущей плоскости, в которой это напряжение возникает.

Совокупность нормальных и касательных напряжений, возникающих в бесчисленном множестве различно ориентированных площадок, прохо­дящих через данную точку, характеризует напряженное состояние в дан­ной точке.

Площадки, в которых касательные напряжения равны нулю, назы­ваются главными площадками, а возникающие в них нормаль­ные напряжения — главными напряжениями. Как доказывается в теории упругости, в общем случае напряженного состояния в зоне ис­следуемой точки могут существовать три взаимно перпендикулярные главные площадки. В зависимости от количества таких площадок (где 0) различают три основных вида напряженного состояния: линей­ное (одноосное), плоское (двухосное) и объемное (трехосное) (рис. 20.7).

В дальнейшем нас будут интересовать только первые два вида на­пряженного состояния.

213

 

Очевидно, что в рассмотрен­ном случае одноосного растяже­ния главные площадки располо­жены в поперечном и продольном сечениях, т. е. взаимно перпенди­кулярны. Обратим внимание так­же на то, что главные напряжения в данной точке имеют максималь­ное и минимальное значения:

    

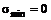
(не будем доказывать, что по­следнее утверждение справедливо и при ).

В дальнейшем нам понадобится зависимость между не равными ну­лю главными напряжениями в двух взаимно перпендикулярных площад­ках (случай плоского напряженного состояния) и максимальными каса­тельными напряжениями в наклонной (по отношению к главным) пло­щадке.

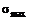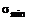Для вывода указанной зависимости внутри бруса вблизи некоторой точки вырежем бесконечно малую призму аbс (рис. 20.8), у которой аb и ас— главные площадки, а и —главные напряжения. Площадь грани bc обозначим dA.

Рассмотрим равновесие призмы, для чего спроецируем действующие на ее гранях силы на ось х:

 

Отсюда

Из этого уравнения следует, что при = 45°

Если 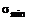=0, то  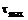= 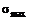/2.

Если в случае плоского напряженного состояния в окрестности данной точки можно выделить элементарный параллелепипед таким образом, чтобы на его гранях действовали только равные между со­бой касательные напряжения (см. рис. 20.5, а),то такой вид напря­женного состояния называется чистым сдвигом. В дальнейшем с чистым сдвигом мы встретимся при изучении теории кручения круглого цилиндра.

214

Глава 21

---

Дата добавления: 2018-04-15; просмотров: 876; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!