Понятие о кручении круглого цилиндра
Кручением называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только крутящий момент.
Деформации кручения возникают, если к прямому брусу в плоскостях, перпендикулярных оси, приложить пары сил. Моменты этих пар будем называть вращающими или скручивающими. Вращающий момент обозначается Т.
Так как на кручение работают валы, обычно имеющие круглое или кольцевое сечение, то рассмотрим кручение круглого цилиндра (рис. 22.1).
Изготовим из резины (для большей наглядности) прямой круговой цилиндрический брус и жестко защемим один его конец; нанесем на его
|
|
поверхности сетку линий, состоящую из образующих и окружностей, а затем приложим к свободному концу бруса пару сил, действующую в плоскости, перпендикулярной оси, т. е. подвергнем брус деформации кручения. При этом:
1) ось цилиндра, называе
мая осью кручения, оста
нется прямолинейной;
2) диаметры окружностей,
нанесенных на поверхности ци
линдра до деформации, при де-
222
формации останутся такими же и расстояние между окружностями не изменится;
3) образующие цилиндра обратятся в винтовые линии.
Из этого можно заключить, что при кручении круглого цилиндра справедлива гипотеза плоских сечений, а также предположить, что радиусы окружностей остаются при деформации прямыми. Так как в поперечных сечениях бруса нет продольных сил, то расстояния между сечениями не изменяются.
|
|
|
Из сказанного выше следует, что деформация кручения круглого цилиндра заключается в повороте поперечных сечений относительно друг друга вокруг оси кручения, причем углы поворота их прямо пропорциональны расстояниям от закрепленного сечения. Угол поворота сечения равен углу закручивания части цилиндра, заключенной между данным сечением и заделкой. Угол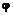 
поворота концевого сечения называется полным углом закручивания цилиндра.
Относительным углом закручивания 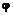0 называется отношение угла закручивания 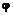z к расстоянию z от данного сечения до заделки. Если брус длиной l имеет постоянное сечение и нагружен скручивающим моментом на конце (т. е. состоит из одного участка), то
Рассматривая тонкий слой материала на поверхности бруса, ограниченный любой ячейкой сетки (например, ячейкой kncd на рис. 22.1), видим, что эта ячейка при деформации перекашивается, принимая положение knc1d1Аналогичную картину мы наблюдали при изучении деформации сдвига.
На этом основании заключаем, что при кручении также возникает деформация сдвига, но не за счет поступательного, а в результате вращательного движения одного поперечного сечения относительно другого. Следовательно, при кручении в поперечных сечениях возникают только касательные внутренние силы, образующие крутящий момент.
|
|
|
Крутящий момент есть результирующий момент относительно оси бруса внутренних касательных сил, действующих в поперечном сечении.
Эпюры крутящих моментов
Для наглядного изображения распределения крутящих моментов вдоль оси бруса строят эпюры крутящих моментов.
Крутящий момент в сечениях бруса определяется с помощью метода сечений. Так как равномерно вращающийся вал, как и неподвижный брус, находится в равновесии, то очевидно, что внутренние силы, возникающие в поперечном сечении, должны уравновешивать внешние моменты, дей-
223
ствующие на рассматриваемую часть бруса. Отсюда следует, что крутящий момент в любом поперечном сечении численно равен алгебраической сумме внешних моментов, приложенных к брусу справа или слева от сечения.
Эпюры крутящих моментов дают возможность определить опасное сечение. В частности, если брус имеет постоянное поперечное сечение, то опасными будут сечения на участке, где возникает наибольший крутящий момент.
Крутящий момент полагаем положительным, если при взгляде со стороны сечения результирующий момент внешних пар, приложенных к рассматриваемой части бруса, будет направлен против часовой стрелки, и наоборот.
|
|
|
Пользуясь принципом смягченных граничных условий, будем полагать, что в поперечном сечении, где приложен вращающий момент, значения крутящего момента меняются скачкообразно.
Пример 22.1.Для трансмиссионного вала (силовую передачу иногда называют трансмиссией), представленного на рис. 22.2, построить эпюры крутящих моментов. Вращающие моменты на шкивах равны: Т1= 600 Н 
м, Т2= 180 Н м, T3 = 300 Н м, Т4=120 Н м. Индексом 1 обозначен ведущий шкив передачи.
Решение. Данный трансмиссионный вал состоит из пяти участков. Пользуясь методом сечений, определим внутренние силовые факторы на участках —
|
|
крутящие моменты Мк. На первом и пятом участках крутящие моменты равны нулю, так как на этих участках вращающие моменты не приложены.
На втором участке
Мк2= Т1 = 600 Н м;
на третьем участке
Мк3= Т1 – Т2=
= 600 - 180 = 420 Н м;
на четвертом участке
Мк4= Т1 – Т2 – Т3 =
= 600-180-300= 120 Н м.
Строим эпюру крутящих моментов, как показано на рис.22.2, а.
Заметим, что «скачок» на эпюре крутящих моментов всегда численно равен значению вращающего мо-
224
мента, приложенного в рассматриваемом сечении.
|
|
|
Из эпюры видно, что наибольший крутящий момент будет на втором участке:
Н м
Рациональным размещением шкивов можно добиться уменьшения значения 
. На рис.22.2, б изображена другая схема расположения шкивов и соответствующая эпюра 
, из которой видно, что значение крутящего момента 
Н м, т.е. в два раза меньше, чем в первом случае. Такое расположение шкивов позволяет передавать заданные мощности с помощью вала меньшего диаметра.
Дата добавления: 2018-04-15; просмотров: 999; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!