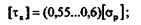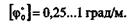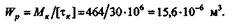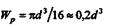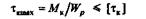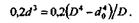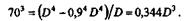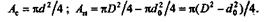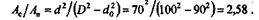Расчеты на прочность и жесткость при кручении

⇐ ПредыдущаяСтр 58 из 72Следующая ⇒

Условие прочности бруса при кручении заключается в том, что наибольшее возникающее в нем касательное напряжение не должно превышать допускаемое. Расчетная фо рмула на прочность при кручении имеет вид 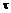= M_к/W_p [ 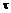_к] и читается так: касательное напряжение в опасном сечении, вычисленное по формуле 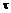= M_к/W_p, не должно превышать допускаемое.

Допускаемое напряжение при кручении выбирают в зависимости от допускаемого напряжения при растяжении, а именно:

для сталей

длячугунов

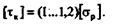
228

Кроме прочности к валам предъявляется требование жесткости, заключающееся в том, что угол закручивания 1 м длины вала не должен превышать определенной величины во избежание, например, пружинения валов или потери точности ходовых винтов токарно-винторезных станков.

Допускаемый угол закручивания 1 м длины вала задается в градусах и обозначается [ 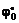]; расчетная формула на жесткость при кручении имеет вид

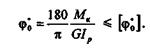
Величины допускаемых углов закручивания зависят от назначения вала; их обычно принимают в следующих пределах:

С помощью полученных расчетных формул выполняют три вида расчетов конструкций на прочность и жесткость при кручении — проектный, проверочный и определение допускаемой нагрузки.

Пример 22.3. Определить диаметр стального вала, передающего мощность Р = 48 кВт при частоте вращения n= 980 об/мин, если допускаемое напряжение кручения [ 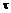_к] = 30МПа.

Решение. Расчетное уравнение на прочность при кручении круглого цилиндра имеет вид:

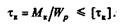
Определим угловую скорость вала:

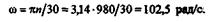
Найдем крутящий момент

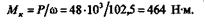
Определим момент сопротивления кручению

Находим требуемый диаметр вала из формулы

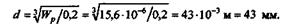
Округляя найденное значение диаметра до ближайшего большего стандартного значения, принимаем d = 45 мм.

Пример 22.4. Сравнить массы сплошного и полого валов, работающих при всех прочих равных условиях (передаваемая мощность, материал, допускаемое напряжение, условия работы), если диаметр сплошного вала d = 70мм, а отношение внутреннего и наружного диаметров полого вала d/D = 0,9.

229

Решение. Из расчетной формулы на кручение круглого цилиндра

видно, что при всех прочих равных условиях моменты сопротивления кручению сплошного и полого валов будут равны, т.е.

Так как по условию d = 70 мм, a d₀ = 0,9 Д то получим равенство

Отсюда

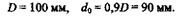
Массы сплошного и полого валов относятся как площади А_с и А_пих поперечных сечений.

Вычислим эти площади:

Разделив первое равенство на второе, получим

Полый вал легче сплошного в 2,58 раза.

Потенциальная энергия деформации

При кручении

Представим себе круглый цилиндрический брус постоянного сечения, жестко защемленный одним концом и нагруженный на другом конце моментом, приложенным статически, т. е. медленно возрастающим от нуля до какого-то значения Т.Полагаем, что момент остается в пределах, когда нагрузка и деформация пропорциональны, т. е. справедлив закон Гука.

Момент T вызывает в брусе деформацию кручения и при этом совершает работу W, которая аккумулируется в виде потенциальной энергии деформации U,причем, пренебрегая незначительными потерями энергии, можно считать, что

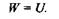
Как известно из теоретической механики, работа в случае статического нагружения равна

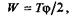
где 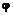— полный угол закручивания бруса. Так как Т = М_к, то

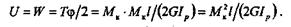
230

При одновременном действии нескольких моментов или ступенчатом изменении размеров поперечного сечения брус разбивают на участки и потенциальную энергию деформации всего бруса определяют как сумму потенциальных энергий отдельных его участков:

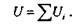
Анализируя полученную в этом параграфе формулу, можно сделать выводы, аналогичные выводам § 19.5.

Дата добавления: 2018-04-15; просмотров: 1364; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 53 54 55 56 575859 60 61 62 Следующая ⇒

Мы поможем в написании ваших работ!