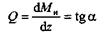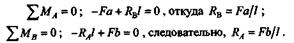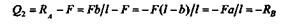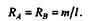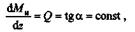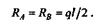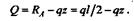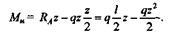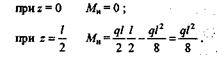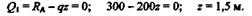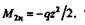Дифференциальные зависимости при изгибе
Между изгибающим моментом, поперечной силой и интенсивностью распределенной нагрузки существуют дифференциальные зависимости, основанные на теореме Журавского, названной по имени замечательного русского инженера-мостостроителя Д. И. Журавского (1821—1891). Эта теорема формулируется так: поперечная сила равна первой производной от изгибающего момента по абсциссе сечения балки.
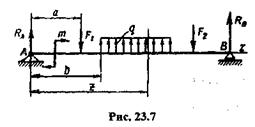
Рассмотрим балку (рис. 23.7). Начало координат возьмем на левом конце балки, а ось z направим вправо (в дальнейшем это будет иметь существенное значение).
237
|
|
На одном из участков балки возьмем сечение с текущей координатой z и запишем уравнение изгибающего момента:
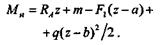
|
|
|
|
| Продифференцировав это выражение по координате z, получим |
| Выражение, стоящее в правой части этого равенства, есть поперечная сила Q в сечении z.Таким образом, |
теорема доказана.
Если уравнение изгибающих моментов (для участков с равномерно распределенной нагрузкой) продифференцировать вторично, то получим
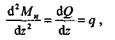
т. е. вторая производная от изгибающего момента или первая производная от поперечной силы по абсциссе сечения балки равна интенсивности распределенной нагрузки.
Как известно из высшей математики, по знаку второй производной функции можно судить о выпуклости или вогнутости кривой; соответствующее правило следует использовать при построении эпюр.
Эпюры поперечных сил
И изгибающих моментов
Для наглядного изображения распределения вдоль оси балки поперечных сил и изгибающих моментов строят эпюры, которые дают возможность определить предположительно опасное сечение балки и установить значения поперечной силы и изгибающего момента в этом сечении.
Эпюры поперечных сил и изгибающих моментов можно строить двумя способами.
Первый способ заключается в том, что сначала составляют аналитические выражения поперечных сил и изгибающих моментов для каждого участка как функций текущей координаты z поперечного сечения:
238
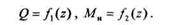
Затем по полученным уравнениям строят эпюры.
Второй способ заключается в построении эпюр по характерным точкам и значениям поперечных сил и изгибающих моментов на границах участков. Применяя этот способ, в большинстве случаев можно обойтись без составления уравнений поперечных сил и изгибающих моментов. При наличии некоторого опыта второй способ предпочтительнее.
При построении эпюр следует руководствоваться приведенными ниже правилами:
1. Эпюру моментов строят на сжатом волокне,т. е. положительные моменты (и положительные поперечные силы) откладывают вверх от оси, а отрицательные — вниз.
2. Пользуясь принципом смягченных граничных условий, будем полагать, что в сечении, где приложена сосредоточенная сила, значение поперечной силы меняется скачкообразно,причем скачок равен модулю этой силы.
3. На том же основании будем полагать, что в сечении, где приложена пара сил (момент), значение изгибающего момента меняется скачкообразно, причем скачок равен моменту пары.
4. Правильность построения эпюр следует проверять с помощью
теоремы Журавского.
|
|
| где |
|
|
Как известно из математики, если Ми = f (z), то
(масштабы Ми и z полагаем численно равными единице), следовательно, если угол а острый, то Q > 0 и изгибающий момент на участке возрастает; если угол а тупой, то Q < 0 и изгибающий момент на участке убывает; если а = 0 на всем участке, то Ми = const, Q = 0 и на этом участке возникает чистый изгиб; если а = 0 в одной точке эпюры моментов, то в этом сечении Q = 0, а изгибающий момент имеет экстремальное (максимальное или минимальное) значение. В сечении, где на эпюре поперечных сил имеется скачок, на эпюре изгибающих моментов будет резкое изменение направления касательной.
Чтобы правила знаков для изгибающих моментов и поперечных сил не противоречили знакам, полученным на основании теоремы Журавско-
239
го, при проверке эпюр следует ось z мысленно всегда направлять слева направо.
5. На участке, где нет распределенной нагрузки, эпюра моментов, вообще говоря, представляет собой наклонную прямую, а эпюра поперечных сил — прямую, параллельную оси.
6. На участке, где приложена равномерно распределенная нагрузка, эпюра моментов представляет собой параболу, а эпюра поперечных сил — наклонную прямую.
7. На конце балки изгибающий момент равен нулю, если там не приложена пара сил.
8. При построении эпюры для консольных балок начало координат удобно брать на конце консоли, что нередко дает возможность обойтись без определения опорных реакций. В сечении, соответствующем заделке, поперечная сила равна реактивной силе, а изгибающий момент — реактивному моменту.
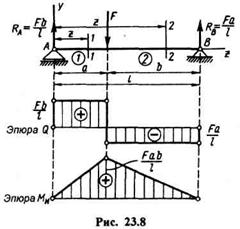
Пример 23.1. Построить эпюры поперечных сил и изгибающих моментов для балки, шарнирно закрепленной двумя концами и нагруженной сосредоточенной силой (рис. 23.8).
Решение. Начало координат поместим на левом конце балки, а ось направим вправо. Данная балка состоит из двух участков.
Определим опорные реакции RAи RВ> составив уравнения моментов относительно опор А и В:
|
|
|
|
Проверим правильность определения реакций, составив уравнение проекций наось y:
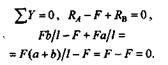
Полученное тождество 0 = 0 говорит о том, что реакции определены правильно.
Приступаем к построению эпюр, применяя для этого метод сечений.
Построение эпюры поперечных сил. На первом участке поперечная сила Q1 положительна, постоянна и равна RА, так как слева о сечения 1—1 других сил нет.
240
|
|
| Откладываем вверх от оси эпюры в произвольном масштабе Q1= RA =Fb/l; затем проводим прямую, параллельную оси эпюры. Значение поперечной силы на втором участке будет равно Q2,где |
(то же получим, если рассмотрим часть балки, расположенную справа от сечения 2—2).
В точке приложения сосредоточенной силы F эпюра Q имеет скачок, численно равный F.
Вид эпюры Q показан на рис.23.8.
Построение эпюры изгибающих моментов. В сечении 1—1 на первом участке изгибающий момент равен М1и = RА z, причем z изменяется от 0 до а.Поскольку z входит в это уравнение в первой степени, эпюра моментов будет представлять собой прямую линию.
Для построения эпюры М1и достаточно найти значения моментов на границах участка, т.е. при z = 0 и z = а:
при z= 0 М1и=0; при z = а М1и =Fba/l.
Для определения изгибающего момента в сечении 2 — 2 проще рассмотреть правую часть балки, на которую действует одна сила:
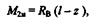
причем z меняется от а до l.
Эпюра моментов на втором участке также будет изображаться прямой линией. Найдем значения изгибающего момента на границах участка:
при z = а М1и= Fa(l - а)/l= Fab/l;
при z = l M2и = Fa(l - l)/l = 0.
По полученным значениям строим эпюру М и.Наибольшее значение Ми будет иметь в сечении, где приложена сила F.
|
|
Ми max = Fab/l.
Это сечение будет предположительно опасным.
В частном случае, когда сила F приложена в середине балки,
а=b = l/2 и Ми max =Fl/4.
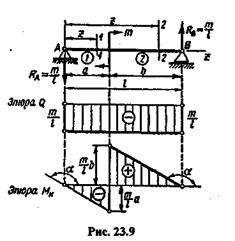
Пример 23.2. Построить эпюры поперечных сил и изгибающих моментов для балки, шарнирно закрепленной двумя концами и нагруженной парой сил с моментом т (рис. 23.9).
Решение. Выберем начало координат на левой опоре, а ось z направим вправо. Балка имеет два участка. Так как пару сил можно уравновесить только парой, то
|
|
Построение эпюры поперечных сил. Для всех сечений первого и второго участков поперечная сила Q будет постоянна, отрицательна и равна Q = RA = - т/1. Следовательно, эпюра будет прямой линией, параллельной оси.
Построение эпюры изгибающих моментов. На первом участке М1и= - RA z, причем z меняется от 0 до а:
при z = 0 М1и = 0;
при z = а М1и= -RAa = -та/l.
На втором участке М2и = -RA z + т,причем z меняется от а до l:
при z= а М2и =- RA a +m= -ma/l + m = mb/1;
при z = l М2и = -RA l+m= - (m/J)/l + m = 0.
Эпюру Мичасто можно построить не составляя уравнений по значениям Ми на границах участков.
Пользуясь ранее приведенными правилами, устанавливаем, что на концах балки Ми = 0; в сечениях, бесконечно близких к паре сил слева и справа от нее, изгибающий момент будет
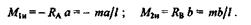
В точке приложения пары сил эпюра Миимеет «скачок», величина которого равна моменту пары.
Построенная по найденным значениям эпюра Мипоказана на рис.23.9. Заметим, что на основании теоремы Журавского
|
|
следовательно, наклонные линии эпюры Мина обоих участках должны быть параллельны между собой.
Полагая b > а,находим наибольшее значение изгибающего момента:
|
|
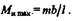
В частном случае, когда внешний момент т приложен в середине пролета балки,
а = b = l/2 и Ми max = + т/2 .
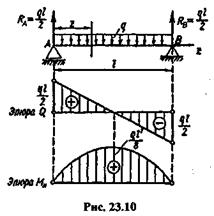
Пример 23.3.Построить эпюры поперечных сил и изгибающих моментов для балки, свободно лежащей на двух опорах и нагруженной равномерно распределенной нагрузкой интенсивности q (рис.23.10).
Решение.В силу симметричности распределения нагрузки по всей длине балки опорные реакции равны между собой:
242
|
|
|
|
| Построение эпюры поперечных сил. Данная балка имеет один участок. В любом сечении поперечная сила |
Поскольку z входит в это уравнение в первой степени (линейная зависимость), то эпюра Q будет прямолинейной. Для построения эпюры достаточно значений поперечной силы в двух точках:
при z = 0 Q = ql/2;
при z = l Q= ql/2-ql= -ql/2.
Эпюра Q показана на рис. 23.10.
|
|
| Это уравнение параболы. Вычислим значения Ми: |
|
|
Построение эпюры изгибающих моментов. Выражение для изгибающего момента в любом сечении балки имеет вид
Очевидно, что при z = l Ми = 0.
По найденным значениям строим эпюру Ми,как показано на рис. 23.10.
Поскольку вторая производная
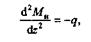
т. е. меньше нуля, то эпюра Ми будет расположена выпуклостью вверх.
Согласно теореме Журавского максимальное значение изгибающего момента будет в середине пролета балки, где Q = 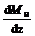 = 0
= 0
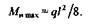
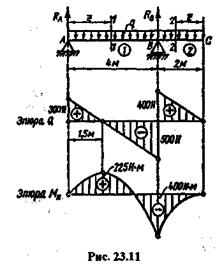
Пример 23.4. Построить эпюры поперечных сил и изгибающих моментов для консольной балки АС,свободно лежащей на двух опорах и нагруженной равномерно распределенной нагрузкой интенсивности q = 200 Н  м, как показано на рис. 23.11.
м, как показано на рис. 23.11.
Решение. Определим реакции RАи RВ:
243
|
|
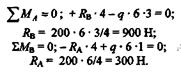
Переходим к построению эпюры Q.Балка имеет два участка.
На первом участке поперечная сила Q1 = RА- qz,причем z меняется от 0 до 4 м
при z = 0 Q1= RА = 300Н;
при z= 4м Q1 = 300-200  4 =
4 =
= 300 - 800 = -500 Н.
Для упрощения построения эпюры Q на втором участке возьмем начало координат в точке С и направим ось z влево, тогда Q2= qz,причем z меняется от 0 до 2 м
при z = 0 Q2 = 0;
при z = 2м Q2= 200  2 = 400Н.
2 = 400Н.
На границе участков в точке В эпюра Q имеет «скачок», равный по величине опорной реакции Rв = 900 Н.
Найдем точку оси, в которой Q = 0. Для этого запишем
|
|
На основании теоремы Журавского можно ожидать в этой точке экстремальное значение изгибающего момента. Переходим к построению эпюры Ми. На первом участке выражение для изгибающего момента имеет вид
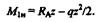
Эпюра Мибудет представлять собой параболу. Вычислим значения М1ив трех точках:
при z = 0 М1и= 0;
при z = 1,5 м М1и= 300  1,5 -200
1,5 -200  1,52/2 = 450 - 225 = 225 Нм; при z = 4м М1и= 300
1,52/2 = 450 - 225 = 225 Нм; при z = 4м М1и= 300  4-200
4-200  42/2 = 1200-1600 = -400Нм. Для второго участка, взяв за начало координат точку С, получим
42/2 = 1200-1600 = -400Нм. Для второго участка, взяв за начало координат точку С, получим
|
|
Вычислим М2ина границах участка:
при z = 0 М2и = 0;
при z = 2м М2и= -200  22/2 = -400Н
22/2 = -400Н  м.
м.
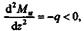 По найденным значениям строим эпюру Ми.
По найденным значениям строим эпюру Ми.
| Поскольку в данном примере |
эпюра Мина обоих участках
будет направлена выпуклостью вверх.
Из построенных эпюр видно, что опасным будет сечение балки на опоре В.
244
Дата добавления: 2018-04-15; просмотров: 795; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

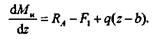
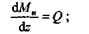
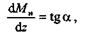
 — угол, который составляет касательная к эпюре моментов с положительным направлением оси z.Согласно теореме Журавского,
— угол, который составляет касательная к эпюре моментов с положительным направлением оси z.Согласно теореме Журавского,