ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ПЛОСКИХ СЕЧЕНИЙ
Статический момент площади
|
|
При некоторых деформациях прочность деталей зависит не только от площади поперечного сечения, но и от его формы. До сих пор мы изучали деформации, у которых напряжения зависели только от площади поперечного сечения. В дальнейшем для изучения деформаций кручения и изгиба нам потребуется знание некоторых других геометрических характеристик плоских фигур.
Статическим моментом площади плоской фигуры относительно оси,
лежащей в той же плоскости, называется взятая по всей площади сумма произведений площадей элементарных площадок на расстояния от них до этой оси (рис. 21.1).
Статический момент площади обозначим S с индексом соответствующей оси:
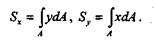
В теоретической механике мы вывели формулы для определения координат центра тяжести площади фигуры:
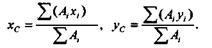
Так как в этих формулах под Ai можно понимать площадь dA элементарной площадки, то в пределе при dA, стремящемся к нулю, выражения, стоящие в числителях правых частей формул, будут представлять собой статические моменты площади фигуры относительно осей у и х,a  есть площадь А всей фигуры. Следовательно,
есть площадь А всей фигуры. Следовательно,

Статический момент площади фигуры относительно оси, лежащей в этой же плоскости, равен произведению площади фигуры на расстояние ее центра тяжести до этой оси.
Единица статического момента площади
|
|
Статический момент площади фигуры может быть величиной положительной, отрицательной и равной нулю.
Очевидно, что статический момент площади относительно оси, проходящей через центр тяжести площади фигуры (центральной оси), в том числе относительно оси симметрии фигуры, равен нулю.
В теоретической механике мы установили также, что в формулах для определения координат центра тяжести площади под Аi можно понимать площади конечных частей фигуры, а под xi и yi — координаты центров тяжести этих частей (т. е. применять метод разбиения). Отсюда следует, что при определении статического момента площади сложной фигуры также можно применять метод разбиения, т. е. определять статический момент всей фигуры как алгебраическую сумму статических моментов отдельных ее частей:
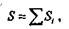
где Si— статический момент площади каждой части фигуры.
Понятие о статическом моменте площади понадобится нам в дальнейшем для определения положения центров тяжести сечений и при определении касательных напряжений при изгибе.
Полярный момент инерции
Полярным моментом инерции плоской фигуры относительно полюса, лежащего в той же плоскости, называется взятая по всей площади сумма произведений площадей элементарных площадок на квадраты их расстояний до полюса (рис. 21.1).
|
|
| Единица полярного момента инерции |
|
|
Полярный момент инерции обозначим
Полярный момент инерции — величина всегда положительная и не равная нулю.
216
|
|
Так как понятие полярного момента инерции понадобится нам при изучении деформаций кручения круглых валов, то выведем формулы для определения полярных моментов инерции круглого сплошного и кольцевого сечений, принимая за полюс центры этих фигур.
1. Круг диаметром d (рис. 21.2).
Выделим бесконечно малую площадку dА в виде кольца шириной d  , находящегося на
, находящегося на
расстоянии р от полюса (  — переменная величина). Тогда dА = 27
— переменная величина). Тогда dА = 27 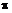
 d
d  . Вычислим полярный момент инерции:
. Вычислим полярный момент инерции:
|
|
Полярный момент инерции кольцевого сечения можно вычислить как разность полярных моментов инерции большого и малого кругов.
Осевой момент инерции
Осевым моментом инерции плоской фигуры относительно оси, лежащей в той же плоскости, называется взятая по всей площади сумма произведений площадей элементарных площадок на квадрат расстояний от них до этой оси (см. рис. 21.1).
Осевой момент инерции обозначим I с индексом, соответствующим оси:

Очевидно, что осевой и полярный моменты инерции выражаются в одинаковых единицах:

Осевой момент инерции — величина всегда положительная и не равная нулю.
217
|
|
Сложим моменты инерции относительно двух взаимно перпендикулярных осей x и у (см. рис.21.1):
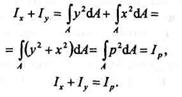
Сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей равна полярному моменту инерции относительно начала координат. Так как интеграл суммы равен сумме интегралов, то момент инерции сложной фигуры можно вычислять как сумму моментов инерции простых фигур,на которые разбивают сложную фигуру. Понятие об осевых моментах инерции понадобится нам в дальнейшем при изучении теории изгиба.
Вычислим осевые моменты инерции некоторых простых фигур.
1. Прямоугольник b 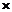 h (рис. 21.3).
h (рис. 21.3).
Бесконечно малую площадку dA выделим в виде полоски шириной b и высотой dy,тогда dA = bdy:
|
|
Для квадрата со стороной а 
2. Крут диаметром d относительно осей х и у. В силу симметрии для
круга 1х=1у.Так как
|
|
то
218


3. Кольцо размером D 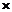 d относительно осей х и у:
d относительно осей х и у:
Момент инерции
Дата добавления: 2018-04-15; просмотров: 372; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!









