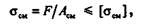Смятие. Контактные напряжения
Если детали конструкции, передающие значительную сжимающую нагрузку, имеют небольшую площадь контакта, то может произойти смятие поверхностей деталей. Для предотвращения смятия, например, под гайки и головки болтов подкладывают шайбы (рис. 19.12).
Для простоты расчетов полагают, что при контакте по плоскости возникают нормальные напряжения смятия, равномерно распределенные по площади контакта. Расчетное уравнение на смятие имеет вид
|
|
где F — сжимающая сила; [ 
см] — допускаемое напряжение на смятие; Асм— площадь контакта.
Если соприкасающиеся детали сделаны из разных материалов, то на смятие проверяют деталь из более мягкого материала.
При контакте двух деталей по цилиндрической поверхности (например, заклепочное соединение) закон распределения напряжений смятия по поверхности контакта сложен (рис. 19.13, а), поэтому при расчете на смятие цилиндрических отверстий в расчетную формулу подставляют не площадь боковой поверхности полуцилиндра, по которой происходит контакт, а значительно меньшую площадь диаметрального сечения отверстия (условная площадь смятия); тогда
|
|
|
|
|
|
204
|
|
где d — диаметр отверстия;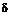 
— толщина соединяемой детали (высота цилиндра).
При различной толщине соединяемых деталей в расчетную формулу подставляют меньшую толщину.
В машиностроении допускаемые напряжения на смятие для болтовых, штифтовых и шпоночных соединений из низкоуглеродистой стали принимают в пределах 100...120 МПа, для клепаных соединений — 240...320 МПа, для древесины (сосна, дуб) — 2,4...11 МПа в зависимости от сорта древесины и направления сжимающей силы по отношению к направлению волокон.
|
|
|
Пример 19.6.Тяга 1 соединена с вилкой 2 посредством болта, поставленного без зазора, (рис. 19.13, б). Определить напряжения смятия в головке тяги, если сила F = 48кН, диаметр болта d = 20 мм, а толщина головки тяги 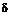= 24 мм.
Решение. Вычисляем условную площадь смятия:
Определяем напряжения смятия в головке тяги:
|
|
|
|
Контактные напряжения. Контактными называются напряжения и деформации, возникающие при сжатии тел криволинейной формы, причем первоначальный контакт может быть линейным (например, сжатие двух цилиндров с параллельными образующими) или точечным (например, сжатие двух шаров). В результате деформации контактирующих тел начальный точечный или линейный контакт переходит в контакт по некоторой малой площадке. Решение вопросов о контактных напряжениях и деформациях впервые дано в работах немецкого физика Г.Герца (1857—1894).
Для деталей, в поверхностных слоях которых возникают контактные напряжения (например, фрикционные катки, зубчатые колеса, подшипники качения), решающую роль играет прочность рабочих поверхностей — контактная прочность.
|
|
|
Рассмотрим наиболее важный для нас случай контакта двух цилиндров с параллельными образующими (рис. 19.14). Определение контактных напряжений в этом случае производится по
205
формуле Герца, выведенной в предположении, что материалы цилиндров подчиняются закону Гука. Очевидно, что контактные напряжения по ширине площадки контакта неравномерны. Максимальные напряжения н вычисляются по формуле
где q — нагрузка на единицу длины линии контакта; v — коэффициент Пуассона, Епр — приведенный модуль упругости, получаемый из соотношения 
, (1/Е — некоторая характеристика податливости материала), откуда
рпр — приведенный радиус кривизны цилиндров, определяемый из соотношения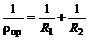 
(1/ 
—кривизна поверхности), откуда
При v = 0,3 формула Герца приобретает вид
Глава 20
СДВИГ (СРЕЗ)
Напряжения при сдвиге
Сдвигом называется такой вид деформации, при которой в любом поперечном сечении бруса возникает только поперечная сила. Деформацию сдвига можно наблюдать, например, при резке ножницами металлических полос или прутков (рис. 20.1, а).
|
|
|
Рассмотрим брус площадью поперечного сечения А,перпендикулярно оси которого приложены две равные и противоположно направленные силы F; линии действия их параллельны и находятся на отно-
206
сительно небольшом расстоянии друг от друга. Для определения поперечной силы Q применим метод сечений (рис. 20.1, б).
|
|
|
|
| откуда определим поперечную силу |
|
|
Во всех точках поперечного сечения действуют распределенные силы, равнодействующую которых определим из условия равновесия оставленной части бруса:
Поперечная сила есть равнодействующая внутренних касательных сил в поперечном сечении при сдвиге.
Естественно считать, что при сдвиге в поперечном сечении бруса действуют только касательные напряжения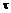 
. Предполагаем, что эти напряжения распределены по сечению равномерно и, следовательно, их можно вычислить по формуле
Очевидно, что при сдвиге форма сечения на значение напряжения не влияет.
Примечание. Изложенный в этом параграфе расчет касательных напряжений при сдвиге приближенный, так как линии действия сил F и Q (рис. 20.1, б)не направлены по одной прямой и, строго говоря, эти силы не являются уравновешенной системой, а представляют собой пару сил. Однако момент этой пары (ввиду малого плеча) невелик и соответствующими ей напряжениями можно пренебречь.
|
|
|
Дата добавления: 2018-04-15; просмотров: 1734; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!