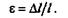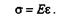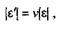Напряжения и продольная деформация

При растяжении и сжатии

Растяжением или сжатием называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только продольная сила. Брусья с прямолинейной осью (прямые брусья), работающие на растяжение или сжатие, часто называют стержнями.

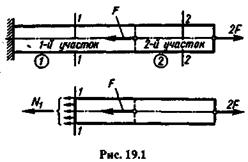
Рассмотрим невесомый, защемленный левым концом прямой брус, вдоль оси которого действуют активные силы F и 2F(рис. 19.1).

Части бруса постоянного сечения, заключенные между поперечными плоскостями, в которых приложены активные или реактивные силы, будем называть участка-ми. Изображенный на рис. 19.1 брус состоит из двух участков.

Применив метод сечений, определим продольные силы N₁и N₂на участках. Рассечем брус на первом участке поперечным сечением 1—1.Во всех точках бруса будут

186

действовать внутренние распределенные силы, равнодействующая которых определится из условия равновесия одной из частей бруса (например, правой от сечения):

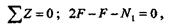
откуда

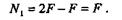
Мы видим, что для равновесия оставленной части бруса в сечении

1—1необходимо приложить только силу N_1,направленную вдоль оси, т. е. продольную силу.

Продольная сила есть равнодействующая внутренних нормальных сил, возникающих в поперечном сечении бруса. Нетрудно понять, что в сечении 2—2 на втором участке продольная сила будет иметь другое значение: N₂ = 2F.Таким образом, продольная сила в поперечном сечении бруса численно равна алгебраической сумме внешних сил, расположенных по одну сторону сечения (имеется в виду, что все силы направлены вдоль оси бруса).

Очевидно, что в пределах одного участка продольная сила будет иметь постоянное значение. Следует помнить, что, рассматривая равновесие части бруса, расположенной не справа, а слева от сечения, мы должны были ввести в уравнение равновесия реакцию защемленного конца, определенную путем рассмотрения равновесия всего бруса.

В дальнейшем растягивающие (направленные от сечения) продольные силы мы будем считать положительными, а сжимающие (направленные к сечению) — отрицательными.

Иначе говоря, если равнодействующая внешних сил, приложенных к левой части бруса, направлена налево, а приложенных к правой части — вправо, то продольная сила в данном сечении будет положительной,и наоборот.

При изучении ряда деформаций мы будем мысленно представлять себе брусья состоящими из бесчисленного количества волокон, параллельных оси, и предполагать, что при деформации растяжения и сжатия волокна не надавливают друг на друга (это предположение называется гипотезой о ненадавливании волокон).

Если изготовить прямой брус из резины (для большей наглядности), нанести на его поверхности сетку продольных и поперечных линий и подвергнуть брус деформации растяжения, то можно отметить следующее: 1) поперечные линии останутся в плоскостях, перпендикулярных оси, а расстояния между ними увеличатся; 2) продольные линии останутся прямыми, а расстояния между ними уменьшатся.

Из этого опыта можно сделать вывод, что при растяжении справедлива гипотеза плоских сечений и, следовательно, все волокна бруса удлиняются на одну и ту же величину.

187

Все сказанное выше позволяет сделать вывод, что при растяжении и сжатии в поперечных сечениях бруса возникают только нормальные напряжения, равномерно распределенные по сечению и вычисляемые по формуле

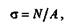
где N— продольная сила; А — площадь поперечного сечения. Очевидно, что при растяжении и сжатии форма сечения на напряжение не влияет.

В сечениях, близких к точкам приложения растягивающих или сжимающих сил, закон распределения напряжений по сечению будет более сложным, но пользуясь принципом смягченных граничных условий, мы будем этими отклонениями пренебрегать и считать, что во всех сечениях бруса напряжения распределены равномерно и что в сечении, где к брусу приложена вдоль оси сосредоточенная сила, значения продольной силы и напряжений меняются скачкообразно.

Для наглядного изображения распределения вдоль оси бруса продольных сил и нормальных напряжений строят графики, называемые эпюрами, причем для нормальных напряжений применяется то же правило знаков, что и для продольных сил.

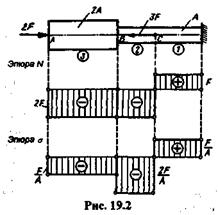
Пример 19.1.Построить эпюры продольных сил и нормальных напряжений для ступенчатого бруса, изображенного на рис. 19.2.

Решение. Разобьем брус на три участка. Границами участков являются сечения, в которых приложены внешние силы, и места изменения размеров поперечного сечения.

Для построения эпюры продольных сил N под рисунком бруса проводим ось эпюры, параллельную оси бруса. Величины продольных сил в произвольном масштабе откладываем перпендикулярно оси эпюры, причем положительные значения N (растяжение) откладываются вверх, а отрицательные (сжатие) — вниз от оси. Эпюру отштриховывают, как показано на рисунке. В точках приложения сил на эпюре N получаются скачкообразные изменения, причем величина «скачка» равна модулю приложенной в сечении бруса силы.

Применяя метод сечений, устанавливаем, что во всех поперечных сечениях первого и второго участков действует продольная сила N₁ = -2F = N₂.Откладываем вниз от оси эпюры величину 2F в произвольном масштабе и проводим прямую, параллельную оси эпюры. В сечении С бруса приложена сила 3F.Применяя метод сечений, устанавливаем, что во всех поперечных сечениях третьего

участка действует продольная сила N₃ = F. Очевидно, что значение ординаты эпюры продольных сил под заделкой равно реакции заделки. Отметим, что применяя метод сечений, выгоднее рассматривать равновесие части бруса, расположенной со стороны его свободного конца, в противном случае необходимо заранее определять и вводить в уравнение равновесия реакцию заделки.

Для построения эпюры а определим нормальные напряжения на участках бруса. Тогда на первом участке нормальные напряжения будут ₁= -2F/2A = -F/A,на втором ₂ =-2F/A, на третьем ₃=F/A. Правила построения эпюры а те же, что и для эпюры N.

Для расчетов на прочность особый интерес представляют те сечения бруса, в которых напряжения являются по абсолютному значению максимальными. Эти сечения являются предположительно опасными. В нашем примере такими будут сечения бруса на втором участке.

Перейдем к рассмотрению деформаций. Представим себе прямой брус постоянного поперечного сечения А,длиной l, жестко защемленный одним концом и нагруженный на другом конце растягивающей силой F (рис. 19.3). Под действием этой силы брус удлинится на некоторую величину l, которую назовем абсолютным удлинением. Отношение абсолютного удлинения l к первоначальной длине l назовем относительным удлинением и обозначим :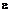

Относительное удлинение 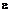— число отвлеченное, иногда его выражают в процентах:

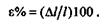
Вследствие деформации поперечные сечения бруса перемещаются в направлении оси. Взаимное перемещение двух сечений равно изменению длины части бруса, заключенной между этими сечениями.

Итак, деформация бруса при растяжении и сжатии характеризуется абсолютным и относительным удлинением или укорочением.

§19.2. Закон Гука при растяжении и сжатии

Напряжения и деформации при растяжении и сжатии связаны между собой зависимостью, которая называется законом Гука, по имени установившего этот закон английского физика Роберта Гука (1635—1703).

189

Закон Гука при растяжении и сжатии справедлив лишь в определенных пределах нагружения и формулируется так: нормальное напряжение прямо пропорционально относительному удлинению или укорочению.

Математически закон Гука можно записать в виде равенства:

Коэффициент пропорциональности Е характеризует жесткость материала, т. е. его способность сопротивляться упругим деформациям растяжения или сжатия, и называется модулем продольной упругости илимодулем упругости первого рода.

Модуль упругости и напряжение выражаются в одинаковых единицах:

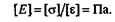
Значения Е,МПа, для некоторых материалов:

Чугун........................................................ (1,5...1,6) 10⁵

Сталь........................................................ (1,96... 2,16) 10⁵

Медь.......................................................... (1,0...1,3) 10⁵

Сплавы алюминия................................... (0,69...0,71) 10⁵

Дерево (вдоль волокон)............................ (0,1...0,16) 10⁵

Текстолит................................................. (0,06...0,1) 10⁵

Капрон .................................................... (0,01...0,02) 10⁵

Если в формулу закона Гука подставим выражения

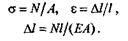
то получим

Произведение ЕА, стоящее в знаменателе, называется жесткостью сечения при растяжении и сжатии; оно характеризует одновременно физико-механические свойства материала и геометрические размеры поперечного сечения бруса.

Эта формула читается так: абсолютное удлинение или укорочение прямо пропорционально продольной силе, длине и обратно пропорционально жесткости сечения бруса.

Отношение ЕА/l называется жесткостью бруса при растяжении или сжатии.

Приведенные выше формулы закона Гука применимы только для брусьев или их участков постоянного поперечного сечения, изготовленных из одного материала и при постоянной продольной силе.

Для бруса, имеющего несколько участков, отличающихся материалом, размерами поперечного сечения, продольной силой, изменение длины всего бруса равно алгебраической сумме удлинений и укорочений отдельных участков:

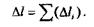
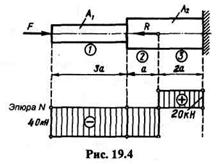
Пример 19.2. На стальной ступенчатый брус действуют силы F = 40 кН и R = 60 кН. Площади поперечных сечений равны А₁= 800 мм², А₂ = 1600 мм². Длины участков указаны на рис. 19.4; а = 0,2 м. Определить изменение длины бруса двумя способами: 1) с помощью эпюры продольных сил; 2) с помощью принципа независимости действия сил. Принять Е = 2 10¹¹ Па.

Решение. 1-й способ. Разобьем брус на участки и, применяя метод сечений, определим значения продольных сил на каждом из них:

N₁ = N₂= -40 кН (сжатие), N₃= 20 кН (растяжение). Строим эпюру продольных сил.

Для бруса, состоящего из нескольких участков, l= l ₁+ l₂ + l₃, где по закону Гука

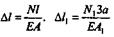— изменение длины первого участка; аналогич-

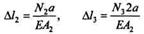но,

Следовательно,

— изменение длин второго и третьего участков.

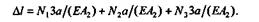
Подставив числовые значения с учетом знаков продольных сил, получим

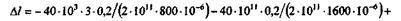
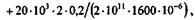
откуда

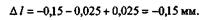
Следовательно, брус укоротился на 0,15 мм.

2-й способ. Решим этот пример с помощью принципа независимости действия сил. Изменение длины бруса l будет складываться из укорочения l_F всего бруса под действием силы F и удлинения l_Rтретьего участка под действием сипы R:

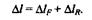
Вычислим каждое из этих слагаемых:

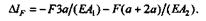
Подставляя числовые значения, получаем l_F= -0,225 мм.

Аналогично находим

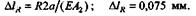
Отсюда

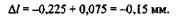
Решая задачу двумя способами, мы получили один и тот же результат, что свидетельствует о правильности решения.

191

Поперечная деформация

При растяжении и сжатии

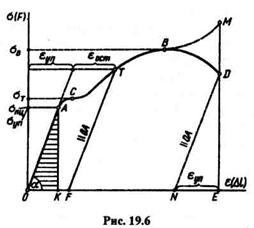
Описанный в § 19.1 опыт с резиновым брусом показывает, что поперечные размеры сечения при растяжении уменьшаются, а при сжатии увеличиваются. Это характерно для растяжения и сжатия всех материалов. Опытным путем установлено, что при одноосном растяжении или сжатии отношение относительных поперечной и продольной деформаций есть для данного материала величина постоянная. Впервые зависимость между относительной поперечной 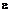' и относительной продольной е деформациями была установлена французским ученым Пуассоном (1781—1840). Эта зависимость имеет следующий вид:

где v — коэффициент поперечной деформации, называемый к о э ф ф и -циентом Пуассона.

Нетрудно понять, что v — величина безразмерная.

Коэффициент Пуассона, как и модуль упругости первого рода, зависит только от материала и характеризует его упругие свойства. При растяжении и сжатии коэффициент Пуассона полагают одинаковым.

Значения v для некоторых материалов:

Пробка................ 0,00 Латунь.................... 0,32...0,42

Чугун.................. 0,23...0,27 Свинец.................... 0,42

Сталь ................. 0,24...0,30 Каучук ................... 0,47

Медь................... 0,31-0,34 Парафин ................ 0,5

Пример 19.3. Стальной цилиндр (рис. 19.5) длиной l = 100 мм и диаметром d = 40 мм при сжатии укорачивается до размера l₁= 99,9 мм, а диаметр его увеличивается до размера d₁ = 40,01 мм. Найти коэффициент Пуассона v.

Решение. Определим относительную продольную и поперечную деформацию | 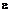| и | 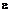'|, если l= l –

– l₁= 0,1 мм , a d= d₁ - d = 0,01 мм, тогда

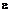l/l=| |, d/d=| '|.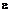

Отсюда коэффициент Пуассона

v = | 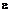'/ 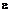|= l d/(d l).

Подставляя числовые значения, получим

v = 100 0,01/(40 0,1) = 0.25.

Диаграмма растяжения

Низкоуглеродистой стали

Механические характеристики материалов, т. е. величины, характеризующие их прочность, пластичность, упругость, твердость, а также упругие постоянные Е и v, необходимые конструктору для выбора материалов и расчетов проектируемых деталей, определяют путем механических испытаний стандартных образцов, изготовленных из исследуемого материала.

Большая заслуга в установлении единообразных во всем мире методов испытания материалов принадлежит русскому профессору Н. А. Беле-любскому (1845—1922) — президенту Международного общества испытания материалов.

Вопросы проведения лабораторных испытаний материалов в настоящей книге не излагаются, с ними читатель может ознакомиться в специальных учебных пособиях.

В данном параграфе мы подробно рассмотрим диаграмму, полученную в процессе наиболее распространенного и важного механического испытания, а именно испытания на растяжение низкоуглеродистой стали (например, стали СтЗ) при статическом нагружении.

В процессе этого испытания специальное устройство испытательной машины автоматически вычерчивает диаграмму, выражающую зависимость между растягивающей силой и абсолютным удлинением, т. е. в координатах (F, l).Для изучения механических свойств материала независимо от размеров образца применяется диаграмма в координатах «напряжение—относительное удлинение» ( , 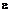). Эти диаграммы отличаются друг от друга лишь масштабами.

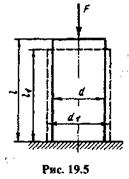
Диаграмма растяжения низкоуглеродистой стали представлена на рис. 19.6. Эта диаграмма имеет следующие характерные точки.

Точка А соответствует пределу пропорциональности.

Пределом про-порциональности _пцназывается то наибольшее напряжение, до которого деформации растут пропорционально нагрузке,

193

т. е. справедлив закон Гука (для стали СтЗ _пц 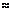200 МПа).

Точка А практически соответствует и другому пределу, который называется пределом упругости.

Пределом упругости уп называется то наибольшее напряжение, до которого деформации практически остаются упругими.

Точка С соответствует пределу текучести.

Пределом текучести _т называется такое напряжение, при котором в образце появляется заметное удлинение без увеличения нагрузки (для стали СтЗ _т 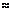240 МПа).

При достижении предела текучести поверхность образца становится матовой, так как на ней появляется сетка линий Людерса—Чернова, наклоненных к оси под углом 45°. Эти линии впервые были описаны в 1859 г. немецким металлургом Людерсом и независимо от него в 1884 г. русским металлургом Д. К. Черновым (1839—1921), предложившим использовать их при экспериментальном изучении напряжений в сложных деталях.

Предел текучести является основной механической характеристикой при оценке прочности пластичных материалов.

Точка В соответствует временному сопротивлению или пределу прочности.

Временным сопротивлением а„ называется условное напряжение, равное отношению максимальной силы, которую выдерживает образец, к первоначальной площади его поперечного сечения (для стали СтЗ _В 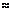400 МПа).

При достижении временного сопротивления на растягиваемом образце образуется местное сужение — шейка, т. е. начинается разрушение образца.

В определении временного сопротивления говорится об условном напряжении, так как в сечениях шейки напряжения будут больше.

Пределом прочности _пчназывается временное сопротивление образца, разрушающегося без образования шейки. Предел прочности является основной механической характеристикой при оценке прочности хрупких материалов.

Точка D соответствует напряжению, возникающему в образце в момент разрыва во всех поперечных сечениях, кроме сечений шейки.

Точка М соответствует напряжению, возникающему в наименьшем поперечном сечении шейки в момент разрыва. Это напряжение можно назвать напряжением разрыва.

С помощью диаграммы растяжения в координатах ( , 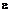) определяем модуль упругости первого рода:

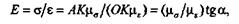
где 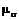— масштаб напряжении; 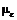— масштаб относительных удлинении;

194

— угол, который составляет с осью абсцисс прямая линия диаграммы до предела пропорциональности.

Для большинства углеродистых сталей предел пропорциональности можно приблизительно считать равным половине временного сопротивления.

Деформация образца за пределом упругости состоит из упругой и остаточной, причем упругая часть деформации подчиняется закону Гука и за пределом пропорциональности (см. рис. 19.6). Если нагрузку снять, то образец укоротится в соответствии с прямой TF диаграммы. При повторном нагружении того же образца его деформация будет соответствовать диаграмме FTBD.Таким образом, при повторном растяжении образца, ранее нагруженного выше предела упругости, механические свойства материала меняются, а именно: повышается прочность (предел упругости и пропорциональности) и уменьшается пластичность. Это явление называется наклёпом.

В некоторых случаях наклеп нежелателен (например, при пробивке отверстий под заклепки увеличивается возможность появления трещин возле отверстий), в других случаях наклеп создается специально (например, цепи подъемных машин, арматура железобетонных конструкций, провода, тросы подвергаются предварительной вытяжке за предел текучести). Проволока, полученная волочением, в результате наклепа имеет значительно большую прочность, чем точеный образец из того же материала.

Степень пластичности материала может быть охарактеризована (в процентах) остаточным относительным удлинением 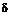и остаточным относительным сужением 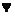шейки образца после разрыва:

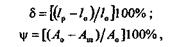
где l_o — первоначальная длина образца; l_р — длина образца после разрыва; А_o— первоначальная площадь поперечного сечения образца; А_ш—площадь наименьшего поперечного сечения шейки образца после разрыва.

Чем больше 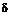и 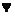, тем пластичнее материал. Материалы, обладающие очень малой пластичностью, называют хрупкими. Диаграмма растяжения хрупких материалов не имеет площадки текучести, у них при разрушении не образуется шейка.

Диаграмма сжатия стали до предела текучести совпадает с диаграммой растяжения, причем результаты испытаний сталей на растяжение и сжатие равноценны.

Результаты испытаний на растяжение и сжатие чугуна значительно отличаются друг от друга; предел прочности при растяжении в

195

3...5 раз ниже, чем при сжатии. Иными словами, чугун значительно хуже работает на растяжение, чем на сжатие.

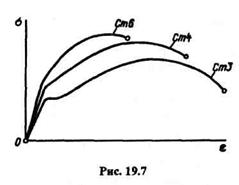
Отметим, что ярко выраженную площадку текучести имеют только диаграммы растяжения низкоуглеродистой стали и некоторых сплавов цветных металлов. На рис. 19.7 показан для сравнения вид диаграмм растяжения сталей с различным содержанием углерода; из рисунка видно, что с повышением процента содержания углерода увеличивается прочность стали и уменьшается ее пластичность.

Для пластичных материалов, диаграммы растяжения которых не имеют ярко выраженной площадки текучести (средне и высокоуглеродистые, легированные стали) или совсем ее не имеют (медь, дюралюминий), вводится понятие условного предела текучести — напряжения, при котором относительное остаточное удлинение образца равно 0,2%. Условный предел текучести также обозначим _т(иногда его обозначают _0,2).

Следует отметить, что деление материалов на пластичные и хрупкие условно, так как в зависимости от характера действующей нагрузки хрупкий материал может получить пластические свойства и, наоборот, пластичный материал приобретает свойства хрупкого. Так, например, деталь из пластичного материала при низкой температуре или при ударной нагрузке разрушается без образования шейки, как хрупкая.

Дата добавления: 2018-04-15; просмотров: 1514; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 43 44 45 46 474849 50 51 52 Следующая ⇒

Мы поможем в написании ваших работ!