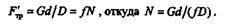Плоской системы произвольно расположенных сил

⇐ ПредыдущаяСтр 10 из 72Следующая ⇒

Изучив свойства главного вектора и главного момента, укажем четыре возможных случая приведения плоской системы произвольно расположенных сил:

1. F_гл0, M_гл0, т. е. главный вектор и главный момент не равны

нулю. В этом случае система сил эквивалентна равнодействующей, которая равна по модулю главному вектору, параллельна ему, направлена в ту же сторону, но по другой линии действия (см. § 5.3, п. 3).

2. F_гл0, M_гл = 0. В этом случае система сил эквивалентна равнодействующей, линия действия которой проходит через центр приведения и совпадает с главным вектором.

3. F_гл=0, M_гл0. В этом случае система эквивалентна паре. Так как модуль и направление главного вектора во всех случаях не зависят от выбора центра приведения, то в рассматриваемом случае величина и знак главного момента тоже не зависят от центра приведения, ибо одна и та же система сил не может быть эквивалентна различным парам.

4. F_гл=0, M_гл = 0. В этом случае система сил эквивалентна нулю, т. е. находится в равновесии.

Аналитические условия равновесия плоской системы произвольно расположенных сил

Согласно § 5.4, плоская система произвольно расположенных сил находится в равновесии, когда и главный вектор, и главный момент равны нулю:

Но F_гл = 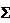F_i и равенство F_гл = 0 означает, что силовой многоугольник, построенный на силах данной системы, должен быть замкнут, следовательно, алгебраическая сумма проекций сил на каждую из двух осей координат х и у должна равняться нулю, т. е.

Главный момент и равенство М_гл = 0 означают, что

алгебраическая сумма моментов сил данной системы относительно любого центра приведения равняется нулю, следовательно,

Итак, для равновесия плоской системы произвольно расположенных сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на оси координат х и у равнялись нулю и чтобы алгебраическая сумма моментов этих сил относительно любой точки плоскости также равнялась нулю.

Условия равновесия упрощенно запишем в виде равенств

Отметим, что выведенные ранее условия равновесия системы сходящихся сил, системы параллельных сил и системы пар являются частными случаями условий равновесия, полученных в этом параграфе.

При решении некоторых задач бывает целесообразно вместо одного или двух уравнений проекций составлять уравнения моментов.

Если заменить одно уравнение проекций, то условия равновесия плоской системы произвольно расположенных сил будут выглядеть так:

Однако следует помнить, что эти условия становятся недостаточными для равновесия, когда центры моментов А и В лежат на одном перпендикуляре к оси х:в этом случае даже при выполнении указанных условий система сил может иметь равнодействующую, проходящую через эти точки, и, следовательно, не быть в равновесии.

Если заменить два уравнения проекций, то условия равновесия плоской системы произвольно расположенных сил будут выглядеть так:

Однако эти условия становятся недостаточными для равновесия, когда центры моментов А, В и С лежат на одной прямой; в этом случае даже при выполнении указанных условий система сил может иметь равнодействующую, проходящую через эти точки, и, следовательно, не быть в равновесии.

Условия равновесия плоской системы параллельных сил являются частным случаем условий равновесия, выведенных в этом параграфе. Если ось у расположить параллельно линиям действия системы параллельных сил, то уравнение равновесия 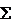X=0 обратится в тождество, а 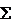Y= 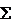F_i, т.е. алгебраическая сумма проекций сил системы на ось у будет равна алгебраической сумме этих сил. Тогда условия равновесия плоской системы параллельных сил запишутся следующим образом:

и сформулируются так: для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы алгебраическая сумма всех сил равнялась нулю и чтобы алгебраическая сумма моментов всех сил относительно любой точки плоскости также равнялась нулю.

Так как все виды аналитических условий равновесия действительны для любых прямоугольных осей координат, то в процессе решения одной задачи или при проверке решения оси координат можно изменить, т. е.

одни уравнения проекций сил составить для одной системы координат, а другие — для новой системы координат. Этот прием в некоторых случаях упрощает решение или проверку решения задач. При этом следует помнить, что число уравнений равновесия, составляемых для решения (но не для проверки решения), не должно быть больше числа условий равновесия, соответствующих системе сил, рассматриваемых в задаче.

При решении задач статики аналитическим способом целесообразно составлять уравнения равновесия так, чтобы в каждом из них была только одна неизвестная величина. Во многих случаях этого можно достигнуть, если рационально выбрать оси координат и центры моментов.

Пример 5.1. Горизонтальная балка, поддерживающая балкон, подвергается действию равномерно распределенной нагрузки интенсивностью q = 2 кН/м (рис. 5.5). На балку у свободного конца С передается нагрузка от колонны Р = 2 кН. Расстояние от оси колонны до стены l = 1,5 м. Определить реакции заделки А.

Решение. Отбросим заделку, заменим ее реакциями и рассмотрим равновесие балки. Реакции стены представляют собой реактивную силу R и реактивный момент т. Реактивная сила вертикальна, так как активные силы, действующие на балку, горизонтальных составляющих не имеют. Распределенную нагрузку заменим ее равнодействующей ql.

Применим условия равновесия плоской системы параллельных сил и составим два уравнения равновесия:

откуда R = ql + P = 210³ l,5 + 2 10³=5 10³ Н;

откуда т = Рl + ql²/2 = 2 10³ 1,5 + 2 10³ 2,25/2 = 5,25 10³ Н м.

Проверим решение, составив контрольное уравнение моментов относительно точки С:

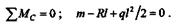
Подставив значения, получим

Полученное тождество 0 = 0 свидетельствует, что решение верное.

Пример 5.2. Предохранительный клапан А парового котла соединен стержнем АВ с однородным рычагом CD длиной SO см и силой тяжести 10 Н, который может вращаться вокруг неподвижной оси С; диаметр клапана d - 6 см, плечо СВ = 7 см (рис. 5.6). Какой груз G нужно подвесить к концу D рычага для того, чтобы клапан сам открывался при давлении в котле р = 110 Н/см²?

Решение. Рассмотрим равновесие рычага CD. Реакция R_B клапана будет направлена вверх и равна

Так как реакцию Re шарнира С определять не нужно, то составим уравнение моментов относительно точки С:

Подставим значения и определим G:

Пример 5.3. На рис. 5.7 схематически изображен подъемный кран. В точке D на расстоянии 5 м от оси АВ крана подвешен груз Р = 50 кН. Сила тяжести крана G = 30 кН. Определить реакции подпятника А и подшипника В.

Решение. Рассмотрим равновесие крана. Реакция R_B подшипника В направлена перпендикулярно его оси, реакцию подпятника А разложим на две составляющие: Х_A, и Y_A. Таким образом, к крану приложена плоская система пяти произвольно расположенных сил, из которых три неизвестны. Применим к этой системе аналитические условия равновесия и составим три уравнения:

Решая первое уравнение, получим

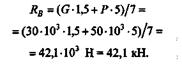
Из второго уравнения получим

Из третьего уравнения находим

Глава 6 ТРЕНИЕ

Понятие о трении

Абсолютно гладких и абсолютно твердых тел в природе не существует, и поэтому при перемещении одного тела по поверхности другого возникает сопротивление, которое называется трением. Трение — явление сопротивления относительному перемещению, возникающее между двумя телами в зонах соприкасания поверхностей по касательной к ним.

Трение — явление, чрезвычайно распространенное в природе и имеющее большое значение. На трении основана работа ременных и фрикционных передач, тормозных устройств, прокатных станов, наклонных транспортеров, фрикционных муфт и т. п. Трение обеспечивает сцепление с землей и, следовательно, работу автомобилей, тракторов и других транспортных машин. При отсутствии трения человек не мог бы ходить. Наряду с этим трение во многих случаях является вредным сопротивлением, на преодоление которого затрачивается нередко весьма большое количество энергии. Эти затраты энергии бесполезны и их стремятся уменьшить.

Приводим схему классификации трения по наличию и характеру движения.

Трением покоя называется трение двух тел при микросмещениях без

макросмещения {т. е. при малом относительном перемещении тел в

пределах перехода от покоя к относительному движению).

Трением движения называется трение двух тел, находящихся в относительном движении.

Далее рассмотрим виды трения в зависимости от наличия и характера относительного движения.

Трение скольжения

Трением скольжения называется трение движения, при котором скорости тел в точке касания различны по значению и (или)

направлению. Трение скольжения, как и трение покоя, обусловлено прежде всего шероховатостью и деформацией поверхностей, а также наличием молекулярного сцепления у прижатых друг к другу тел. Трение скольжения сопровождается изнашиванием, т. е. отделением или остаточной деформацией материала, а также нагревом трущихся поверхностей тел (остаточной называется деформация, не исчезающая после прекращения действия внешних сил). Трение характеризуется силой трения.

Сила трения есть сила сопротивления относительному перемещению двух тел при трении.

Возьмем тело, лежащее на горизонтальной шероховатой плоскости (рис 6.1). Сила тяжести G уравновешивается нормальной реакцией N. Если к телу приложить небольшую движущую силу Р, то оно не придет в движение, так как эта сила будет уравновешиваться силой трения F_тр, которая является, таким образом, реакцией опорной плоскости, направленной вдоль плоскости.

Если постепенно увеличивать сдвигающую силу Р, то до определенного ее значения тело будет оставаться в покое; при дальнейшем увеличении силы Р тело придет в движение.

Отсюда видно, что сила трения в состоянии покоя в зависимости от степени микросмещения может изменяться от нуля до какого-то максимального значения F , причем по модулю сила трения F_тр всегда равна сдвигающей силе Р(если Р не больше F).

Максимальное значение сила трения покоя имеет в момент начала относительного движения и называется наибольшей силой трения покоя или просто силой трения покоя.

Сила трения всегда направлена в сторону, противоположную направлению относительного движения тела.

В XVIII в. французские ученые Амонтон, а затем Кулон провели серьезные исследования в области трения и на основе их сформулировали три основных закона трения скольжения, обычно называемых законами Кулона:

1. Сила трения не зависит от величины площади трущихся поверхностей.

2. Максимальная сила трения прямо пропорциональна нормальной составляющей внешних сил, действующих на поверхности тела.

3. Сила трения зависит от материала тел, состояния трущихся поверхностей, наличия ирода смазки.

Первый закон можно подтвердить следующими соображениями. Если площадь трущихся поверхностей увеличится, то увеличится и количество сцепляющихся неровностей, но уменьшится давление (на единицу площади) и сопротивление относительному перемещению останется прежним.

Второй закон говорит о том, что если увеличится нормальная составляющая внешних сил, действующих на поверхности тела (иначе говоря, увеличится сила нормального давления или реакции), то во столько же раз возрастет максимальная сила трения.

Отношение силы трения F_тр к нормальной составляющей N внешних сил, действующих на поверхности тела, называется коэффициентом трения скольжения, обозначаемым f (при наибольшей силе трения покоя это отношение называется коэффициентом сцепления).

Таким образом,

(6.1)

В результате второй закон трения скольжения можно сформулировать так: сила трения равна коэффициенту трения скольжения, умноженному на силу нормального давления или реакции.

Очевидно, что коэффициент трения скольжения — величина безразмерная.

Нормальная реакция N опорной поверхности и сила трения F_тр дают равнодействующую R, которая называется полной реакцией опорной поверхности (рис. 6.1):

Полная реакция R составляет с нормалью к опорной поверхности какой-то угол. Максимальное значение этого угла (что будет в момент начала движения) называется углом трения и обозначается 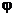. Из рис. 6.1 следует формула

(6.2)

Сравнивая равенства (6.1) и (6.2), получим

т. е. коэффициент трения скольжения равен тангенсу угла трения.

Если коэффициент трения скольжения одинаков для всех направлений движения, то множество (геометрическое место) полных реакций образует круговой конус, который называется конусом трения (рис 6.2). Если для разных направлений движения коэффициент трения

неодинаков (например, при скольжении по дереву вдоль и поперек волокон), то конус трения будет некруговым.

Свойство конуса трения заключается в том, что для равновесия тела, лежащего на шероховатой поверхности, равнодействующая приложенных к нему активных сил должна проходить внутри конуса трения.

По второму закону трения скольжения

Следовательно, при будет

Действительно, если равнодействующую Р активных сил, приложенных к телу, разложить на составляющие Р₁(движущая сила) и Р₂ (сила нормального давления), то

и движение окажется невозможным.

Согласно третьему закону, коэффициент трения скольжения зависит от материалов трущихся тел, качества обработки поверхностей, рода и температуры смазки.

В зависимости от наличия между сопрягаемыми поверхностями слоя смазки трение подразделяется на два вида: трение без смазочного материала и трение в условиях смазки.

Коэффициент трения скольжения определяют опытным путем: значения его для различных условий приведены в справочниках.

Приведем ориентировочные значения коэффициентов f трения скольжения (при покое):

Металл по металлу без смазки................... 0,15...0,3

То же, со смазкой........................................ 0,1...0,18

Дерево по дереву без смазки....................... 0,4...0,6

Кожа по чугуну без смазки......................... 0,3...0,5

То же, со смазкой ........................................ 0,15

Сталь по льду.............................................. 0,02

Коэффициент трения скольжения при движении обычно меньше, чем при покое, и в первом приближении не зависит от скорости относительного перемещения тел.

Методы решения задач статики при наличии трения остаются такими же, как и при отсутствии его, причем в уравнения равновесия обычно вводят максимальные значения сил трения.

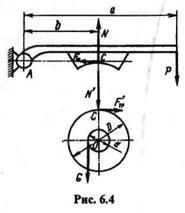
Пример 6.1.Диаметр шайбы колодочного тормоза D = 500 мм, диаметр барабана d = 100 мм, сила Р = 200 Н, груз G = 1500 Н, коэффициент трения f = 0,4 (рис. 6.3). Определить отношение размеров alb, при котором прекратится движение. Угол АСО — прямой.

Решение. В момент, когда движение прекратится, мысленно расчленим данную систему тел на две части и рассмотрим сначала равновесие барабана с шайбой, а затем равновесие рычага с колодкой (рис. 6.4). Согласно аксиоме взаимодействия, нормальная реакция N = N', а сила трения F_тр=F'_тр. На основании

второго закона трения скольжения равнодействующая сил трения колодки о шайбу равна

К обеим частям системы применим условие равновесия и составим два уравнения равновесия:

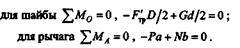
Решим полученную систему трех уравнений. Из первых двух уравнений найдем N:

Полученное выражение подставим в третье уравнение:

Отсюда определим отношение

Полученный результат минимален. Очевидно, что движения не будет при a/b 3,75.

Дата добавления: 2018-04-15; просмотров: 1261; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 5 6 7 8 91011 12 13 14 Следующая ⇒

Мы поможем в написании ваших работ!